隐马尔可夫模型（三）

预测算法

还记得隐马尔可夫模型的三个问题吗？本篇介绍第三个问题：预测问题，即给定模型参数和观测序列，求最有可能的状态序列，有如下两种算法。

近似算法

在每个时刻t选出当前最有可能的状态 i_t，从而得到一个状态序列。

给定隐马尔可夫模型参数 λ 和长度为T的观测序列O，在时刻 t 处于状态q_i的概率为

   (1)

其中使用了前向算法和后向算法，于是最有可能的状态的下表 i 为

                                    (2)

于是得到状态序列I^*=(i₁^*,i₂^*,...,i_T^*)

近似算法虽然计算简单，但是无法保证状态序列整体是最优的，也就是说在这个模型参数 λ 和观测序列O下，近似算法得到的状态序列可能不是出现概率最大的那个状态序列（即，P(I^*|O,λ) 可能不是最大值）

维特比算法

维特比算法实际使用了动态规划(dynamic programming)求概率最大路径（最优路径），这条路径就是这里的状态序列。

根据动态规划原理，如果最优路径在时刻 t 经过结点 i_t^*，那么从结点i_t^*到结点i_T^*之间的局部路径也是最优的。因为如果i_t^*到i_T^*之间如果有另一个更优的局部路径，那么将它与i₁^*到i_t^*之间的最优局部路径连接起来，就形成一条完整的更优路径，这与之前的最优路径矛盾。

上面这段话的意思是，到了时刻t，无论之前的局部路径选择如何，此后时刻t到时刻T之间的选择必须是最优的。

根据这一原理，我们可以从t=1时刻开始，递推计算在时刻t状态为 i 的各条局部路径的最大概率，这意味着最优局部路径经过结点 i_t^*。当t=T时的最大概率即为最优完整路径的概率，最优完整路径的终结点为i_T^*。因为我们计算的是在时刻 t 状态为 i 的局部概率，时刻t之前的各时刻状态不指定，这是为了减小计算量，在时刻 t 时，共计算 t * N 次概率，其中 N 为所有状态数。得到终结点i_T^*后，为了找到最优完整路径的其他结点，从终结点i_T^*开始，由后向前逐步求得节点i_T-1^*, ... , i₁^*。

引入两个变量

定义时刻 t 状态为i的所有局部路径(i₁,i₂,...,i_t)中概率最大值为

      (3)

即，指定 t 时刻的状态为 i，选择不同的状态组合(i₁,i₂,...,i_t-1)，使得上式中的概率最大，于是递推公式为，

 

令i_t=j，于是

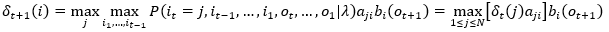   (4)

其中，

仔细研究δ_t(i)的含义，其实就是到达 t 时刻为止，观测序列已经确定为(o₁,o₂,...,o_t)，对应的状态序列(i₁,i₂,...,i_t)并且假设 i_t 的值为 i，O,I联合概率最大的值，设对应的状态为(i₁,i₂,...i_t=i)，于是这就是到达 t 时刻状态为 i 的局部最优路径，注意 限定了 t 时刻状态为 i。当t=T时，δ_T(i)就是状态为 i 的O,I联合概率最大值，那么假设 i = m 时δ_T(i)值达到最大，那么状态序列(i₁,i₂,...,i_T-1,i_T=m)就是所求的最有可能出现的状态序列。

好了，给出下图，进行一些可能是无用（然而我就是喜欢啰嗦，摊手~）的分析：

如图，横轴方向表示时刻 t，纵轴方向表示状态 i，结点之间的箭头表示转移，结点(t,j)对应的局部最优概率为δ_t(j)，那么从时刻 t 转移到 时刻 t+1时，如果时刻 t+1 的状态为 i，那么时刻 t 的状态可以是 1<=j<=N，这N个状态到底使用哪个状态呢，不难想到，对时刻 t 来说，某个状态 j 的局部最优概率为δ_t(j)，状态 j 到 状态 i 的转移概率为 a_ji，自然地，我们对 1<= j<=N，寻找 δ_t(j)*a_ji的最大值，比如图中那个红色的箭头对应δ_t(j)*a_ji的最大值，t 时刻其他状态转移到 t+1 时刻的 i 状态的箭头全被否定掉，如图中叉叉掉的箭头（注意仅叉掉 到(t+1,i)的结点的连线，到 t+1 时刻其他状态的结点不能这么贸然叉掉，而是同 i 状态下一样的选择）。这样再乘以一个与 t 时刻状态 j 无关的一个值 b_i(o_t+1)（也就是说无论 t 时刻选择什么状态，这个值都不变），就得到δ_t+1(i)，那么当 t+1 = T 时，即最终时刻，只要遍历一下 t+1 时刻的所有状态 i，找出 max(δ_t+1(i)) 对应的那个 i 的值就就是完整的最优路径的终结点 (T,i)。倒过来推，那么δ_t(j)是如何确定的呢？显然类似地，选择结点(t-1,k)，使得 δ_t-1(k)*a_t-1,t 的值最大，于是就这样一直倒推，直到起始时刻 1，而我们知道 δ₁(i)=π_ib_i(o₁)。

假设我们每个时刻每个状态形成一个结点，那么每个结点的局部最优概率形成的路线也许就是下图这个样子，

也就是每个结点都有对应的局部最优概率值，且由上一时刻的某个状态转移过来。而上一时刻某个状态的结点也可能转移到下一时刻的多个状态结点。

好吧，费话了一大篇，还不知道讲清楚没，悲催~

定义时刻 t 的状态为 i 的所有局部路径(i₁,i₂,...,i_t)中概率最大值对应的那个局部路径的第 t-1 个结点为

                           (5)

即，第 t-1 个结点为 i_t-1^*，t-1时刻的状态就是使上式值最大对应的那个状态下标 j。

为什么这么做就可以呢？

再次看一下上面的那个图，因为图中两相邻时刻标记的是 t 和 t+1 时刻，我就使用图中的标记，其实本质是一样的。

看一下图，从 t 到 t+1 的状态，我们选择的是什么样的转移（什么样的红色箭头）？已知 t+1 时刻的状态为 i，那么转移的选择是根据 δ_t(j)*a_ji 的最大值选择的，其中 j 表示 t 时刻的某个状态，自然要求使得 δ_t(j)*a_ji 最大所对应的那个 j 作为 t 时刻的状态，依次逆推下去，直到 t = 1，得到第一个观测状态，如此，形成我们要求的概率最大的状态序列。

实际在程序中，上述的这种逆推其实并不需要真正地逆推，只要在递推计算δ_t(i)的时候，将 max[δ_t-1(j)a_ji] 所对应的那个 j 值保存到一个状态下标的列表中即可。

ref

统计学习方法，李航

代码

可参考jieba分词