最近学习了极客时间的《数据结构与算法之美》很有收获,记录总结一下。
欢迎学习老师的专栏:数据结构与算法之美
代码地址:https://github.com/peiniwan/Arithmetic
树
树是无向、连通的无环图。


“高度”这个概念,其实就是从下往上度量,比如我们要度量第 10 层楼的高度、第 13 层楼的高度,起点都是地面。所以,树这种数据结构的高度也是一样,从最底层开始计数,并且计数的起点是 0。
“深度”这个概念在生活中是从上往下度量的,比如水中鱼的深度,是从水平面开始度量的。所以,树这种数据结构的深度也是类似的,从根结点开始度量,并且计数起点也是 0。
“层数”跟深度的计算类似,不过,计数起点是 1,也就是说根节点的位于第 1 层。
二叉树
如何表示(或者存储)一棵二叉树
一种是基于指针或者引用的二叉链式存储法
一种是基于数组的顺序存储法。
链式存储法
每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要拎住根节点,就可以通过左右子节点的指针,把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
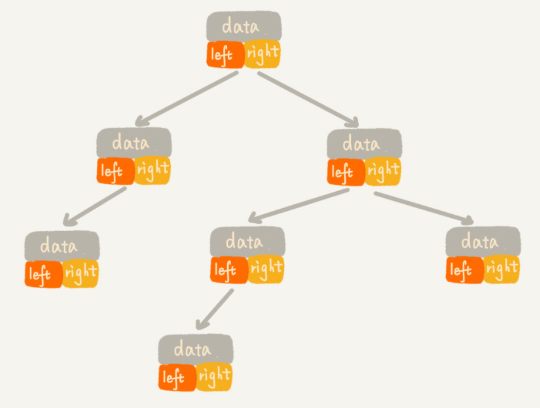
基于数组的顺序存储法
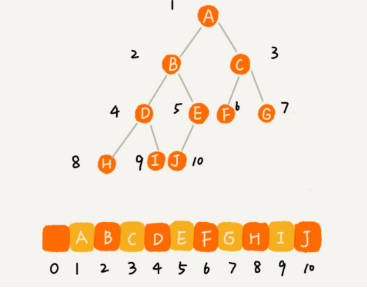
把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
二叉树的遍历
前序遍历、中序遍历和后序遍历
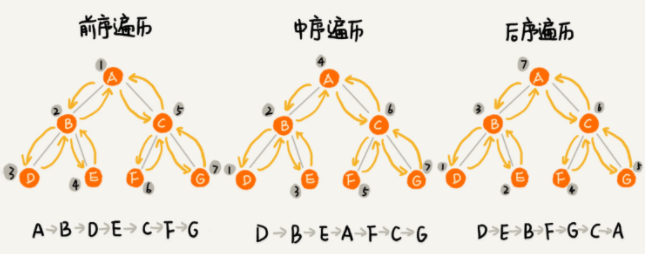
写递归代码的关键,就是看能不能写出递推公式,而写递推公式的关键就是,如果要解决问题 A,就假设子问题 B、C 已经解决,然后再来看如何利用 B、C 来解决 A。所以,我们可以把前、中、后序遍历的递推公式都写出来。
二叉树遍历的时间复杂度
从我前面画的前、中、后序遍历的顺序图,可以看出来,每个节点最多会被访问两次,所以遍历操作的时间复杂度,跟节点的个数 n 成正比,也就是说二叉树遍历的时间复杂度是 O(n)。
二叉查找树(Binary Search Tree)
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
叉查找树最大的特点就是,支持动态数据集合的快速插入、删除、查找操作。不需要有序
1. 二叉查找树的查找操作
public class BinarySearchTree {
private Node tree;
public Node find(int data) {
Node p = tree;
while (p != null) {
if (data < p.data) p = p.left;
else if (data > p.data) p = p.right;
else return p;
}
return null;
}
}
2. 二叉查找树的插入操作
二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。
public void insert(int data) {
if (tree == null) {
tree = new Node(data);
return;
}
Node p = tree;
while (p != null) {
if (data > p.data) {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
} else { // data < p.data
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
二叉查找树的时间复杂度分析
中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
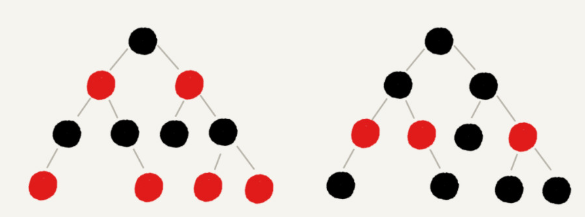
看图2
查找、插入、删除等很多操作的时间复杂度都跟树的高度成正比

图中第一种二叉查找树,根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了 O(n)。
我们现在来分析一个最理想的情况,二叉查找树是一棵完全二叉树(或满二叉树)。这个时候,插入、删除、查找的时间复杂度是多少呢?
从我前面的例子、图,以及还有代码来看,不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是 O(height)。既然这样,现在问题就转变成另外一个了,也就是,如何求一棵包含 n 个节点的完全二叉树的高度?
树的高度就等于最大层数减一,为了方便计算,我们转换成层来表示。从图中可以看出,包含 n 个节点的完全二叉树中,第一层包含 1 个节点,第二层包含 2 个节点,第三层包含 4 个节点,依次类推,下面一层节点个数是上一层的 2 倍,第 K 层包含的节点个数就是 2^(K-1)。
平衡二叉查找树的高度接近 logn,所以插入、删除、查找操作的时间复杂度也比较稳定,是 O(logn)。
二叉查找树和散列表
散列表的插入、删除、查找操作的时间复杂度可以做到常量级的 O(1),非常高效。而二叉查找树在比较平衡的情况下,插入、删除、查找操作时间复杂度才是 O(logn),相对散列表,好像并没有什么优势,那我们为什么还要用二叉查找树呢?
第一,散列表中的数据是无序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
第二,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。
第三,笼统地来说,尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
第四,散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
最后,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。
红黑树
平衡二叉查找树
平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于 1。从这个定义来看,上一节我们讲的完全二叉树、满二叉树其实都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树。

很多平衡二叉查找树其实并没有严格符合上面的定义(树中任意一个节点的左右子树的高度相差不能大于 1),比如我们下面要讲的红黑树,它从根节点到各个叶子节点的最长路径,有可能会比最短路径大一倍。
平衡二叉查找树中“平衡”的意思,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些,相应的插入、删除、查找等操作的效率高一些。
AVL树不存在变色的问题,只有左旋转、右旋转这两种操作。
如何定义一棵“红黑树”?
新加入的就是红节点
漫话
红黑树的英文是“Red-Black Tree”,简称 R-B Tree。
顾名思义,红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
这里的第二点要求“叶子节点都是黑色的空节点”,稍微有些奇怪,它主要是为了简化红黑树的代码实现而设置的,下一节我们讲红黑树的实现的时候会讲到。这节我们暂时不考虑这一点,所以,在画图和讲解的时候,我将黑色的、空的叶子节点都省略掉了。
为什么说红黑树是“近似平衡”的?
平衡二叉查找树的初衷,是为了解决二叉查找树因为动态更新导致的性能退化问题。所以,“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重。
红黑树的高度不是很好分析,我带你一步一步来推导。
首先,我们来看,如果我们将红色节点从红黑树中去掉,那单纯包含黑色节点的红黑树的高度是多少呢?
红色节点删除之后,有些节点就没有父节点了,它们会直接拿这些节点的祖父节点(父节点的父节点)作为父节点。所以,之前的二叉树就变成了四叉树。
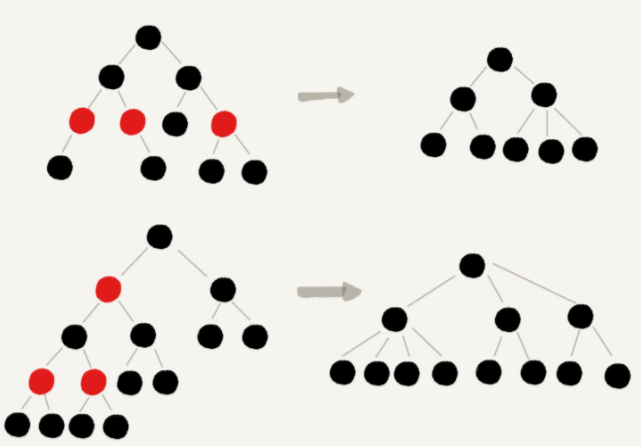
前面红黑树的定义里有这么一条:从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。我们从四叉树中取出某些节点,放到叶节点位置,四叉树就变成了完全二叉树。所以,仅包含黑色节点的四叉树的高度,比包含相同节点个数的完全二叉树的高度还要小。
完全二叉树的高度近似 log2n,这里的四叉“黑树”的高度要低于完全二叉树,所以去掉红色节点的“黑树”的高度也不会超过 log2n。
我们现在知道只包含黑色节点的“黑树”的高度,那我们现在把红色节点加回去,高度会变成多少呢?
从上面我画的红黑树的例子和定义看,在红黑树中,红色节点不能相邻,也就是说,有一个红色节点就要至少有一个黑色节点,将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过 log2n,所以加入红色节点之后,最长路径不会超过 2log2n,也就是说,红黑树的高度近似 2log2n。
所以,红黑树的高度只比高度平衡的 AVL 树的高度(log2n)仅仅大了一倍,在性能上,下降得并不多。这样推导出来的结果不够精确,实际上红黑树的性能更好。
为什么工程中都喜欢用红黑树,而不是其他平衡二叉查找树呢?
AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是,有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。
红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。
红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中,复杂度退化的问题而产生的。红黑树的高度近似 log2n,所以它是近似平衡,插入、删除、查找操作的时间复杂度都是 O(logn)。
递归树分析算法复杂度
借助递归树来分析递归算法的时间复杂度。
递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解为小小问题。这样一层一层地分解,直到问题的数据规模被分解得足够小,不用继续递归分解为止。
如果我们把这个一层一层的分解过程画成图,它其实就是一棵树。我们给这棵树起一个名字,叫作递归树。
递归树与时间复杂度分析
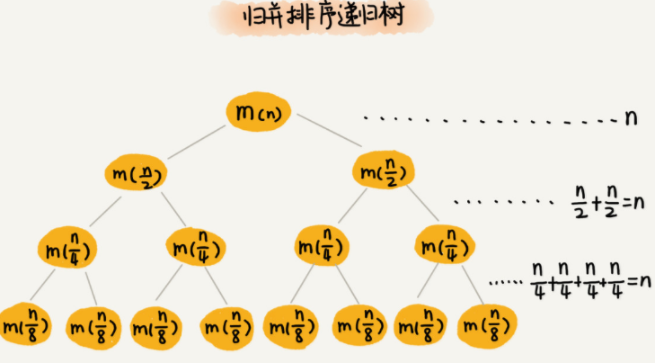
每一层归并操作消耗的时间总和是一样的,跟要排序的数据规模有关。我们把每一层归并操作消耗的时间记作 n。
现在,我们只需要知道这棵树的高度 h,用高度 h 乘以每一层的时间消耗 n,就可以得到总的时间复杂度 O(n∗h)。
归并排序递归树是一棵满二叉树。我们前两节中讲到,满二叉树的高度大约是 log2n,(第 K 层包含的节点个数就是 2^(K-1))
所以,归并排序递归实现的时间复杂度就是 O(nlogn)。
接下来我会通过三个实际的递归算法,带你实战一下递归的复杂度分析。学完这节课之后,你应该能真正掌握递归代码的复杂度分析。
实战一:分析快速排序的时间复杂度
我们还是取 k 等于 9,也就是说,每次分区都很不平均,一个分区是另一个分区的 9 倍。如果我们把递归分解的过程画成递归树,就是下面这个样子:
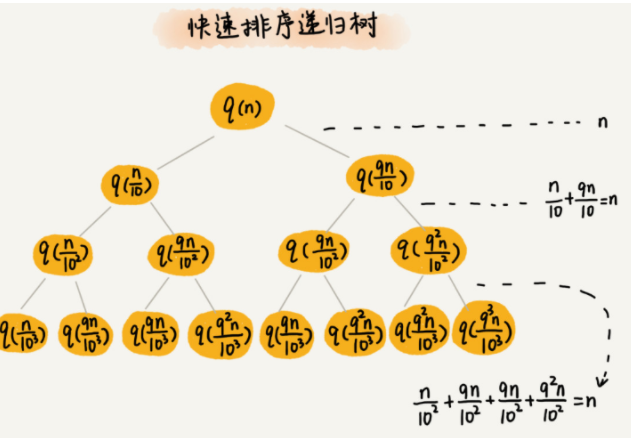
排序的过程中,每次分区都要遍历待分区区间的所有数据,所以,每一层分区操作所遍历的数据的个数之和就是 n。我们现在只要求出递归树的高度 h,这个快排过程遍历的数据个数就是 h∗n ,也就是说,时间复杂度就是 O(h∗n)。
实战二:分析斐波那契数列的时间复杂度
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}
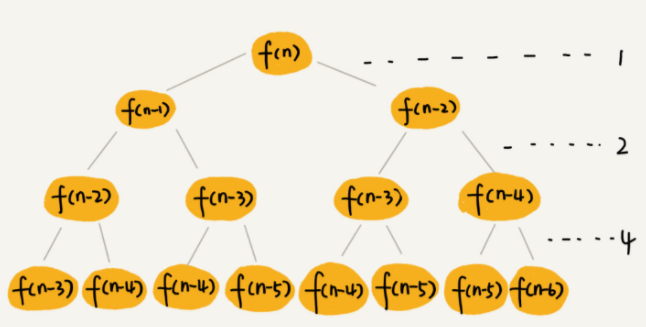
每次分解之后的合并操作只需要一次加法运算,我们把这次加法运算的时间消耗记作 1。所以,从上往下,第一层的总时间消耗是 1,第二层的总时间消耗是 2,第三层的总时间消耗就是 2^n。依次类推,第 k 层的时间消耗就是 2^k−1,那整个算法的总的时间消耗就是每一层时间消耗之和。
如果路径长度都为 n,那这个总和就是 2^n−1。

这个算法的时间复杂度就介于上面之间。虽然这样得到的结果还不够精确,只是一个范围,但是我们也基本上知道了上面算法的时间复杂度是指数级的,非常高。
实战三:分析全排列的时间复杂度
如何把 n 个数据的所有排列都找出来
如果我们确定了最后一位数据,那就变成了求解剩下 n−1 个数据的排列问题。而最后一位数据可以是 n 个数据中的任意一个,因此它的取值就有 n 种情况。所以,“n 个数据的排列”问题,就可以分解成 n 个“n−1 个数据的排列”的子问题。
假设数组中存储的是1,2, 3...n。
f(1,2,...n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +...+{最后一位是n, f(n-1)}。
// 调用方式:
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k表示要处理的子数组的数据个数
public void printPermutations(int[] data, int n, int k) {
if (k == 1) {
for (int i = 0; i < n; ++i) {
System.out.print(data[i] + " ");
}
System.out.println();
}
for (int i = 0; i < k; ++i) {
int tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
printPermutations(data, n, k - 1);
tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
}
}

堆排序
- 堆排序是利用堆这种数据结构而设计的一种排序算法,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。一般升序采用大顶堆,降序采用小顶堆。
- 堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
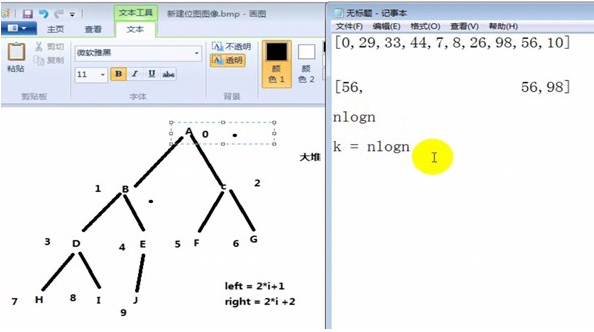
public class HeapSort {
public static void main(String[] args) {
HeapSort heapSort = new HeapSort();
int[] array = {19, 8, 27, 6, 35, 14, 3, 12, 1, 0, 9, 10, 7};
//{35, 8, 27, 6, 19, 14, 3, 12, 1, 0, 9, 10, 7}
System.out.println("Before heap:");
heapSort.printArray(array);
heapSort.heapSort(array);
System.out.println("After heap sort:");
heapSort.printArray(array);
}
//(1)
public void heapSort(int[] array) {
buildMaxHeap(array);//建立最大堆
for (int i = array.length - 1; i >= 1; i--) {
//最大的在0位置,那么开始沉降,这样每交换一次最大的值就丢到最后了
exchangeElements(array, 0, i);
//继续获取0位置最大值,将第一次排序后到了最后面的最大值排除
//重新调整结构,使其满足堆,然后继续交换堆顶元素与当前末尾元素,
//反复执行调整+交换步骤,直到整个序列有序。
maxHeap(array, i, 0);
}
}
//(2)建立最大堆
private void buildMaxHeap(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int half = (array.length - 1) / 2;//从一半开始,6
for (int i = half; i >= 0; i--) {
maxHeap(array, array.length, i);
}
}
private void maxHeap(int[] array, int heapSize, int index) {//index堆头
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
//三者找最大值
if (left < heapSize && array[left] > array[index]) {
largest = left;
}
if (right < heapSize && array[right] > array[largest]) {
largest = right;
}
if (index != largest) {
exchangeElements(array, index, largest);
//继续构造下面的大堆
maxHeap(array, heapSize, largest);
}
}
//(3)换位置
public void exchangeElements(int[] array, int index1, int index2) {
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
public void printArray(int[] array) {
System.out.print("{");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]);
if (i < array.length - 1) {
System.out.print(", ");
}
}
System.out.println("}");
}
}