在处理非平稳、非线性的信号时,常用的方法是小波分解(wavelet decomposition)的方法。后来一种以数据驱动的经验模态分解(Empirical Mode Decompesotion, EMD)方法被提出,它能够将非平稳信号分解成不同的本征模函数(IMF)。相比于小波分解,它虽然不会受小波基函数的选择,分解等级等影响,但是它也存在很多问题。其中混叠模态就是其中之一。
混叠模态问题最先在对含有间断的信号分解中发现的。 间断信号可以理解为在某一时刻或者某一很小时间间隔内出现了小幅值的高频信号。当混叠模态出现时,得到的本征模函数(IMF)是没有意义的。在 ZHAOHUA WU and NORDEN E. HUANG 的文章中,混叠模态是这么定义的:
“Mode mixing” is defined as any IMF consisting of oscillations of dramatically disparate scales, often caused by intermittency of the driving mechanisms.
指的是在一个本征模函数(IMF)中包含差异极大的特征时间尺度,或者相近的特征时间尺度分布在不同的本征模函数(IMF)中。
在wu的文章中举了一个例子,输入信号是一个在连续低频正弦信号上叠加了间歇性高频震动的调制信号(the modeled data was a mixture of intermittent highfrequency oscillations riding on a continuous low-frequency sinusoidal signal)。下图直接出自原文。
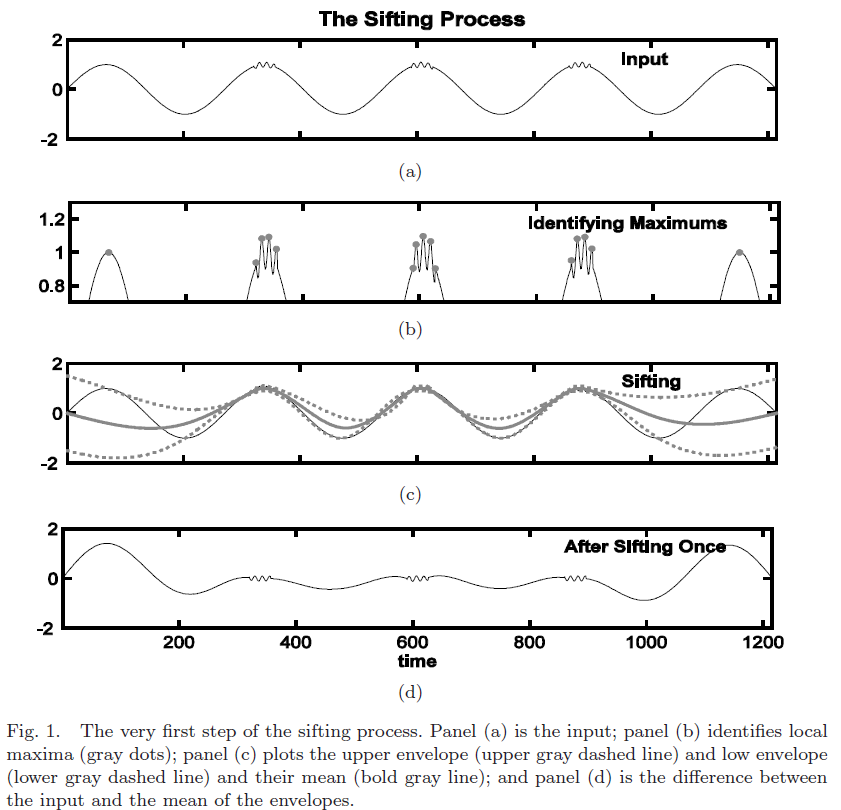
这里图示的是怎么求第一阶本征模函数(IMF)。步骤是先对原始信号(a)的求局部的极值(b),然后通过插值的方式插出上包络线和下包络线,在求上下包络线每一时刻对应的平均值(c),最后判断上一步得到的平均值是否满足本征模函数(IMF)成立的条件。如果满足则确定为一个本征模函数(IMF)。如果不满足则把得到的平均值数列当做原始信号依次进行(a)(b)(c),直到满足本征模函数(IMF)的条件。
从上面的分解过程也能知道,混叠模态问题实质是由经验模分解的过程中因为局部极值在很短的时间间隔内发生多次跳变导致的。基本上数据都掺杂着噪声或者我们不知道的间断信号,为了解决这个问题,wu最早提出的解决方法是集合模态分级法(Ensemble Empirical Mode Decomposition,EEMD). 这里的集合可以理解为集合平均。
集合模态分级法(Ensemble Empirical Mode Decomposition,EEMD)是一种噪声协助分析方法(Noise-Assisted Data Analysis),不过要注意的是添加了噪声会降低信号的信噪比。分解步骤如下:
(1)对原始信号添加白噪声; (2)分解(1)中得到的信号; (3)重复(1)(2)步骤,得到本征模函数(IMF)。每次(1)中加的白噪声新产生的; (4)最后求多个对应的本征模函数(IMF)的平均值作为最后的结果。
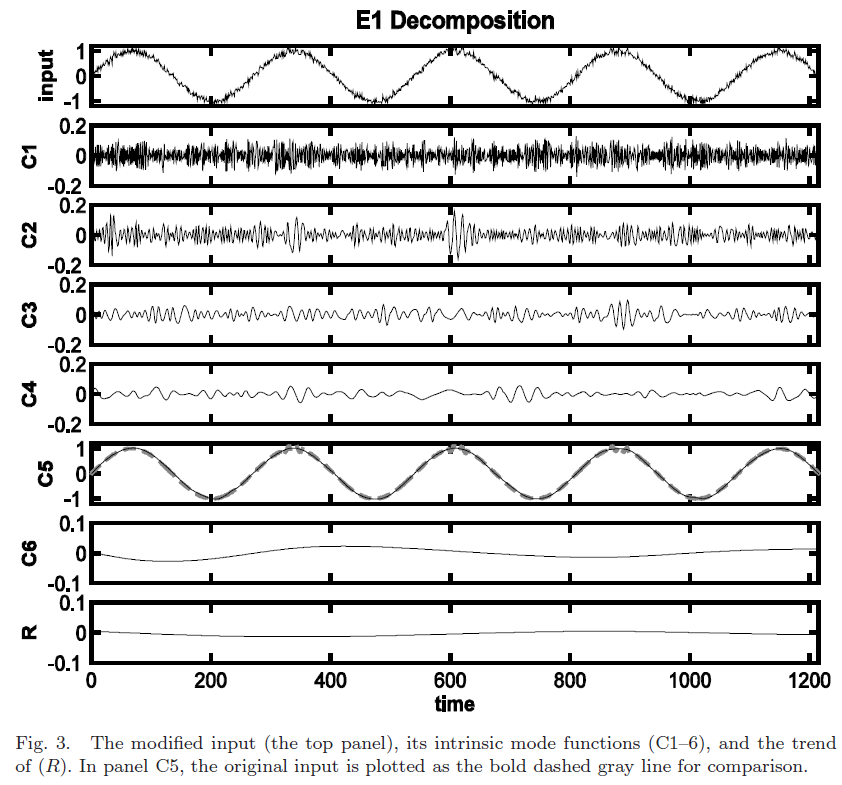
下面是集合模态分级法(Ensemble Empirical Mode Decomposition,EEMD)分解的示例,使用与上图1相同的信号。结果也直接取自Wu的文章。说起来简单,但是要注意的事项也比较多,比如加了噪声后对信号的影响,加多大的噪声等。Wu的文章添加的是标准差为0.1的噪声。
从上图可以看到高频的间断信号被噪声淹没了,低频信号基本完美地被提取出来。随着集合次数的增加,高频间断信号会变得越来越小。