CS61A Efficiency 笔记

CS61A Spring 学习笔记
原文地址： http://composingprograms.com/pages/28-efficiency.html

Measuring Efficiency

计算一个程序需要多长时间和多少的内存是很困难的。一个可行的方式就是计算一个事件比如一个函数被调用了多少次。
比如Fibonacci数列

>>> def fib(n):
        if n == 0:
            return 0
        if n == 1:
            return 1
        return fib(n-2) + fib(n-1)

比如我们计算fib(6)
因为递归，所以每次计算都要重复调用更小的fib(x)，导致很多冗余计算。
定义一个计算某个函数被调用了多少次的高阶函数。这个函数的返回一个与输出等效函数，还包含一个计数用的变量。

>>> def count(f):
        def counted(*args):
            counted.call_count += 1
            return f(*args)
        counted.call_count = 0
        return counted

example 1:https://goo.gl/L6Ee3T

def count(f):
    def counted(*args):
        counted.call_count += 1
        return f(*args)
    counted.call_count = 0
    return counted

def test(n):
    if n<=3:
        return 1
    else: 
         return test(n-2)+test(n-4)+1

test = count(test)
ret = test(8)
c = test.call_count

example2:https://goo.gl/D8cxm5

def count(f):
    def counted(*args):
        counted.call_count += 1
        return f(*args)
    counted.call_count = 0
    return counted

def fib(n):
        if n == 0:
            return 0
        if n == 1:
            return 1
        return fib(n-2) + fib(n-1)

fib = count(fib)
ret = fib(6)
c = fib.call_count

Space

想知道函数占用多少的空间。我们需要知道函数执行过程中如何使用，保留和回收内存。如果一个环境为正在执行的部分提供上下文，那么我们说这个环境是激活的。当函数最终调用了return，函数不再是激活的。
在下面的执行过程中，当执行完成后，相应的环境(frame)不再需要时会变成灰色，表示不再激活。当return的返回值好没有被执行，对应的那个frame始终是激活的。
这里定义了一个高阶函数去计算最多同时有多少个frame被激活。

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n-2) + fib(n-1)

def count_frames(f):
        def counted(*args):
            counted.open_count += 1
            counted.max_count = max(counted.max_count, counted.open_count)
            result = f(*args)
            counted.open_count -= 1
            return result
        counted.open_count = 0
        counted.max_count = 0
        return counted

fib = count_frames(fib)
fib(4)

https://goo.gl/vLsjiU

Memoization

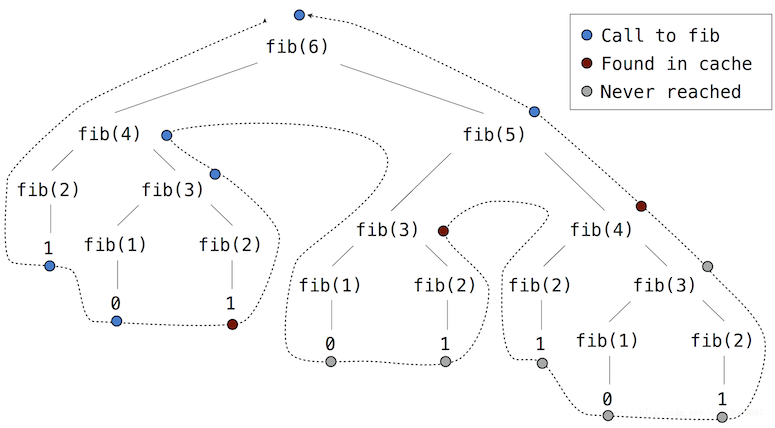
在树回归中，像上面求解斐波那契数列的时候，很多次重复的计算是没有必要的。使用记忆化就能够把曾经计算过的结果用cache保存起来，在遇到相同的参数时，只需按照参数在cache中索引相应的值即可。这样做能够大大提高运算的效率。
记忆化使用一个高阶函数来表达，它也可以作为一个装饰器(decorator)。

>>> def memo(f):
        cache = {}
        def memoized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memoized

计算的过程由下图可以观察到

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n-2) + fib(n-1)

def count(f):
        def counted(*args):
            counted.call_count += 1
            return f(*args)
        counted.call_count = 0
        return counted 

def memo(f):
    cache = {}
    def memoized(n):
        if n not in cache:
            cache[n] = f(n)
        return cache[n]
    return memoized       

counted_fib = count(fib)
fib  = memo(counted_fib)
fib(5)

counted_fib.call_count

fib(6)

counted_fib.call_count

https://goo.gl/NQDRvj

Orders of Growth

影响函数执行时的space和time的因素很多，很难求得实际中使用了多少。为方便估算，把不同类型的计算按照不同的复杂度划分类别。
使用Θ$\mathrm{\Theta }$标注：
n 表示输入的规模
R(n)$R(n)$表示n为输入时需要的资源
我们称R(n)$R(n)$有Θ(f(n))$\mathrm{\Theta }(f(n))$的计算数量级增长(order of growth)，写作R(n)=Θ(f(n))$R(n)=\mathrm{\Theta }(f(n))$.
存在一个上界和一个下界k1$k_1$,k2$k_2$，使得

k1⋅f(n)≤R(n)≤k2⋅f(n)$$k_1\cdot f(n)\le R(n)\le k_2\cdot f(n)$$

Example: Exponentiation

使用递归计算 bn$b^n$

>>> def exp(b, n):
        if n == 0:
            return 1
        return b * exp(b, n-1)

这是一个线性递归过程，需要 Θ(n)$\mathrm{\Theta }(n)$步和 Θ(n)$\mathrm{\Theta }(n)$ space.
另外一个计算方式：

>>> def exp_iter(b, n):
        result = 1
        for _ in range(n):
            result = result * b
        return result

使用连续乘方计算：

b2b4b8=b⋅b=b2⋅b2=b4⋅b4$$\begin{array}{rl}{b}^2& =b\cdot b\\ b^4& =b^2\cdot b^2\\ b^8& =b^4\cdot b^4\end{array}$$

这时只需要计算3步，但是这种方法使用于幂是2的情况。改进这个连续乘方的方法使其适用于任何幂。

bn={(b12n)2b⋅bn−1if n is evenif n is odd$$b^n=\{\begin{array}{ll}(b^{\frac{1}{2}n}{)}^2& \text{if }n\text{ is even}\\ b\cdot b^{n-1}& \text{if }n\text{ is odd}\end{array}$$

>>> def square(x):
        return x*x
>>> def fast_exp(b, n):
        if n == 0:
            return 1
        if n % 2 == 0:
            return square(fast_exp(b, n//2))
        else:
            return b * fast_exp(b, n-1)
>>> fast_exp(2, 100)
1267650600228229401496703205376

https://goo.gl/fYPkf8

这个快速的算法是计算的复杂度降为Θlog(n)$\mathrm{\Theta }log(n)$，当n取值很大的时候，它跟Θ(n)$\mathrm{\Theta }(n)$的区别就很明显。如n=1000时，上面的算法计算只需要执行14次乘法，而不是1000次。

Growth Categories

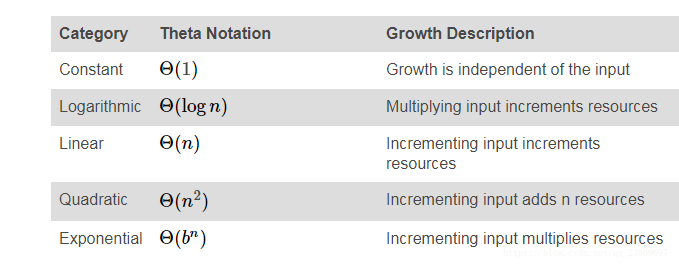
常见计算复杂度的分类：
1) 常数项
这两个的复杂度是相同的。
Θ(n)$\mathrm{\Theta }(n)$ = Θ(500∗n)$\mathrm{\Theta }(500\ast n)$
2) 对数
对数的底的取值对复杂度没有影响
3) 嵌套

>>> def overlap(a, b):
        count = 0
        for item in a:
            if item in b:
                count += 1
        return count

复杂度为Θ(m⋅n)$\mathrm{\Theta }(m\cdot n)$, m 外循环的长度，n为内循环的长度。
4）低阶项
比如下面的例子，两个数列中一个相差为1的组合有多少？

def overlap(a, b):
    count = 0
    for item in a:
        if item in b:
            count += 1
    return count

def one_more(a):
    return overlap([x-1 for x in a], a)

one_more([3, 14, 15, 9])

https://goo.gl/kYLbne
这里的复杂度为Θ(n+n2)$\mathrm{\Theta }(n+n^2)$,其中n为列表的长度

常见的分类：