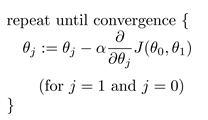【吴恩达机器学习笔记】线性回归模型之单变量线性回归

文章目录

• 1.机器学习概览
• 1.1 监督学习
• 1.1.1 回归问题：预测连续值
• 1.1.2 分类问题：预测离散值(二分类、多分类)
• 1.2 无监督学习
• 1.3 其他
• 1.4 机器学习一般过程
• 2.单变量线性回归模型(Linear Regression with One Variable)
• 2.1 假设函数(Hypothesis function)
• 2.2 代价函数(Cost function)
• 2.3 优化目标(目标函数)
• 2.4 批量梯度下降法(Batch Gradient Descent Algorithm)

1.机器学习概览

1.1 监督学习

教机器进行学习，数据集有标签，主要有：

1.1.1 回归问题：预测连续值

以线性回归为例，主要有：

• 单变量线性回归
• 多变量线性回归
• 多项式回归

1.1.2 分类问题：预测离散值(二分类、多分类)

以二分类为例，主要有：

• 逻辑回归(Logistic Regression)算法/模型(该模型的输出变量范围始终在0和1之间)

1.2 无监督学习

让机器自己学习，数据集无标签，主要有：

• 聚类问题
• 鸡尾酒会问题
• 其他

1.3 其他

• 强化学习
• 推荐系统

1.4 机器学习一般过程

$Training Set \ downarrow \$
$Learning Algorithm \ downarrow$
$Size of house o h o Estimated price$

2.单变量线性回归模型(Linear Regression with One Variable)

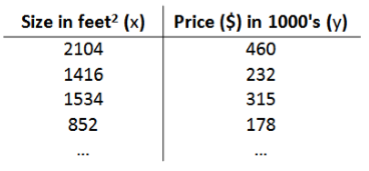
以根据房屋面积预测房价为例对该模型进行解释，训练集如下：

顾名思义，单变量线性回归即模型中只有一个自变量的回归模型，也即研究的问题中只有一个特征变量，这里我们的特征变量就是房屋的面积，详细解释如下。

2.1 假设函数(Hypothesis function)

$h_{θ}(x) = θ_{0} + θ_{1}x$

注：$θ_i$(i=0,1)(记作θ)称为模型参数(parameters)，对于固定的$θ$，假设函数是一个关于x的函数。我们最终的目标是根据训练样本的数据，求出合适的$θ$的值来拟合我们的数据。

2.2 代价函数(Cost function)

$J(θ_{0},θ_{1}) = frac{1}{2m}sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})^2$
注：代价函数是一个关于模型参数(即$θ$)的函数。m表示训练数据集中样本的个数，$x^{(i)}$表示特征x在第i个样本的取值，$y^{(i)}$表示标签y在第i个样本的取值，如在上图数据集中$x^{(1)}$=2104，$y^{(1)}$=460。

2.3 优化目标(目标函数)

$minimize_{(θ_{0},θ_{1})}J(θ_{0},θ_{1})$
有了优化的目标，那么找到能使$J(θ_{0},θ_{1})$最小化的参数θ即可，方法有梯度下降法或者正规方程法(后面详细解释)。

2.4 批量梯度下降法(Batch Gradient Descent Algorithm)

Batch：Each step of gradient descent use all the training examples.即批梯度下降法每次更新参数θ都使用全部的训练样本数据，看下面梯度下降更新公式的向量形式及向量形式前面的更新公式就可以明白 。

用来最小化代价函数$J(θ_{0},θ_{1})$的方法，一般可以最小化任意代价函数，不止是线性回归的代价函数。公式如下：

需要注意的两点：
(1)$θ_{0},θ_{1}$要同步更新(Simultaneous update)，即:

$temp0 = θ_{0} - α fracpartial{partial θ_{0}}J(θ_{0},θ_{1})$
$temp1 = θ_{1} - α fracpartial{partial θ_{1}}J(θ_{0},θ_{1})$

$θ_{0} = temp0$
$θ_{1} = temp1$
(2)α称为学习速率(learning rate)

(3)$J(θ_{0},θ_{1})$需要为凸函数(Convex function)

为了便于进行向量化的运算，在训练数据集的第一列插入一列值全为1的特征，即$x_{0}^{(i)}$=1，则假设函数变为：
$h_{θ}(x) = θ_{0} + θ_{1}x = θ_{0}x_{0} + θ_{1}x_1$
从而代价函数变为：
$J(θ_{0},θ_{1}) = frac{1}{2m}sum_{i=1}^{m}(θ_{0}x_{0} ^{(i)}+ θ_{1}x_1^{(i)}-y^{(i)})^2$

将此假设函数、代价函数代入到梯度下降法的更新公式中，则有：
repeat until convergence{
$θ_{j} = θ_{j} - α frac{1}{m}sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})x_{j}^{(i)}$}(for j=0 and j=1)
进一步将梯度下降更新公式写成向量形式：
repeat until convergence{
$θ_{j} = θ_{j} - α frac{1}{m}(Xθ-vec y)x_j$ }
其中，$X = egin{bmatrix} cdots & (x^{(1)})^T & cdots \ cdots & (x^{(2)})^T & cdots \ & vdots & \ cdots & (x^{(m)})^T & cdots end{bmatrix}, qquad vec y = egin{bmatrix} y^{(1)} \ y^{(2)} \ vdots \ y^{(m)} end{bmatrix}$,$x^{(i)}$为列向量，X为m*(n+1)维的矩阵，$vec y$、$x_j$为m维列向量，θ为(n+1)维的列向量。

向量形式的更新公式更便于梯度下降法的编程实现。