dijkstra:计算图的最短路径。
相关代码:
test_dijkstra.m:实现了dijkstra算法,生成一个20*20的网格,分别对网格的边赋予权值。然后从序号为200的顶点出发到达序号为90的顶点。最终得到的结果为找到序号90的顶点的路径。调用了gen_square_graph,preform_dijkstra,perform_dijkstra_path_extraction,plot_dijkstra方法,分别实现生成m*m的图,dijkstra算法,提取路径和显示。
gen_square_graph.m:生成边为n的图。源自http://www.mathworks.com/matlabcentral/fileexchange/5355-toolbox-graph/content/toolbox_graph/load_graph.m
function [A,xy] = gen_square_graph( n, connectivity )
参数说明:n——生成的图的边的长度;
connectivity——默认为4,也就是{[-1,0], [1,0], [0,1], [0,-1]}中的点构成的正方形;
设定为8时,倾斜方向也可以相连。
输出:A——n^2*n^2的邻接矩阵,记录顶点间的连接关系。
xy——n^*2的矩阵,记录顶点的位置信息。(其中n为上面的参数n,而非顶点个数,顶点个数为n^2)
preform_dijkstra.m:实现dijkstra算法。主要思想为找到从起始点到所有其他顶点的最短距离。为稀疏矩阵提供更加快捷的实现方法:perform_dijkstra_fast。
function [D,S] = perform_dijkstra(W, start_points, options)
参数说明:W——权重矩阵,W(i,j)表示从i顶点到j顶点之间的距离。
start_points——起始点。
options——end-points:设定终点。
use_mex:是否使用C语言产生的mex文件。
输出:D——n^2*1的向量,记录到起点的距离
S——描述状态,dead = -1,open = 0,far = 1.也就是说已到达顶点为-1,即将到达顶点为0,为到达顶点为1(为1的顶点即为上述D中Inf的顶点)。
preform_dijkstra_path_extraction.m:提取dijkstra算法所得到的路径。
function path = perform_dijkstra_path_extraction(A,D,end_points)
参数说明:A——上述使用gen_square_graph方法生成的A矩阵。
D——上述perform_dijkstra得到的D向量,记录到起点的距离,大小为n^2*1.
end_points——终点。
输出:path——输出路径。为经过的顶点序列号。
plot_dijkstra.m:画出结果
function plot_dijkstra(A, vertex, S, path, start_points,end_points, options )
参数说明:同上述参数
输出:如下图
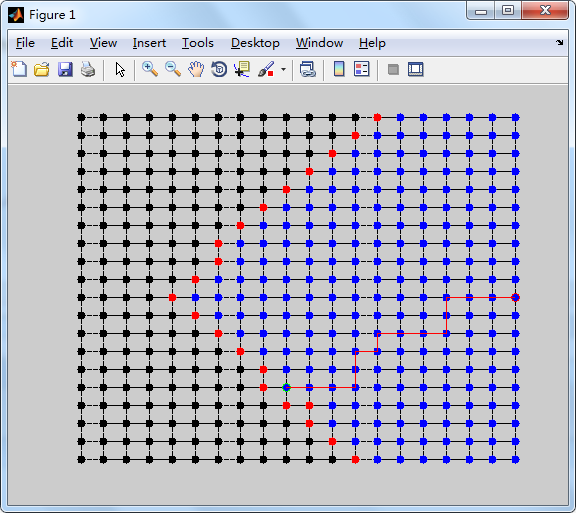
红线表示最短路径,蓝点表示dijkstra算法计算了距起点距离的点,红点为分界线,黑点为Inf。分别对应perform_dijkstra中的输出S的三种状态值。
一点思考:如果用在三维中求测地距离,那么就需要先将.off文件转化为graph,并求出顶点间的距离(也即权重),然后就可以用dijkstra算法求出没两个顶点之间的测地距离。相比于上面的求解,要解决的问题是怎样计算三维模型顶点间的距离:首先计算邻接矩阵A,当两顶点相连则为1;然后计算权重矩阵B,也即欧式距离矩阵;最后preform_dijkstra即可得到测地距离矩阵。下面是对正八面体进行试验的代码:
clear;
[vertex,face] = read_off('test.off');
A = triangulation2adjacency(face,vertex);
B = zeros(size(A,1),size(A,2));
for i = 1:size(A,1)
for j = 1:size(A,2)
if(A(i,j) == 1)
%B(i,j) = sqrt((vertex(1,i)-vertex(1,j))^2+(vertex(2,i)-vertex(2,j))^2+(vertex(3,i)-vertex(3,j))^2);
B(i,j) = sqrt((vertex(:,i)-vertex(:,j))'*(vertex(:,i)-vertex(:,j)));
end
end
end
[D,S] = perform_dijkstra(B, 2);