文献阅读报告

目录

概览

1. 描述：模型基于LSTM神经网络提出新型的Spatio-Temporal Graph（时空图），旨在实现在拥挤的环境下，通过将行人-行人，行人-静态物品两类交互纳入考虑，对行人的轨迹做出预测。

2. 训练与测试数据库

   1. 数据库：ETH Walking Pedestrian & UCY Students and Zara
   2. 数据：请参见https://www.cnblogs.com/sinoyou/p/11227348.html

   QUESTION

   数据库ETH和UCY中均只提供行人的轨迹坐标信息，未提供静态物体的坐标和分类方式，有关Obstacle的数据来源未知。

3. 评价指标与评价结果

   1. ADE（Average Displacement Error） - 计算出每位行人整个轨迹偏差的均值，再对所有行人取平均。

      ADE = $$Sigma^N_{j=1}{Sigma^n_{i=1}sqrt{(hat x_i^j - x_i^j)^2 + (hat y_i^j - y_i^j)^2} over n} over N$$

   2. FDE（Final Displacement Error）- 计算出每位行人轨迹重点的偏差，再对所有行人取平均。

      FDE = $$Sigma^N_{j=1}{sqrt{(hat x_n^j - x_n^j)^2 + (hat y_n^j - y_n^j)^2}} over N$$

   3. 评价结果：

      1. 对比其他Graph-based baselines：S-RNN、Social Attention等，H-H和H-H-O模型的平均测试结果能够减少最大为55%的ADE和61%的FDE。
      2. 对比Social LSTM和SGAN等其他模型，有以下重大提升：
         1. 在静止物体较多的数据集（如Hotel和UCY）中，H-H-O模型在FDE错误率上最高降低93%。
         2. 在人群密集处如入口（ETH）中，人群避免碰撞的情况常发生，H-H-O在FDE错误率上最高降低89%。
      3. 相比于其他模型，此模型更适合预测Finial Step，而不是Entire Step。

模型

本文在此将基于基于图的神经网络资料阅读整理的已有内容着重强调新模型运用Attention机制在原有SRNN模型基础上做出的改进，其他基础型内容请参见链接。

Spatio-Temporal Graph

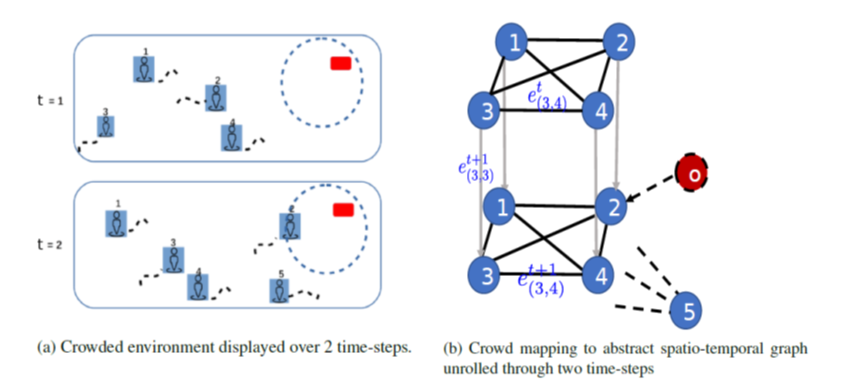
模型中的时空图有两类点和三类边

1. Pedestrian Node：行人点
2. Object Node：静态物品点
3. Spatial-Edge（两类）：同一时刻不同点之间的连边。所有行人之间都连有双向的Spatial-Edge，当行人很靠近Object时，有从Object指向行人的单向Spatial-Edge。
4. Temporal-Edge：相邻时刻连接相同行人点的单向边。

边权（edge features）定义

1. 不同点之间的边（Spatial-Edge）如(x_{v_1v_2})，表示两点之间距离。
2. 相同点之间的边（Temporal-Edge）如(x_{v_1v_1})，表示该点的位置。

LSTM替换st-graph中的部件

1. 将st-graph因式化分解，st-graph的点和边替换为LSTM序列后得到：temporal edgeLSTM, spatial edgeLSTM, nodeLSTM。
2. 同SRNN结构，nodeLSTM的输出时每一步预测的最终输出，在每一步运行时会将相邻edgeLSTMs的输出经过注意力机制后作为输入，层级在edgeLSTMs之上。

Edge LSTM

spatial edgeLSTM

​ 对于每条edge都有一个LSTM模型，为了适应后续nodeLSTM处理方式，对于spatial edges将统一处理同一个点为起点的所有spatial edges（以 · 表示）。

​ $$e^t_{v_2.} = phi(x_{v_2.}^t;W_s)$$ - embedding

​ $$h^t_{v_2.} = LSTM(h_{v_2.}^{t-1}, e^t_{v_2.}, W_s^{lstm})$$ - lstm cell

temporal edgeLSTM

​ 对于每个点都仅有一个temporal edgeLSTM，因此无需批量地处理。

​ $$e_{v_2v_2} = phi(x^t_{v_2v_2};W_t)$$ - embedding

​ $$h_{v_2v_2}^t = LSTM(h_{v_2v_2}^{t-1}, e_{v_2v_2}^t, W_t^{lstm})$$ - lstm cell

Node LSTM

QUESTION

Obstacle是否仅在建边时与pedestrian存在不同，而使用nodeLSTM等都与pedestrian一致？

假设nodeLSTM的输出满足二维正态分布

同SRNN模型，(v_2)的nodeLSTM将用注意力机制整合来自(v_2)相邻点之间edgeLSTM输出和(v_2)的temporal edgeLSTM输出作为输入的一部分（公式中(H_{v_2}^t)就是整合得到），最终基于LSTM的输出是二维正态分布的假设，求出预测的位置或计算损失值（与Social LSTM类似）。

[mu_{v_2}^{t+1}, sigma_{v_2}^{t+1}, ho_{v_2}^{t+1} = W_{out}h_{v_2}^t ]

[(x_{v_2}^{t+1}, y_{v_2}^{t+1}) sim N(mu_{v_2}^{t+1}, sigma_{v_2}^{t+1}, ho_{v_2}^{t+1}) ]

根据文章的解释，(x^t_{v_2})和(x^t_{v_2v_2})应该相等，即temporal edgeLSTM和nodeLSTM从st-graph所获取的features应该是一样的。

Node LSTM

[e_{v_2}^t = phi(x_{v_2}^t; W_{embed}) $$ - embedding $$h_{v_2}^t = LSTM(e_{v_2}^t, concat(h_{v_2}^t, H_{v_2}^t, e_{v2}^t), W^{lstm})$$ - lstm cell <br> #### $H_{v_2}^t$的运算 文献中对于$H_{v_2}$的计算方式已经通过图示展现的很清晰明显了，大体就是将来自spatial edgeLSTM和temporal edgeLSTM的输出$h_{v_2.}^t,h_{v_2v_2}^t$经过PRelu和softmax得到的归一化$hat e_{v_2.}$，与源数据作乘法得到注意力权重$a_{v_2}^t$，将这些权重累加并取平局即得到加权平均的隐藏状态$H_{v_2}$。 > QUESTION > > 该文献与其他文献对于注意力权重的称呼有所不同，其他参考文献中将经过softmax归一化的数据称作注意力权重（coefficient），即$hat e_{v_2}$，将$a_{v_2}.$称作加权结果，但该文献中将$a_{v_2}.$称作注意力权重，权重之和再平均就是加权的隐藏状态。  模型在求得$H_{v_2}$使用的正是注意力机制，在借鉴了multi-head attention机制后改进出multi-node attention机制，有以下几个要点： 1. 引入了PReLU函数，相比于常规Relu有一个可训练的参数P，以便让负值隐藏值有细微跨度差异，实验证明对效果有提升。 2. **multi-node vs multi-head**：相较于multi-head attention，模型提出的注意力模型没有使用scale dot-product操作，而是用累加和平均的方式，也就没有大幅压缩向量维度，保留信息更充分。]