General Matrix Multiplication

GEMM is "General Matrix Multiplication", that is we won't consider optimizing some special cases, e.g. sparse matrix.

In this blog, I will introduce some optimization methods of GEMM step by step, including these subjects:

• CPU Cache
  • Naive GEMM on CPU
  • Row-oriented (Cache-friendly)
  • Divide matrix in tiles (more cache-friendly)
  • Multiple threads
• GPU and CUDA programming
  • Naive GEMM using CUDA
  • Shared memory within each block
  • Memory mapping between host and device (to reduce the latency of memory-copy)

You can find all the source code in this repo.

GEMM on CPU

In this blog, we will compute multiplication of two matrices A = (m, n), B = (n, k), and store the result in C = (m, k).

To simplify the implementation details, we assume that all matrices are size of SIZE x SIZE ( SIZE = 1024 is defined in include/config.h).

So if you see m, n, k in the following code, they are equal to SIZE = 1024.

Matrix class

First, we should implement a class for Matrix.

struct Matrix
{
    int rows, cols;
    float *elements;
    Matrix(int m, int n) : rows(m), cols(n), elements((float *)aligned_alloc(32, sizeof(float) * m * n)) {}

    void Destroy() { free(elements); }

    size_t Size() const { return (size_t)rows * cols; }

    void Randomize()
    {
        for (int i = 0; i < rows * cols; ++i)
            elements[i] = (rand() / RAND_MAX);
    }

    void Fill(float val = 0) { std::fill(elements, elements + rows * cols, val); }

    inline float &Get(int i, int j) const { return elements[i * cols + j]; }
};

Naive method

void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    int m = A.rows, n = A.cols, k = C.cols;
    for (int i = 0; i < m; ++i)
    {
        for (int j = 0; j < k; ++j)
        {
            float res = 0;
            for (int idx = 0; idx < n; ++idx)
                res += A.Get(i, idx) * B.Get(idx, j);
            C.Get(i, j) = res;
        }
    }
}

This naive method is very slow, since it accesses matrix B in a column-oriented way. It's not cache-friendly code.

Row-oriented

void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    int m = A.rows, n = A.cols, k = C.cols;
    for (int i = 0; i < m; ++i)
        for (int idx = 0; idx < n; ++idx)
            for (int j = 0; j < k; ++j)
                C.Get(i, j) += A.Get(i, idx) * B.Get(idx, j);
}

Now, the three matrices are accessed in row-oriented way.

Let's compare the "naive" method and "row-oriented" method via a simple test.

Name                AvgTime(ms)         AvgCycles
cpu_naive           2811.493643         6477681304.000000   
cpu_opt_loop        205.974141          474561720.000000    

Divide Matrix in Tiles

static constexpr int TILE = 2;
static inline void ComputeTile(Matrix A, Matrix B, Matrix C, int x, int y)
{
    for (int i = x; i < x + TILE; ++i)
        for (int j = y; j < y + TILE; ++j)
            for (int idx = y; idx < y + TILE; ++idx)
                C.Get(i, j) += A.Get(i, idx) * B.Get(idx, j);
}

void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    for (int i = 0; i < C.rows; i += TILE)
        for (int j = 0; j < C.cols; j += TILE)
            ComputeTile(A, B, C, i, j);
}

The value of TILE depends on the size of cache. You can change TILE and test on your machine.

Why I set TILE = 2?

• On my machine, the size of cache-line is 64 bytes (16 float).
• In each tile, we need to access total three tiles (tile of A, B, C).
• That is, one tile of each matrix has 2 * 2 = 4 float elements, totally 12 float.
• If we set TILE = 4, then totally 4 * 4 * 3 = 48 float, beyond one cache line.

Multiple Threads

There are 4 cores on my machine, so I divide matrix C into 4 parts. Each thread compute one part of C.

static constexpr int TILE = 2;
static constexpr int THREADS = 4; // There are 4 cores on my machine.

static inline void ComputeTile(Matrix A, Matrix B, Matrix C, int x, int y)
{
    for (int i = x; i < x + TILE; ++i)
    {
        for (int j = y; j < y + TILE; ++j)
        {
            float res = 0;
            for (int idx = y; idx < y + TILE; ++idx)
                res += A.Get(i, idx) * B.Get(idx, j);
            C.Get(i, j) += res;
        }
    }
}

void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    std::vector<std::thread> pool;
    auto task = [&](int x0, int y0, int x1, int y1)
    {
        for (int i = x0; i < x1; i += TILE)
            for (int j = y0; j < y1; j += TILE)
                ComputeTile(A, B, C, i, j);
    };
    int m = C.rows, k = C.cols;
    pool.emplace_back(std::thread(task, 0, m / 2, 0, k / 2));
    pool.emplace_back(std::thread(task, 0, m / 2, k / 2, k));
    pool.emplace_back(std::thread(task, m / 2, 0, 0, k / 2));
    pool.emplace_back(std::thread(task, m / 2, 0, k / 2, 0));

    for (auto &t : pool)
        t.join();
}

SPMD with ISPC

ISPC is "Intel SPMD Compiler". For more details of ISPC, refer to IPSC User Guide.

But it seems that I wrote ISPC code in a naive way :-D, its performance is just-so-so. Maybe I should use foreach, task in ISPC to optimize it.

#define Get(array, i, j, cols) (array[i * cols + j])
#define TILE (2)
static inline void ComputeTile(
    uniform int m, uniform int n, uniform int k, 
    uniform float A[], 
    uniform float B[], 
    uniform float C[],
    uniform int tileRow, uniform int tileCol
)
{
    for (uniform int i = tileRow; i < tileRow + TILE; ++i)
    {
        for (uniform int j = tileCol; j < tileCol + TILE; ++j)
        {
            for (uniform int idx = tileCol; idx < tileCol + TILE; ++idx)
            {
                Get(C, i, j, k) += Get(A, i, idx, n) * Get(B, idx, j, k);
            }
        }
    }
}

export void MatrixMul(
    uniform int m, uniform int n, uniform int k, 
    uniform float A[], 
    uniform float B[], 
    uniform float C[]
)
{
    uniform int tileRow;
    uniform int tileCol;
    for (tileRow = 0; tileRow < m; tileRow += TILE)
    {
        for (tileCol = 0; tileCol < k; tileCol += TILE)
        {
            ComputeTile(m, n, k, A, B, C, tileRow, tileCol);
        }
    }
}

SIMD with AVX

Intel has "invented" some magic instructions, such as MMX, SSE, AXV.

For more details, you should read Intel Intrinsics Guide.

#include <immintrin.h>
#include <x86intrin.h>
#include "matrix.h"

constexpr int TILE = 8;
static inline void ComputeTile(Matrix A, Matrix B, Matrix C, int x, int y)
{
    int m = A.rows, n = A.cols, k = C.cols;

    /* store the result of C[i, j] */
    alignas(32) static float cval;

    /* store a colume of B in a tile */
    alignas(32) static float bvals[TILE];
    
    /* AVX variables */
    __m256 a, b, c;
    for (int i = x; i < x + TILE; ++i)
    {
        for (int j = y; j < y + TILE; ++j)
        {
            for (int idx = 0; idx < TILE; ++idx)
                bvals[idx] = B.Get(y + idx, j);

            a = _mm256_load_ps(&A.Get(i, y));
            b = _mm256_load_ps(bvals);
            c = _mm256_mul_ps(a, b);
            _mm256_store_ps(&cval, c);
            C.Get(i, j) = cval;
        }
    }
}

void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    /* We use TILE * sizeof(float) bit AVX here. */
    assert(TILE == 8);
    for (int i = 0; i < C.rows; i += TILE)
        for (int j = 0; j < C.cols; j += TILE)
            ComputeTile(A, B, C, i, j);
}

Tests

Let's put them together.

SIZE = 1024
Name                AvgTime(ms)         AvgCycles
cpu_naive           2547.440247         5869340770.000000   
cpu_opt_loop        191.350930          440873452.000000    
cpu_tile            2.353521            5421522.000000      
cpu_multi_threads   0.881988            2030816.000000      
spmd                5.795940            13352020.000000     
simd_avx            4.246814            9783934.000000  

However, the simple numbers DO NOT represent one method is good or bad (but cpu_naive and cpu_opt_loop is very bad, absolutely). The arguments of hardware on the machine will effect the performance of these methods, such as cache-size.

For example, in the above data, simd_avx is slower than cpu_tile.

• In cpu_tile, TILE = 2, the tiles of A, B, C is cache-friendly. They can put into one cache-line.
• In simd_avx, we set TILE = 8 since we want to use AVX256. So each tile of one matrix has 64 floats, they can not put into one cache-line. This is why simd_avx slower.
• But on others machines with larger L1-cache/L2-cache, simd_avx may faster, I think.

Anyway, it shows that these techniques (cache-friendly, SIMD, SPMD, AVX) do have an positive effect on GEMM.

GEMM on GPU

• In CUDA programming, we need to copy the host-memory to device-memory, I think the latency of memory-copy should be included in time of GEMM.
• In modern GPUs the shared memory size is only 64KB, while the register file size is 256KB. We should remember this when writing CUDA code.
• Before you read this section, you should have an overview of GPU and CUDA, refer to this blog.

Matrix class

I have made a special adaptation on Matrix class for using CUDA, see include/cuda_matrix.h in the source code.

Naive method

I "borrow" this figure from Nvidia CUDA Guide.

#include "cuda_matrix.h"

__global__ void DeviceMatrixMul(Matrix a, Matrix b, Matrix c)
{
    int row = blockIdx.x * blockDim.x + threadIdx.x;
    int col = blockIdx.y * blockDim.y + threadIdx.y;
    if (row < c.rows && col < c.cols)
    {
        float res = 0;
        for (int j = 0; j < a.cols; ++j)
            res += a.Get(row, j) * b.Get(j, col);
        c.Get(row, col) = res;
    }
}

__host__ void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    /* check validity of input matrice */
    assert(A.cols == B.rows && C.rows == A.rows && C.cols == B.cols);

    /* matrice in device memory */
    Matrix da(A.rows, A.cols, Memory::Device);
    Matrix db(B.rows, B.cols, Memory::Device);
    Matrix dc(C.rows, C.cols, Memory::Device);

    cudaMemcpy(da.elements, A.elements, sizeof(float) * A.Size(), cudaMemcpyHostToDevice);
    cudaMemcpy(db.elements, B.elements, sizeof(float) * B.Size(), cudaMemcpyHostToDevice);

    /* One thread compute one element C[i, j].
     * Max number of threads per block is 1024.
     */
    dim3 blockDim(CUDA_BLOCK_SIZE, CUDA_BLOCK_SIZE);
    dim3 gridDim(C.rows / blockDim.x + (C.rows % blockDim.x != 0),
                 C.cols / blockDim.y + (C.cols % blockDim.y != 0));
    DeviceMatrixMul<<<gridDim, blockDim>>>(da, db, dc);

    /* wait for device to finish its job */
    cudaDeviceSynchronize();
    cudaMemcpy(C.elements, dc.elements, sizeof(float) * C.Size(), cudaMemcpyDeviceToHost);
    da.Destroy(), db.Destroy(), dc.Destroy();
}

Shared Memory

• In naive method, we need to access elements from global memory (which is very "far" from SMs of GPU).
• Within each block, there is 64KB shared memory, we can leverage it.

#include "cuda_matrix.h"
__global__ void DeviceMatrixMul(Matrix A, Matrix B, Matrix C)
{
    int tx = threadIdx.x, ty = threadIdx.y;
    int row = blockIdx.x * CUDA_BLOCK_SIZE + tx;
    int col = blockIdx.y * CUDA_BLOCK_SIZE + ty;

    /* result of C[i, j] */
    float res = 0;

    /* shared memory within block */
    __shared__ float sharedA[CUDA_BLOCK_SIZE][CUDA_BLOCK_SIZE];
    __shared__ float sharedB[CUDA_BLOCK_SIZE][CUDA_BLOCK_SIZE];

    for (int k = 0; k < A.cols; k += CUDA_BLOCK_SIZE)
    {

        sharedA[tx][ty] = (row < A.rows && k + ty < A.cols) ? A.Get(row, k + ty) : 0;
        sharedB[tx][ty] = (k + tx < B.rows && col < B.cols) ? B.Get(k + tx, col) : 0;
        __syncthreads();

        for (int j = 0; j < CUDA_BLOCK_SIZE; ++j)
            res += sharedA[tx][j] * sharedB[j][ty];
        __syncthreads();
    }
    if (row < C.rows && col < C.cols)
        C.Get(row, col) = res;
}

The MatrixMul is same with naive method, omit it here.

Memory Mapping

• In above code, we need to copy host-memory to device-memory. We can use "Memory Mapping" to reduce it.
• However, it seems that for very large matrix, mmap is slower than naive method. That's because each time SM need to access very "far" memory in host, while naive method only accesses them in relatively close device-memory.

/* Matrix Multiplication on CUDA, based on block shared memory and memory mapping. */
#include "cuda_matrix.h"
__global__ void DeviceMatrixMul(Matrix A, Matrix B, Matrix C)
{
    int tx = threadIdx.x, ty = threadIdx.y;
    int row = blockIdx.x * CUDA_BLOCK_SIZE + tx;
    int col = blockIdx.y * CUDA_BLOCK_SIZE + ty;

    /* result of C[i, j] */
    float res = 0;

    /* shared memory within block */
    __shared__ float sharedA[CUDA_BLOCK_SIZE][CUDA_BLOCK_SIZE];
    __shared__ float sharedB[CUDA_BLOCK_SIZE][CUDA_BLOCK_SIZE];

    for (int k = 0; k < A.cols; k += CUDA_BLOCK_SIZE)
    {

        sharedA[tx][ty] = (row < A.rows && k + ty < A.cols) ? A.Get(row, k + ty) : 0;
        sharedB[tx][ty] = (k + tx < B.rows && col < B.cols) ? B.Get(k + tx, col) : 0;
        __syncthreads();

        for (int j = 0; j < CUDA_BLOCK_SIZE; ++j)
            res += sharedA[tx][j] * sharedB[j][ty];
        __syncthreads();
    }
    if (row < C.rows && col < C.cols)
        C.Get(row, col) = res;
}
void MatrixMul(Matrix A, Matrix B, Matrix C)
{
    int m = A.rows, n = A.cols, k = C.cols;
    /* allocate mapping memory */
    Matrix da(m, n, Memory::EMPTY);
    Matrix db(n, k, Memory::EMPTY);
    Matrix dc(m, k, Memory::EMPTY);

    dim3 blockDim(CUDA_BLOCK_SIZE, CUDA_BLOCK_SIZE);
    dim3 gridDim(m / blockDim.x + (m % blockDim.x != 0),
                 k / blockDim.y + (k % blockDim.y != 0));

    /* create matrice accessed by device */
    assert(cudaHostGetDevicePointer(&da.elements, A.elements, 0) == cudaSuccess);
    assert(cudaHostGetDevicePointer(&db.elements, B.elements, 0) == cudaSuccess);
    assert(cudaHostGetDevicePointer(&dc.elements, C.elements, 0) == cudaSuccess);

    DeviceMatrixMul<<<gridDim, blockDim>>>(da, db, dc);

    /* let host wait for device to finish its job */
    cudaDeviceSynchronize();
}

Tests

The result "mmap" seems special, we will explain this result in "Evaluation" section.

• When size of matrices is very very small, e.g. SIZE <= 128, mmap method is faster than naive method and shm method, since it reduces the latency of memory copy.
• When size getting larger, e.g. SIZE >= 128, mmap method become very slow, even slower than naive method. And in such case, shm is the best among these three method.

SIZE = 16
Name                AvgTime(ms)         AvgCycles
cuda_mat_mul        68.517565           157858096.000000    
cuda_mat_mul_shm    35.874186           82649984.000000     
cuda_mat_mul_mmap   0.390858            900192.000000   

SIZE = 1024
Name                AvgTime(ms)         AvgCycles   
cuda_mat_mul        285.567492          657942456.000000    
cuda_mat_mul_shm    131.548488          303084320.000000    
cuda_mat_mul_mmap   484.942781          1117301924.000000       

Evaluation

The original data of test result is here.

GEMM on CPU

Let's have a look on the performance of GEMM on CPU. I compare some improved methods with naive method. The y-axis of figure 1-3 show their times of speedup, compared with naive method, i.e. \(T_{\text{naive}} / T_{\text{method}}\).

• cpu_opt_loop: Change the order of for-loop, it access three matrices in a row-oriented way.
• cpu_tile: Divide matrix into some tiles, and conquer each of them.
• cpu_multi_threads: Divide result matrix C into 4 parts, create 4 threads (there are 4 core on my machine) to compute each part of C using the method of cpu_tile.
• spmd_ispc: Based on the method of cpu_tile, the Intel-ISPC library is used to improve the parallelism of the program. (I wrote ISPC code in a just-so-so way, so the performance seems not pretty good.)
• simd_avx: Base on the method of cpu_tile, AVX instructions is used to compute 8 float-multiplications in one instructions cycle.
  • Actullay, using the flags -funroll-all-loops and -O3 of gcc/g++, the complier will help us generate vectorize instructions.
  • Or use marco #prama unroll before some specific for-loops.

Result analysis:

• For SIZE = 16, ..., 128, best method is cpu_tile.
• For SIZE >= 256, cpu_multi_threads is the best, since L1-cache of each core is fully utilized in this method.

Conclusion:

• The main performance bottleneck of GEMM is memory accessing (I/O), more specifically, is the bandwidth of DRAM.
• Writing cache-friendly code will powerfully speedup our algorithm.
• Vectorization is good to help, but it relies heavily on hardware implementation.

Figure - 1	Figure - 2	Figure - 3

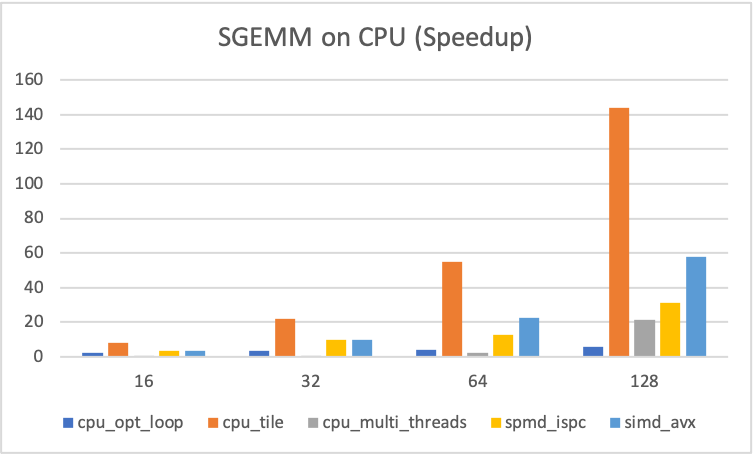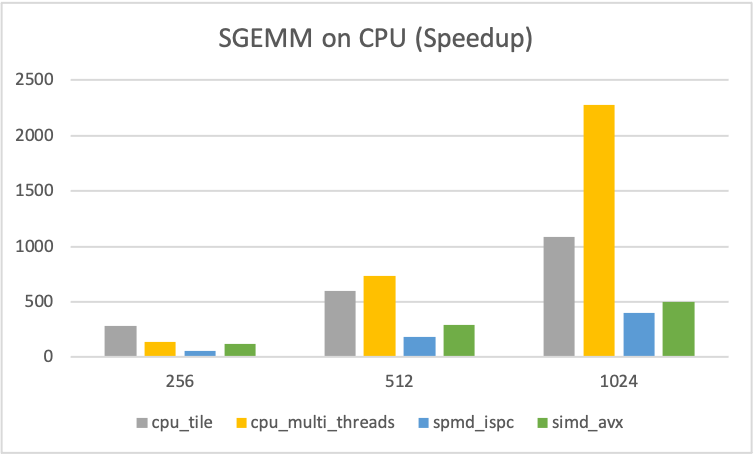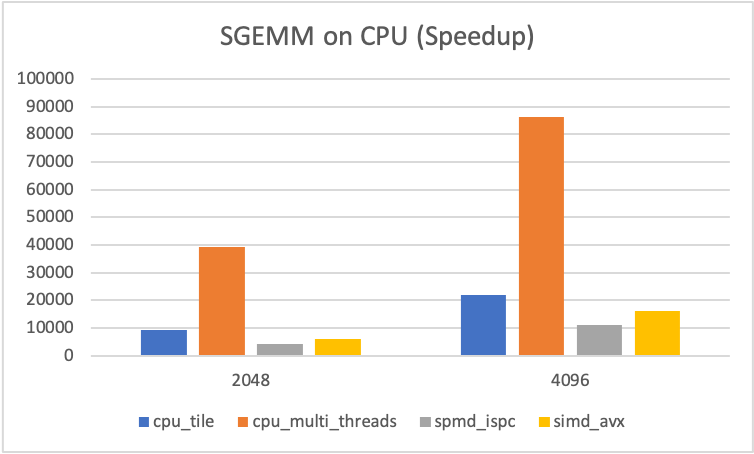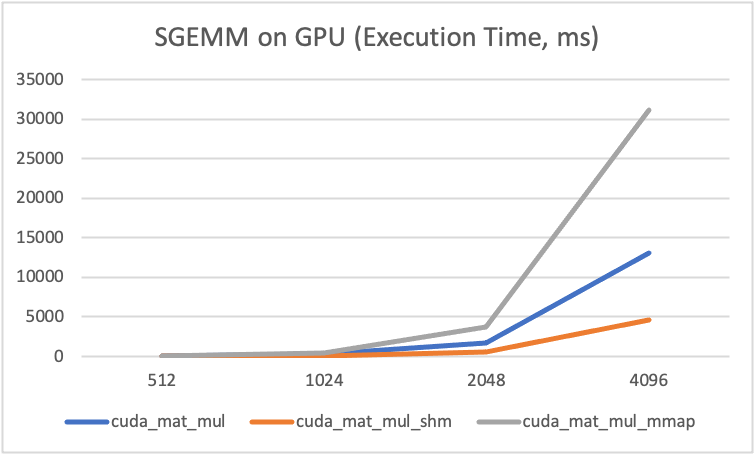
GEMM on GPU

I write three methods of GEMM using CUDA.

• cuda_mat_mul: Naive method, one thread compute one C[i, j].
• cuda_mat_shm: Utilized shared memory within each block, to reduce the latency of memory-accessing.
• cuda_mat_mmap: Memory mapping between host and device, to reduce latency of memory-copy.

Analysis:

• The y-axis represents computation time.
• When size is smaller, mmap is great, since it reduces memory-copy and it takes very little time to compute C[i, j] in such case. And when first time to access A[i, j], B[i, j], C[i, j], they can be cached in registers and cache of GPU.
• When size getting larger, mmap become worse than naive method, shm becomes the best among these three.
• It shows the conclusion again, the bottleneck of GEMM is memory accessing (I/O) and bandwidth of DRAM.

Figure - 4	Figure - 5

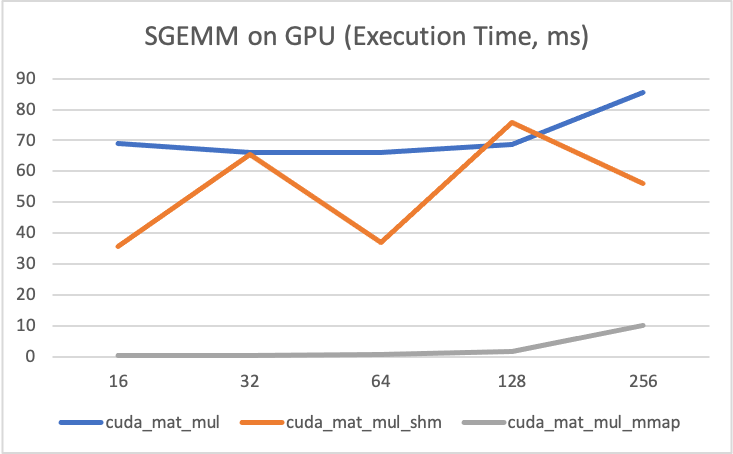CPU v.s. GPU

Is GPU better than CPU? According to test results on my machine (Intel i5 v.s. Nvidia 960M), that's not true.

Actually, for small size of GEMM, simple multi-threads on CPU is better than GPU. Because we always need to copy data from host to device in CUDA programming, the latency of this is "heavy". GPU is suitable for large-scale matrix operations, I think.

Strassen Algorithm

The algorithms above are \(O(n^3)\), but we have \(O(n^{2.7})\) algorithm - Strassen algorithm.

Its main idea is using addition and substraction to reduce one multiplication. (The cycle of mul is longer than add, sub.)

And we have:

The Strassen algorithm defines instead new matrices:

Now we can using 7 multiplications instead of 8 to compute matrix C.

But the cost here is, we need to frequently allocate and free buffer of M[i], it brings some cons.