关键词:位姿估计 OpenCV::solvePnP
用途:各种位姿估计
文章类型:原理、流程、Demo示例
@Author:VShawn(singlex@foxmail.com)
@Date:2016-11-18
@Lab: CvLab202@CSU
目录
前言
本文通过迭代法解PNP问题,得到相机坐标系关于世界坐标系的旋转矩阵R与平移矩阵T后,根据之前的文章《根据相机旋转矩阵求解三个轴的旋转角》获得相机坐标系的三轴旋转角,实现了对相机位姿的估计。知道相机在哪后,我们就可以通过两张照片,计算出照片中某个点的高度,实现对环境的测量。
先看演示视频:
原理简介
相机位姿估计就是通过几个已知坐标的特征点,以及他们在相机照片中的成像,求解出相机位于坐标系内的坐标与旋转角度,其核心问题就在于对PNP问题的求解,这部分本文不再啰嗦,参见本人之前的博客文章《相机位姿估计0:基本原理之如何解PNP问题》。本文中对pnp问题的求解直接调用了OpenCV的库函数"solvePnP",其函数原型为:
bool solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=ITERATIVE )
第一个输入objectPoints为特征点的世界坐标,坐标值需为float型,不能为double型,可以输入mat类型,也可以直接输入vector<point3f> 。
第二个输入imagePoints为特征点在图像中的坐标,需要与前面的输入一一对应。同样可以输入mat类型,也可以直接输入vector<point3f> 。
第三个输入cameraMatrix为相机内参数矩阵,大小为3×3,形式为:
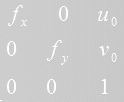
第四个输入distCoeffs输入为相机的畸变参数,为1×5的矩阵。
第五个rvec为输出矩阵,输出解得的旋转向量。
第六个tvec为输出平移向量。
第七个设置为true后似乎会对输出进行优化。
最后的输入参数有三个可选项:
CV_ITERATIVE,默认值,它通过迭代求出重投影误差最小的解作为问题的最优解。
CV_P3P则是使用非常经典的Gao的P3P问题求解算法。
CV_EPNP使用文章《EPnP: Efficient Perspective-n-Point Camera Pose Estimation》中的方法求解。
流程
1.从函数的原型看出函数需要相机的内参数与畸变参数,于是相机标定是必不可少的,通过OpenCV自带例程或者Matlab的相机标定工具箱都可以很方便地求出相机标定参数。
2.准备好四个特征点的世界坐标,存入Mat矩阵
vector<cv::Point3f> Points3D;
Points3D.push_back(cv::Point3f(0, 0, 0)); //P1 三维坐标的单位是毫米
Points3D.push_back(cv::Point3f(0, 200, 0)); //P2
Points3D.push_back(cv::Point3f(150, 0, 0)); //P3
Points3D.push_back(cv::Point3f(150, 200, 0)); //P4
3.准备好四个特征点在图像上的对应点坐标,这个坐标在实验中我是通过PhotoShop数出来的。注意,输入坐标的顺序一定要与之前输入世界坐标的顺序一致,就是说点与点要对应上,OpenCV的函数无法解决点与点匹配的问题(对应搜索问题)。
vector<cv::Point2f> Points2D;
Points2D.push_back(cv::Point2f(3062, 3073)); //P1 单位是像素
Points2D.push_back(cv::Point2f(3809, 3089)); //P2
Points2D.push_back(cv::Point2f(3035, 3208)); //P3
Points2D.push_back(cv::Point2f(3838, 3217)); //P4
4.创建输出变量,即旋转矩阵跟平移矩阵的变量。最后调用函数。
//初始化输出矩阵
cv::Mat rvec = cv::Mat::zeros(3, 1, CV_64FC1);
cv::Mat tvec = cv::Mat::zeros(3, 1, CV_64FC1);
//三种方法求解
solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_ITERATIVE); //实测迭代法似乎只能用共面特征点求位置
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_P3P); //Gao的方法可以使用任意四个特征点
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_EPNP);
5将输出的旋转向量转变为旋转矩阵
//旋转向量变旋转矩阵
double rm[9];
cv::Mat rotM(3, 3, CV_64FC1, rm);
Rodrigues(rvec, rotM);
6.最后根据《根据相机旋转矩阵求解三个轴的旋转角》一文求出相机的三个旋转角,根据《子坐标系C在父坐标系W中的旋转》求出相机在世界坐标系中的位置。
至此,我们就求出了相机的位姿。
实验
本人在实验中先后使用了两台相机做测试,一台是畸变较小的sony a6000微单+35mm定焦镜头,另一台是畸变较重的130w的工业相机+6mm定焦广角镜头,实验中两台相机都得到了正确的位姿结果,此处为了方便只用α6000微单做演示说明。

如上图所示,四个特征点P1-P4的世界坐标与像素坐标都已在图中标明,P5用于重投影验证位姿解是否正确。
相机实际位姿大约为:



粗略读出卷尺读数,得到相机的世界坐标大约为(520,0,330)。细心的读者应该发现了,上面几张图的特征点不一样了,其实是我中途重新做了一张特征点图,重新安放实验装置的时候已经尽量按照(520,0,330)这个坐标去安放了,但误差肯定是不可避免的。
把参数输入例程中,得到结果,计算出相机的世界坐标:

也就是(528.6,-2.89,358.6),跟实际情况还是差不多的。
同时还得到了x y z轴的三个旋转角

自己动手转一转相机,发现也是对的。
对P5点重投影,投影公式为:
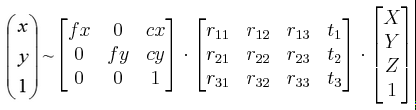
结果为:

误差在10pix以内,结果也是正确的,于是验证完毕。
P.S.经本人测试发现,solvePnP提供的三种算法都能对相机位姿进行估计,虽然三者直接解出的结果略有不同,但都在误差范围之内。其中solvePnP的默认方法迭代法,似乎只能使用共面的四个特征点求位姿,一旦有一个点不共面,解出的结果就会不对。
例程
最后给出例程,例程基于VS2013开发,使用的是OpenCV2.4.X,大家运行前需要将opencv的路径重新配置成自己电脑上的,不懂的话参考我的博客《OpenCV2+入门系列(一):OpenCV2.4.9的安装与测试》。例程中提供两张照片,其中DSC03323就是"实验"中所用图片,例程在计算完成后,会在D盘根目录下生成两个txt,分别存储:相机在世界坐标系的坐标、相机的三个旋转角。
下载地址:
CSDN:http://download.csdn.net/detail/wx2650/9688155
GIT:https://github.com/vshawn/Shawn_pose_estimation_by_opencv
最后
我现在在外地出差,演示视频里的东西就下一篇文章中再说了,敬请期待。