标题:螺旋折线
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【样例输入】
0 1
【样例输出】
3
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
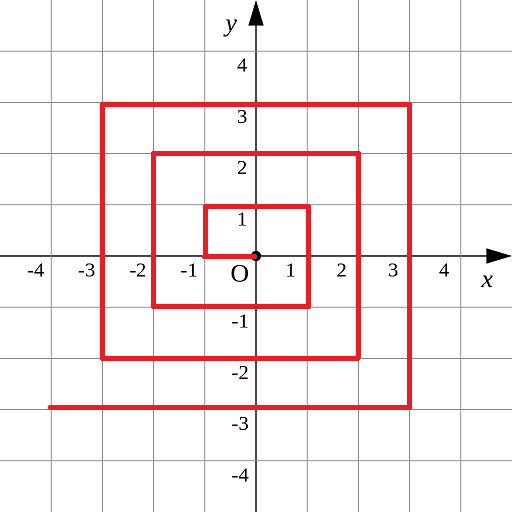
思路:我们将(0.0)点向下折一次,构成一个正方形;在将(-1,-1)点向下折一次,构成一个正方形;一次类推,折y=x轴上的点向下,得到多个正方形。每个正方形的边长差为8,此时我们可以使用等差数列求解。
解法:
#include<iostream> #include<math.h> using namespace std; int max(int x,int y) { return abs(x) > abs(y) ? abs(x) : abs(y); } int main() { int all_count= 0; int d; int every_count = 0; int x, y; cin >> x >> y; d = max(x, y); //由图中,我们可以将螺旋曲线看成是一个个正方形,他们的边长差为8 if(x>=y) { //当x>y时,我们求出前d层(包括d层)边的个数,算出(x,y)距(-d,-d)的距离,然后相减 every_count = x - (-d) + y - (-d); all_count = 8 * d + d*(d - 1) / 2 * 8 - every_count; cout << all_count << endl; } else if(x<y) { //当x<y时,我们求出前d-1层(包括d-1层)边的个数,算出(x,y)距(-d,-d)的距离,然后相加 every_count = x - (-d) + y - (-d); all_count = 8 * (d-1) + (d-2)*(d - 1) / 2 * 8 +every_count; cout << all_count << endl; } return 0; }
此时时间复杂图为O(1)。