算法探险之链表

算法探险之链表
https://mdnice.com/writing/dfe9b67d49e94294ab516d9438716593

JS算法探险之链表
❝
子曰：“吾十有五而志于学，三十而立，四十而不惑，五十而知天命，六十而耳顺，七十而「从心所欲不逾矩」 --「《论语·第二章·为政篇》」
❞

大家好，我是「柒八九」。一个立志要成为「海贼王的男人」。

说起，「链表」在前端领域，可能有些许的陌生。但是，它作为一个传统的数据结构，在一些高价领域还是有用武之地的。

例如，了解React的朋友，都听说过React-16+对调和算法Reconciliation Algorithm进行了重构，一个React应用不仅有和DOM树一一对应的Vritual-DOM（现在一般说React-Element）,还存在一种叫Fiber的结构。而该结构用于实现一些比较高级的特性。

而Fiber就是用链表实现的。
Fiber-TreeEffect-List
针对React的新架构，我们会有一篇文章来介绍。

而今天，我们讲一讲，JS中针对「链表」类型的相关算法的解题技巧和一些注意事项。

这里是算法系列的往期文章。

文章list
天不早了，我们干点正事哇。

--

链表-打油诗
- 链表算法多又杂，既定工具来报道
- 简化「创建」/「删除」头节点，dumy节点来相助
- 「双指针」又来到，解决问题不能少
  
  「前后双指针」-> 倒数第k个节点
  
  「快慢双指针」 -> 找「中点」/判断环/找环入口
- 反转链表，三板斧，prev/cur/next
  
  「先存后续」(next= cur.next)
  
  在修改引用(cur.next = prev)
  
  暂存当前节点(prev= cur)
  
  后移指针(cur=next)
- 常用工具要记牢，遇到问题化繁为简，拼就完事
文章概要
1. 哨兵节点
2. 双指针
3. 反转链表
知识点简讲

链表是个啥

计算机的内存就像「一大堆格子」，每格都可以用来保存「比特形式」的数据。

当要创建「数组」时，程序会在内存中找出「一组连续的空格子」，给它们起个名字，以便你的应用存放数据。

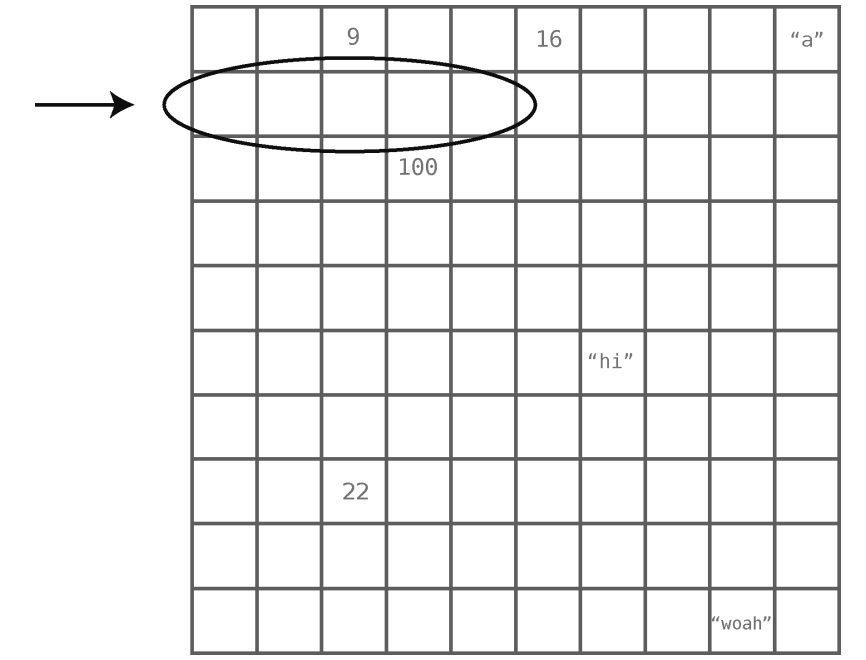
与数组不同的是，组成「链表的格子不是连续的」。它们可以分布在内存的各个地方。这种不相邻的格子，就叫作「结点」。

链表的每个元素都存储了下一个元素的地址，从而使「一系列随机的」内存地址串在一起。

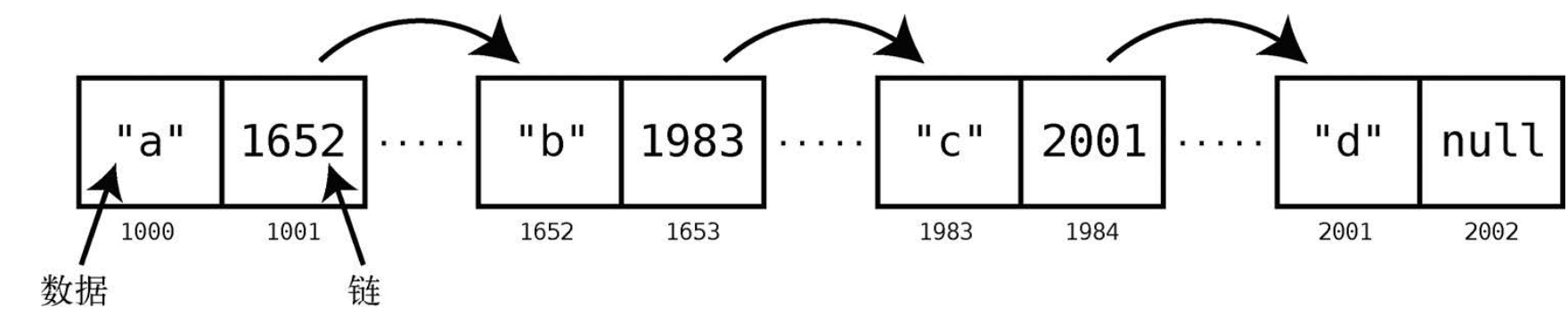
此例中，链表包含 4 项数据：a、b、c和d。因为每个结点都需要 2 个格子。
- 头一格用作「数据存储」
- 后一格用作指向下一结点的「链」（最后一个结点的链是 null，因为它是终点）
所以整体占用了 8 (4 x 2)个格子。

❝
链表相对于数组的一个好处就是，它可以「将数据分散到内存各处」，无须事先寻找连续的空格子
❞

构造链表节点

单向链表的节点代码
```
class ListNode {
      val: number
      next: ListNode | null
      constructor(val?: number, next?: ListNode | null) {
          this.val = (val===undefined ? 0 : val)
          this.next = (next===undefined ? null : next)
      }
  }
```
链表基础算法

其实，针对链表存在一些常规的「工具方法」。一些比较复杂的算法，都是各种工具方法的组合。

而下面的这些方法，是需要「熟记」的。

1. 链表反转

关键点解释：
- 需要「三个指针」
  
  各自初始值如下：
  
  perv = null
  
  cur = head
  
  next = cur.next
- 遍历的时候
  
  「先存后续」(next= cur.next)
  
  在修改引用(cur.next = prev)
  
  暂存当前节点(prev= cur)
  
  后移指针(cur=next)
```
function reverseList(head){
  // 初始化prev/cur指针
  let prev = null;
  let cur = head;
  // 开始遍历链表
  while(cur!=null){
    // 暂存后继节点
    let next = cur.next;
    // 修改引用指向
    cur.next = prev;
    // 暂存当前节点
    prev = cur;
    // 移动指针
    cur = next;
  }
  return prev;
};
```
2. 判断链表是否有环

关键点解释：
- 「快慢指针」
- 遍历的条件
  
  while(fast && fast.next)
```
function hasCycle(head){
  let fast = head;
  let slow = head;
  
  while(fast && fast.next){
    fast = fast.next.next;
    slow = slow.next;
    if(fast == slow) return true;
  }
  return false;
}
```
3. 合并链表

关键点解释：
- 为了规避，边界情况(l1/l2可能初始为空)，采用dumy节点
  
  dumy = new ListNode(0)
  
  定义一个零时指针node = dumy
- 处理l1/l2相同位置的节点信息
  
  while(l1 && l2)
  
  根据特定的规则，对链表进行合并处理
  
  node.next = lx (x=1/2)
  
  移动处理后的链表 lx = lx.next
- 处理l1/l2「溢出」部分的节点信息
  
  if(lx) node.next = lx;
- 返回整合后的首节点
  
  dumy.next
```
function mergeList(l1,l2){
  let dumy = new ListNode(0);
  let node = dumy;
  while(l1 && l2){
    node.next = l1;
    l1 = l1.next;
    
    node.next = l2;
    l2 = l2.next;
  }
  // 由于l1/l2长度一致
  if(l1) node.next = l1;
  if(l2) node.next = l2;
  return dumy.next;
}
```
4. 找中点

关键点解释：
- 利用「快慢指针」
  
  初始值
  
  slow = head
  
  fast = head
- 循环条件为
  
  fast && fast.next非空
- 指针移动距离
  
  fast每次移动两步 fast = fast.next.next
  
  slow每次移动一步 slow = slow.next
- 「处理链表节点为偶数的情况」
  
  跳出循环后，也就是fast.next ==null,但是，fast可能不为空
  
  如果fast不为空，slow还需要移动一步 slow = slow.next
- 最后，slow所在的节点就是链表的中间节点
```
function middleNode(head){
        let slow = head;
        let fast = head;
        // 遍历链表节点
        while (fast && fast.next) {
            slow = slow.next;
            fast = fast.next.next;
        }
        // 处理链表节点为偶数的情况
        if(fast){
          slow = slow.next;
        }
        return slow;
    }
```
1. 哨兵节点

❝
「哨兵节点」是为了简化处理链表「边界条件」而引入的「附加链表节点」
❞

哨兵节点通常位于「链表的头部」，它的值没有任何意义。在一个有哨兵节点的链表中，「从第二个节点开始才真正的保存有意义的信息」。

简化链表插入操作

链表的一个基本操作是在链表的尾部添加一个节点。由于通常只有一个指向单向链表头节点的指针，因此需要「遍历」链表的节点直到到达链表尾部，在尾部添加一个节点。

「常规方式」，在链表尾部添加元素
```
function append(head,value){
  let newNode = new ListNode(value);
  // 原始链表为空
  if(head ==null) return newNode;
  
  let node = head;
  // 遍历链表，直到链表尾部
  while(node.next!=null){
      node = node.next;
  }
  
  // 在尾部添加一个节点
  node.next = newNode;
  return head;
}
```
「哨兵节点」，在链表尾部添加元素
```
function append(head,value) {
  // 哨兵节点 
  let dumy = new ListNode(0);
  dumy.next = head;
  
  // 遍历链表，直到链表尾部
  let node = dumy;
  while(node.next!=null){
    node = node.next;
  }

  node.next = new ListNode(value);
  return dumy.next;
}
```
首先，创建一个「哨兵节点」（该节点的「值」没有意义 -即ListNode(0)参数为啥不重要），并把该节点当做链表的头节点，「把原始的链表添加到哨兵节点的后面」（dumy.next = head）。

然后，返回真正的头节点（哨兵节点的下一个节点）node.next

这里有一个小的注意点，就是在「遍历」链表的时候，并不是直接对dumy进行处理，而是用了一个「零时游标节点」(node)。这样做的好处就是，在append操作完成以后，还可以通过dumy节点来，直接返回链表的头节点dumy.next。因为,dumy一直没参与遍历过程。

简化链表删除操作

如何从链表中删除第一个值为「指定值」的节点？

❝
为了删除一个节点，需要找到被删除节点的「前一个节点」，然后把该节点的next指针指向它「下一个节点的下一个节点」。
❞

「常规方式」，在删除指定节点
```
function delete(head,value) {
  if(head==null) return head
  // 处理头节点
  if(head.val==value) return head.next;
  
  // 遍历链表，直到满足条件
  let node = head;
  while(node.next!=null){
    if(node.next.val ==value){
      node.next = node.next.next;
      barek;
    }
    node = node.next;
  }
  return head;
}
```
在代码中，有两天if语句，分别是处理两个「特殊情况」：
- 输入的「链表为空」 head==null => return head
- 被删除的节点是原始链表的「头节点」 head.val == value =>return head.next
在遍历链表的时候，时刻判断「当前节点的下一个节点」node.next。

删除某个节点的操作node.next = node.next.next

「哨兵节点」，在删除指定节点
```
function delete(head ,value){
  let dumy = new ListNode(0);
  dumy.next = head;
  
  let node = dumy;
  while(node.next!=null){
    if(node.next.value==value){
      node.next = node.next.next;
      barek;
    }
    node = node.next;
  }
  return dumy.next;
}
```
通过哨兵节点(dumy)直接将「链表为空」和「被删除节点是头节点」的两种特殊情况，直接囊括了。用最少的代码，处理最多的情况。

❝
使用哨兵节点可以简化「创建」或「删除」链表头节点的操作代码
❞

2. 双指针

利用「双指针」解决问题，是一种既定的套路。
- 在JS算法之数组中我们通过「双指针」的技巧,处理数组数据为「正整数」的情况
  
  「数据有序」反向针，left为首right为尾(求两数之和)
  
  「子数组」同向针，区域之「和」或「乘积」
- 在JS算法之字符串中我们通过「双指针」的「反向双指针」技巧，处理「变位词」、「回文串」等问题
而针对「链表」的一些特定题目，也可以利用双指针的解题思路。

在链表中，双指针思路又可以根据两个指针的不同「移动方式」分为两种不同的方法。
❝

「前后双指针」：即一个指针在链表中「提前」朝着指向下一个节点的指针移动「若干步」，然后移动第二个指针。
「应用」：查找链表中倒数第k个节点

「快慢双指针」：即两个指针在链表中「移动的速度不一样」，通常是「快的指针」朝着指向下一个节点的指针「一次移动」两步，「慢的指针一次只移动一步」。
「特征」：在一个「没有环」的链表中，当快的指针到达链表尾节点的时候，慢的指针正好指向链表的「中间节点」

❞
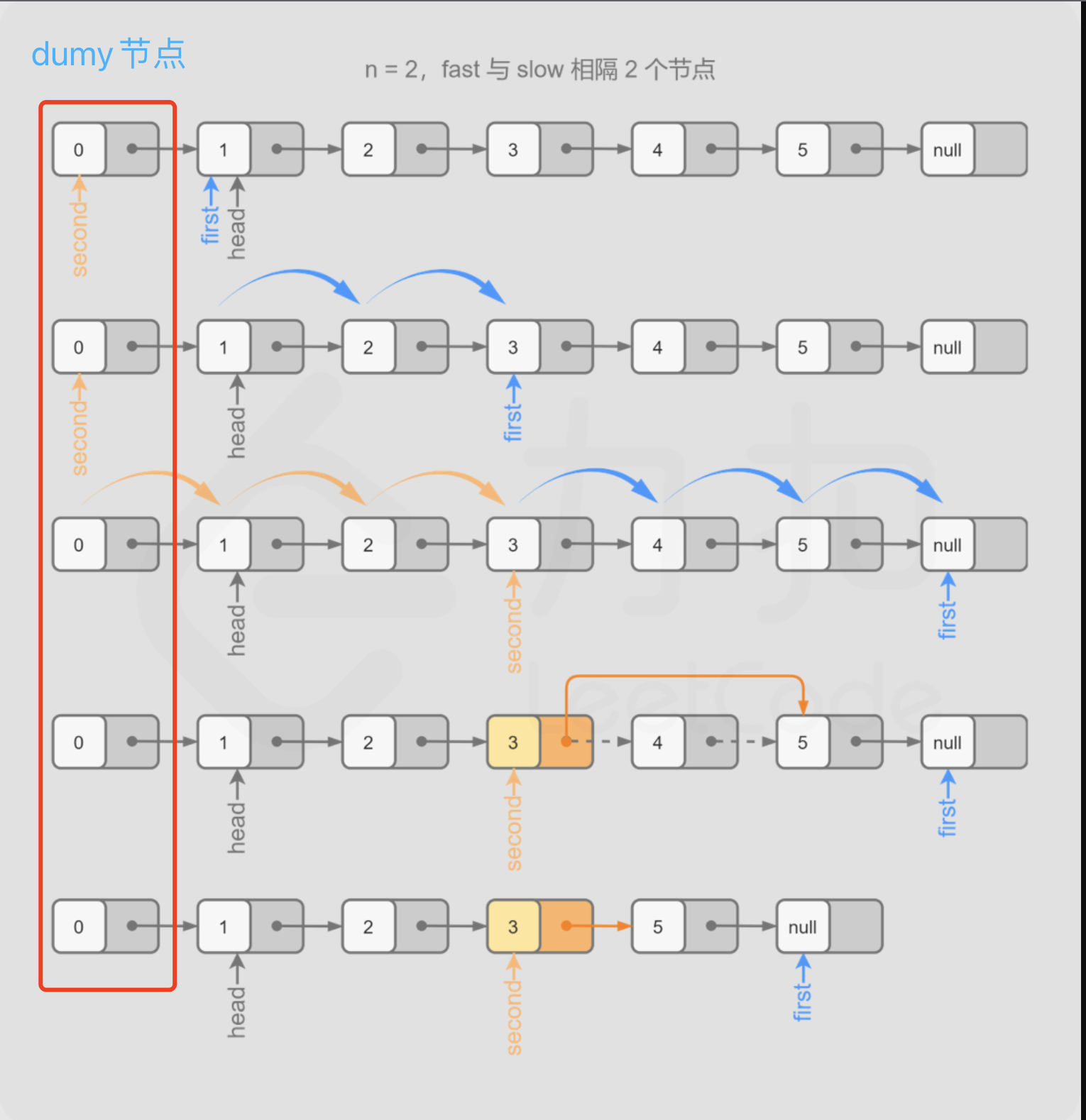
删除倒数第k个节点

题目描述：

❝
给定一个链表，删除链表中「倒数」第k个节点
提示：
假设链表中节点的总数为n且 1≤ k ≤ n
「只能遍历一次链表」

示例：链表为 1->2->3->4->5,删除倒数第2个节点后链表为1->2->3->5，删除了4所在的节点
❞

分析
1. 题目要求只能遍历一次链表，我们可以定义两个指针
  
  第1个指针 front从链表的头节点开始「向前走k步」的过程中，第2个指针back保持不动
  
  从第k+1步开始，back也从链表的头节点开始和front以相同的速度遍历
  
  由于「两个指针的距离始终保持为k」,当指针front指向链表的尾节点时（如果存在dumy节点的话，就是front指向尾节点的下一个节点），「指针back正好指向倒数第k+1个节点」
2. 我们要删除倒数第k个节点，而利用快慢双指针，我们可以找到倒数第k+1个节点,即「倒数k节点的前一个节点」，那更新倒数k+1节点的next指针，就可以将倒数k个节点删除
3. 当k等于链表的节点总数时，被删除的节点为原始链表的头节点，我们可以通过dumy节点来简化对此处的处理
4. 而由于dumy节点的出现，由于存在front/back两个指针，就需要对其进行初始化处理。
  
  p2：由于存在③的情况（删除原始链表头节点），所以back初始化「必须」是back=dumy（back指向dumy）
  
  p1：初始指向原始链表的头节点(front=head)
代码实现
```
function removeNthFromEnd(head,k){
  let dumy = new ListNode(0);
  dumy.next = head;
  
  let front = head; //指向原始链表头节点
  let back = dumy; // 指向dumy节点
  
  // front 向前移动了k个节点
  for(let i =0; i<k; i++){
    front = front.next;
  }
  // 同步移动
  while(front!=null){
    front = front.next;
    back = back.next;
  }
  // 删除第k个节点
  back.next = back.next.next;
  return dumy.next;
}
```
这里有一点再强调一下：

在同步移动的过程中，「只有」front移动到尾节点的下一个节点，即：null时，此时back节点才到了倒数k+1的位置

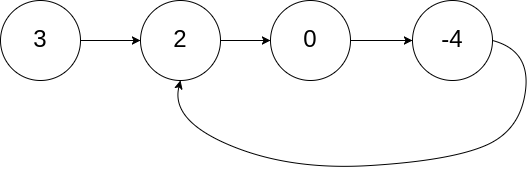
链表中环的入口节点

题目描述：

❝
如果一个链表包含「环」，找出环的入口节点！

示例：输入：head = [3,2,0,-4], 输出： pos = 1 返回索引为 1 的链表节点
❞

分析
1. 判断一个链表「是否有环」：
  
  定义两个指针并同时从链表的「头节点出发」(不涉及append/delete，可以不用dumy节点)
  
  一个指针「一次走一步」，另外一个指针「一次走两步」
  
  如果有环，「走的快」的指针在「绕了n圈」之后将会「追上」走的慢的指针
2. 在①的基础上，快慢指针在某处进行相遇了，此时「调整快慢指针的指向」，「将fast指针指向链表头部」，slow指针保持不变。并且，slow/fast以「相同的速度」(每次移动一个节点)，在slow/fast「再次」相遇时，就是环的入口节点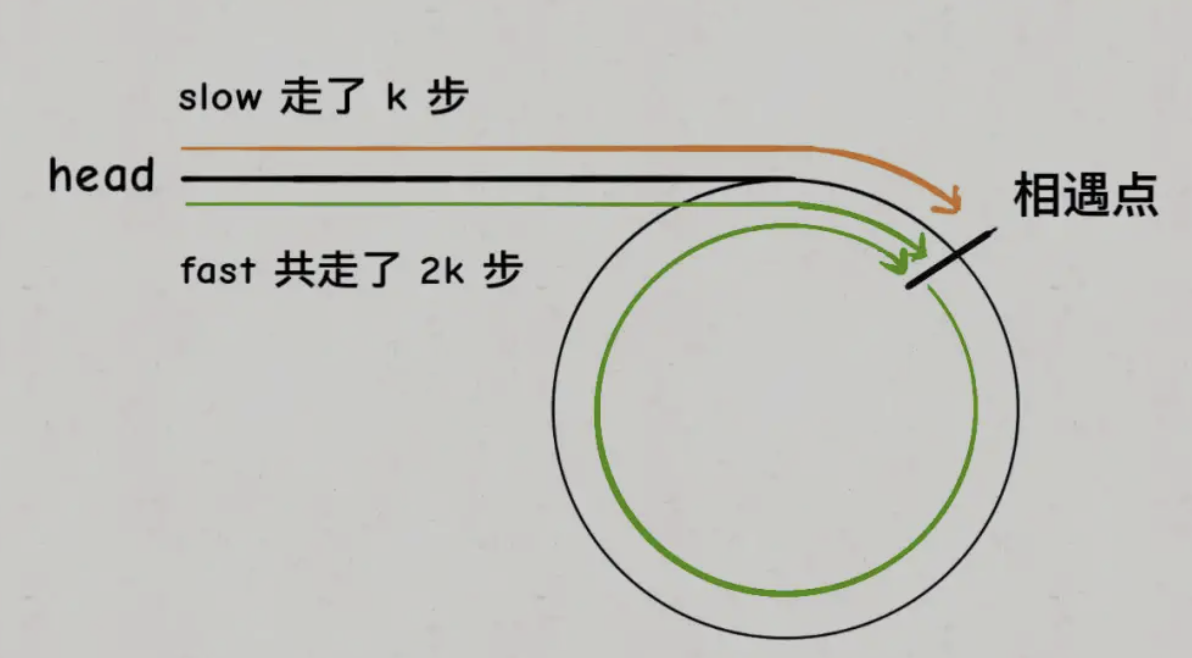
  
  快慢指针相遇点
  
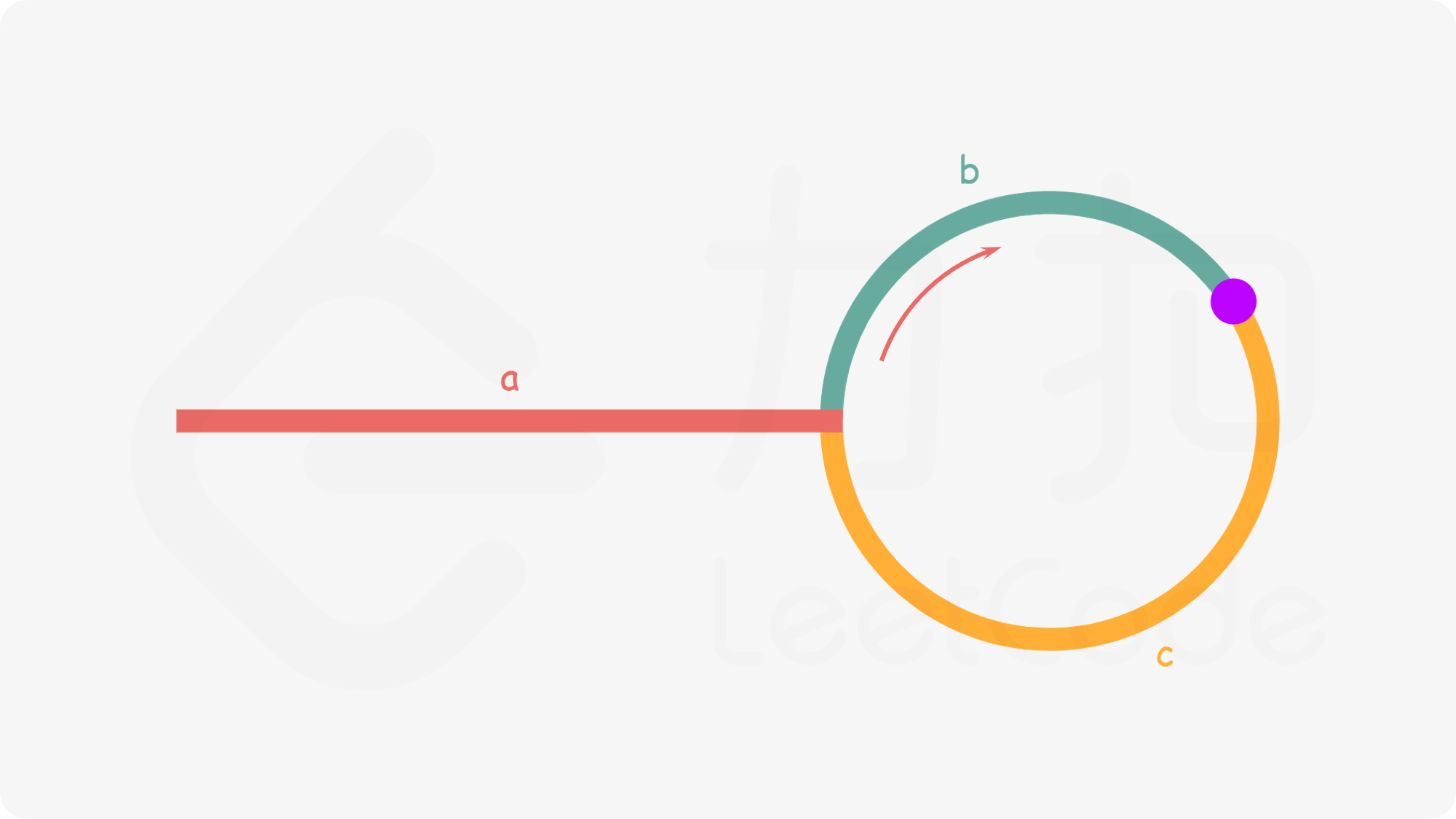  根据快慢指针移动速度之间的关系，并且假设在快指针移动n后相遇，我们可以有
  1. a + n(b+c) + b = a+(n+1)b+nc （「快指针移动的距离」）
  2. (a+b) (「慢指针移动的距离」)
  3. a+(n+1)b+nc=2(a+b)(「快指针比慢指针多移动一倍的距离」)
  4. a=c+(n−1)(b+c)可以得出，如果有两个指针分别从「头节点」和「相遇节点」以「相同的速度」进行移动。在经过n-1圈后，他们会在「环的入口处相遇」
代码实现

「判断一个链表是否有环」
```
function hasCycle(head){
  let fast = head;
  let slow = head;
  
  while(fast && fast.next){
    fast = fast.next.next;
    slow = slow.next;
    if(fast == slow) return true;
  }
  return false;
}
```
「找到环的入口节点」
```
function detectCycle(head){
  let fast = head;
  let slow = head;
  while(fast && fast.next){
    fast = fast.next.next;
    slow = slow.next;
    if(fast ==slow){
      fast = head;
      while(fast!=slow){
        fast = fast.next;
        slow = slow.next;
      }
      return slow
    }
  }
  return null;
}
```
通过对比我们发现，利用双指针查找链表中环的入口节点，其实就是在「判断链表是否有环」的基础上进行额外的处理。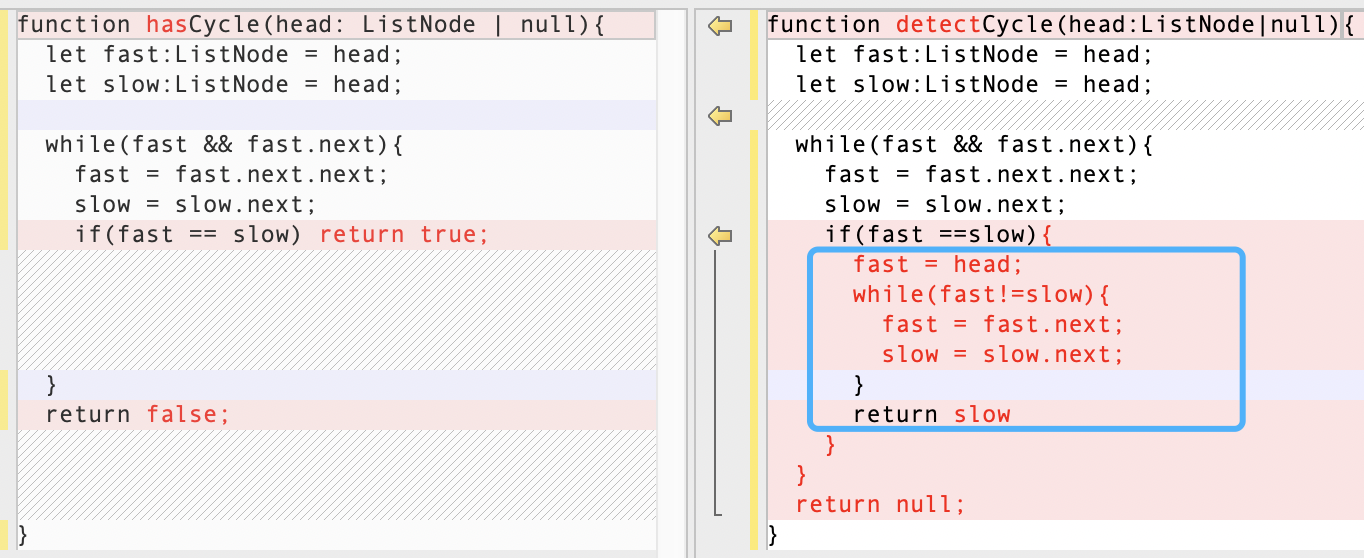

两个链表的第一个重合节点

题目描述：

❝
输入两个「单向」链表，找出它们的「第一个」重合节点

示例：链表A:1->2->3->4->5->6 链表B: 7->8->4->5->6
输出两个链表的第1个重合节点的值是4
❞

分析
1. 如果两个「单向链表」有重合节点，那么这些重合的节点一定「只出现在链表的尾部」。并且从某个节点开始这两个链表的next指针都「指向同一个节点」。
2. 由于涉及到两个链表，此时它们各自的「长度会不一样」，而根据①中我们得知，两个链表相同的节点，都位于各自链表的尾部。
  
  可以利用两个指针分别指向两个链表的头结点
  
  分别遍历对应的链表，计算出对应链表的「节点数量」（count1/count2）
  
  在第二次遍历的时候，节点数多的链表先向前移动distance = Math.abs(count1-count2)个节点
  
  在移动distance个节点后，此时两个链表中「所剩节点数」相同，也就是说，从接下来，可以认为在「两个相同长度的单向链表」中寻找第一个重合节点
代码实现

「计算链表中有多少个节点」
```
function countList(head){
  let count = 0;
  while(head!=null){
    count++;
    head = head.next;
  }
  return count;
}
```
「查找第一个重合节点」
```
function getIntersectionNode(headA, headB) {
  // 计算各自节点数量
  let count1 = countList(headA);
  let count2 = countList(headB);
  
  // 相差节点数
  let distance = Math.abs(count1-count2);
  
  // 找出最长/最短 链表
  let longer  = count1 > count2 ? headA : headB;
  let shorter = count1 > count2 ? headB : headA;
  
  // 定义指向 longer链表的指针
  let node1 = longer;
  // 优先移动distance个节点
  for(let i =0 ;i<distance;i++){
    node1 = node1.next;
  }
  // 定义指向 shorter 链表的指针
  let node2 = shorter;
  // 判断处理
  while(node1!=node2){
    node2 = node2.next;
    node1 = node1.next;
  }
  return node1;
};
```
3. 反转链表

❝
单向链表最大的特点就是其「单向性」--即只能顺着指向下一个节点的指针方向从头到尾遍历。
❞

而有些情况，从链表尾部开始遍历到头节点更容易理解。所以，就需要对链表进行反转处理。

反转链表

题目描述：

❝
将指定的链表反转，并输出反转后链表的头节点

示例：链表:1->2->3->4->5
反转后的链表为5->4->3->2->1, 头节点为5所在的节点
❞

分析
1. 在链表中，i/j/k是3个「相邻的节点」。
  
  原始链表为 a->b->(...)->i->j->k->(...) （...省略了很多节点）
  
  在经过若干次反转操作后，节点i之前的指针都反转了,处理后的节点的next指针都指向前面的一个节点,
  此时，链表结构如下：a<-b<-(...)<-i (断开了) j->k->(...)
  
  将节点j的next指针指向节点i
  此时，链表结构如下：a<-b<-(...)<-i <- j(断开了)k->(...)
2. 节点j的next指针指向了它的「前一个」节点i。此时链表在节点j和节点k之间断开，此时已经反转过的链表，和以节点k为首的链表，「失去了联系」
  
  为了避免链表断开，需要在「调整节点j的next指针之前」把节点k的信息保存起来。即：「保存原始节点的后面信息」
3. 在调整节点j的next指针时，
  
  「事先」保存节点j的「下一个节点」k,以防止链表断开(「暂存后继节点」)
  
  除了需要知道节点j本身，还需要知道「节点j的前一个节点i」 --> j.next = i （「修改引用指向」）
4. 在遍历链表逐个反转每个节点的next指针时需要用到「3个指针」
  
  指向「当前遍历到的节点」：cur (默认值为原链表头节点head)
  
  当前节点的「前一个节点」：prev（默认值为null）
  
  当前节点的「后一个节点」：next(默认值为原链表头结点的下一个节点head.next)
代码实现
```
function reverseList(head){
  // 初始化prev/cur指针
  let prev = null;
  let cur = head;
  // 开始遍历链表
  while(cur!=null){
    // 暂存后继节点
    let next = cur.next;
    // 修改引用指向
    cur.next = prev;
    // 暂存当前节点
    prev = cur;
    // 移动指针
    cur = next;
  }
  return prev;
};
```
重排链表

题目描述：

❝
给一个链表，链表中节点的顺序是l0->l1->l2->(...)->l(n-1)->ln。对链表进行重排处理，使节点顺序变成l0->ln->l1->l(n-1)->l2->l(n-2)->(...)

示例：链表:1->2->3->4->5->6
重排后的链表为1->6->2->5->3->4
❞

分析
1. 通过观察可知，在原链表经过如下处理，即可拼接出重排后链表
  
  链表「一分为二」 第一部分：1->2->3 第二部分：4->5->6
  
  对①的第二部链表，进行「反转处理」 4->5->6-->6->5->4
  
  在②的基础上，从前半段链表和后半段的头节点开始，逐个把它们节点连接起来
  最后的节点顺序为： 1->6->2->5->3->4
2. 「使用双指针来寻找链表的中间节点」
  
  「一快一慢」两个指针「同时」从链表的头节点出发
  
  「快指针」一次顺着next指针方向向前走「两步」
  
  「慢指针」一次「走一步」
  
  「当快指针走到链表的尾节点时候，慢指针刚好走到链表的中间节点」
代码实现

「找到链表的中间节点」（使用快慢指针）
```
function middleNode(head){
        let slow = head;
        let fast = head;
        // 遍历链表节点
        while (fast && fast.next) {
            slow = slow.next;
            fast = fast.next.next;
        }
        // 处理链表节点为偶数的情况
        if(fast){
          slow = slow.next;
        }
        return slow;
    }
```
「合并两个链表」
```
function mergeList(l1,l2){
  let dumy = new ListNode(0);
  let node = dumy;
  while(l1 && l2){
    node.next = l1;
    l1 = l1.next;
    
    node.next = l2;
    l2 = l2.next;
  }
  // 由于l1/l2长度一致
  if(l1) node.next = l1;
  if(l2) node.next = l2;
  return dumy.next;
}
```
「重排链表」
```
function reorderList(head){
  if(head==null) return head;
  
  //找到链表的中间节点
  let mid = middleNode(head);
  // 前半部分链表
  let l1 = head;
  // 后半部分链表
  let l2 = mid.next;
  // 将原链表一分为二
  mid.next = null;
  // 后半部分链表反转
  l2 = reverseList(l2);
  // 合并处理
  mergeList(l1, l2);
}
```
这里省去了链表反转reverseList(前面有对应的代码)

回文链表

题目描述：

❝
判断一个链表是回文链表
要求：时间复杂度为O(n),空间复杂度为O(1)

示例：链表:1->2->3->3->2->1 该链表为回文链表
❞

分析
1. 题目对时间复杂度和空间复杂度都有很高的要求。也就是需要对链表遍历一次，就需要判断链表是否为回文链表
2. 而根据回文的特性可知，从数据的中间「一刀两断」，对某一部分链表进行反转，此时反转后的链表和另外的部分是相同的
  
  找到链表中间节点(「一分为二」)
  
  「反转」某一部分链表
  
  两个链表挨个对比
代码实现

还是熟悉的味道

「找到链表的中间节点」 (前文有介绍，这里不再赘述)

「反转某部分链表」 (前文有介绍，这里不再赘述)

那么，现在就剩下对两个链表进行对比判断了
```
function equails(head1,head2){
  while(head1 && head2){
    //相应位置的val不同，两个链表不同
    if(head1.val!=head2.val){
      return faslse;
    }
    head1 = head1.next;
    head2 = head2.next;
  }
  // 如果head1/head2长度不同，也返回false
  return head1 ==null && head2==null;
}
```
「判断是否为回文」
```
function isPalindrome(head) {
   
    let left = head;
    // 找到链表的中间节点
    let slow = middleNode(head)
    // 反转链表
    let right = reverse(slow);
    // 比较链表
    return equals(left,right)
};
```
后记

「分享是一种态度」。
相关阅读:
IDEA如何打包可运行jar的一个问题。
从一个脚本谈loadrunner的脚本初始化
 explain 用法详解
 linux zip 命令详解
 Jmeter使用——参数化
 Jmeter Constant Throughput Timer 使用
 产生随机时间的例子
 Mysql的列索引和多列索引（联合索引）
Loadrunner负载机agent
Spring context:property-placeholder 一些坑
原文地址：https://www.cnblogs.com/sinferwu/p/16695546.html

算法探险之链表

JS算法探险之链表

文章list

链表-打油诗

文章概要

知识点简讲

链表是个啥

构造链表节点

链表基础算法

1. 链表反转

2. 判断链表是否有环

3. 合并链表

4. 找中点

1. 哨兵节点

简化链表插入操作

简化链表删除操作

2. 双指针

删除倒数第k个节点

分析

代码实现

链表中环的入口节点

分析

代码实现

两个链表的第一个重合节点

分析

代码实现

3. 反转链表

反转链表

分析

代码实现

重排链表

分析

代码实现

回文链表

分析

代码实现

后记

删除倒数第`k`个节点