摘要:使用canvas实现可交互的3D魔方
一、简单分析
魔方物理性质:
1.中心块(6个):中心块与中心轴连接在一起,但可以顺着轴的方向自由的转动。
2.棱块(12个):棱块的表面是两个正方形,结构类似一个长方体从立方体的一个边凸出来。
3.角块(8个):角块的表面是三个正方形,结构类似一个小立方体从立方体的一个边凸出来,这样的结构可以让角块嵌在三个棱块之间。
4.可见方块(26个):魔方对于我们可见的方块有26块。
5.魔方六个面,每个面九个方块,转动时每个面绕着自己面的中心块旋转。
6.在观察魔方时,我们将整个魔方绕着三维空间中的某个点旋转
7.在人的视野范围内,魔方可见的部分只有三个面,19个方块。
二、实现方式
1)完成方块的旋转
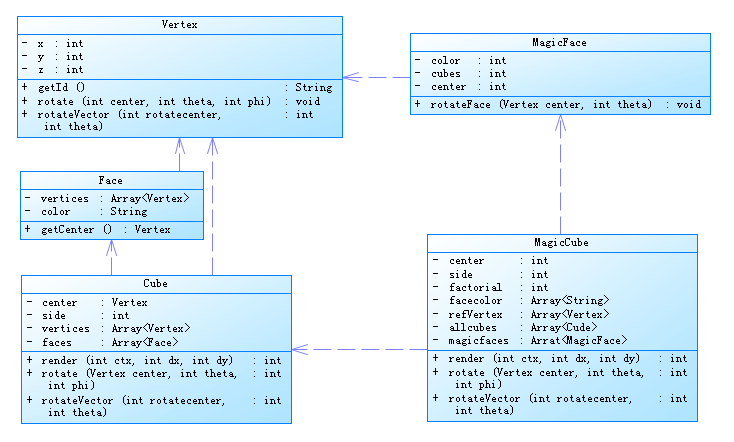
通过简略的类图,先了解一下实现的思路。在一个三维空间中,最基础的就是点(Vertex),点组成了面(Face),面组成了空间立方体(Cube)。魔方(MagicCube)由26个Cube组成,同时将26个Cube单组不重复的分为6组(MagicFace)。当旋转观察魔方时,26个Cube绕着魔方的中心旋转。当转动魔方的某一面时,MagicFace上所有的Cube围绕以原点为起点,面的中心为终点的矢量旋转。只需要掌握点在空间中的旋转,即可完成整个魔方的旋转。三维空间中点的旋转主要用到了数学上的旋转公式。关于如何将一个三维空间的立方体投影到平面并实现旋转请看我的上一篇随笔。
2)完成方块的上色
第一步只是完成了一个透明魔方旋转。我们需要给魔方上色。初始化时为每个cube的face上色,我们不可见的面设置为白色。就像我们在现实中绘画一样,在canvas上绘制图像时后渲染的图像会把之前的覆盖掉,因此魔方的渲染顺序我们需要从后往前渲染。
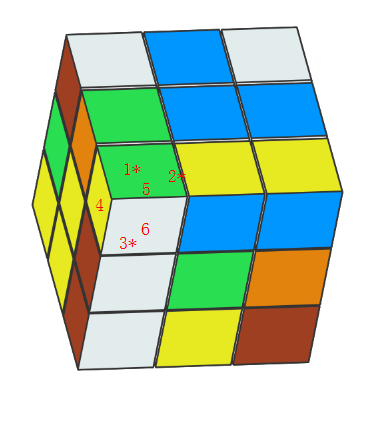
我们通过面的中心距离原点的Y值(本例以Y轴垂直与屏幕作为参考轴),来确定渲染顺序。单个方块的渲染如上图,6个面(*代表看不见的面),渲染顺序为1*,2*,3*,4,5,6,后渲染的面将前面渲染的面盖住。
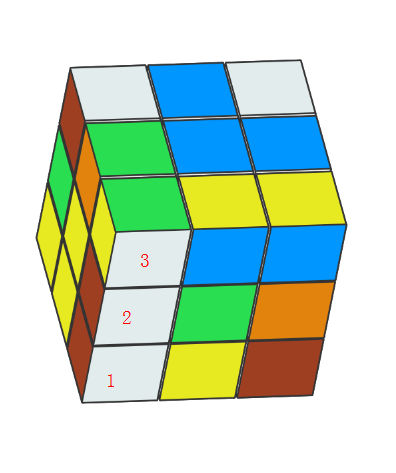
整个魔方的渲染,举例标了数字的三个方块,也是通过方块中点距离原点的Y值来确定渲染顺序。渲染顺序先是方块1,然后方块2把1的上半部分盖住,然后方块3把方块二的上半部分盖住。
3)完成鼠标的点击事件
交互是本例中比较难的一个点,canvas 没有提供为其内部元素添加事件监听的方法,因此如果要使 canvas 内的元素能够响应事件,需要自己动手实现。通过获得鼠标在 canvas 上的坐标,计算当前坐标在哪些元素内部,然后对元素进行相应的操作。配合自定义事件,我们就可以实现为 canvas 内的元素添加事件监听的效果。

在上图中,可旋转的面投影到二维平面的区域共有6个,图中只标识了三个。如何确定投影的区域呢?想了很多方法,最终采用了建立参考点的方法。
1.获取到3个可视面MagicFace(F1F2F3)---6个面中中心Y值最大的3个
2.获取到3个可视面无穷远的参考点(V1V2V3)--6个参考点中Y值最大的3个
4.我们循环6个面,例如循环到图中的F2面,我们过滤离F2中心最近的参考点(过滤掉与F2中心空间距离最小的点),剩下V1V3
5.获取到F2面中离V1最最近的三个方块(即上方红色区域的三个方块) -- 离参考点的空间距离
6.获取三个方块中里F2这个面中点最远的4个点(即上方红色区域的4个顶点)
通过3层循环,即可获取到所有可视面的投影。当我们鼠标点击并滑动一段距离时(图中黑点),我们就可以判断两个点所在的投影的位置是哪一个面的,获取到面之后就可以旋转那个面。
PS:我们通过建立参考点,6个无穷远的点(分别在X,Y,Z轴的正负方向上,魔方整体旋转时参考点也会旋转)。使用他与各个元素中点的距离用于判断一些特殊位置的点和面的方法。滑动部分的投影的8个点就是用参考点辅助求出的。
判断点是否在面中使用的是pnpoly算法 https://wrf.ecse.rpi.edu//Research/Short_Notes/pnpoly.html
三、最终效果

PS:面积投影越小事件效果就不灵敏了,有待优化