前言
OO第一单元共有三次作业,分别为多项式求导、带有三角函数与幂函数的表达式求导、带有嵌套表达式因子的表达式求导。虽然这三次作业都离不开求导,可是每次作业的复杂度都是大大递增的。对于习惯于面向过程编程的我来说,完成这三次作业是一个不小的挑战。我在各个方面也还存在着诸多问题,借由此次博客,我将回顾一下完成这三次作业的经历,并对代码进行一次详细的分析与总结。
基于度量的程序结构分析
这里使用了IDEA的Diagram和MetricsReloaded工具辅助分析。工具里的一些参数说明如下:
方法与类的复杂度分析(Complexity Metrics)
1、方法
(1)、ev(G):即Essential Complexity,用来表示一个方法的结构化程度,范围在[1,v(G)]之间,值越大则程序的结构越”病态“。
(2)、iv(G):即Design Complexity,用来表示一个方法和他所调用的其他方法的紧密程度,范围在[1,v(G)]之间,值越大联系越紧密。
(3)、v(G):即循环复杂度,可理解为穷尽程序流程每一条路径所需要的试验次数。
2、类
(1)、OCavg:表示类的方法的平均循环复杂度
(2)、WMC:表示类的方法的总循环复杂度
类之间的依赖度分析(Dependency Metrics)
(1)、Cyclic:指和类直接或间接相互依赖的类的数量,这样的相互依赖可能导致代码难以理解和测试
(2)、Dcy和Dcy*: 计算了该类直接依赖的类的数量,带*表示包括了间接依赖的类。
(3)、Dpt和Dpt*:计算了直接依赖该类的类的数量,带*表示了包括了间接依赖的类
第一次作业
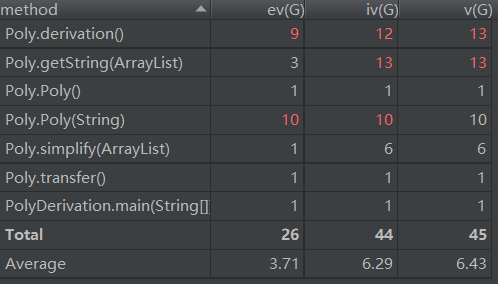
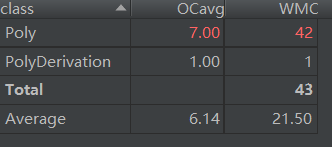
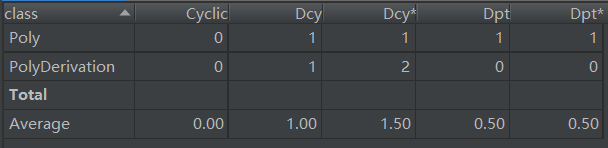
可以看到,在第一次作业中,ev(G)和v(G)都比较高,主要是因为第一次作业我没有用大正则直接进行匹配,而是采用了特判的方法,将所以可能的格式错误判断出来,由于要进行多次判断,因而复杂度较高。这种特判的方法构成的代码可拓展性较差,而且非常容易漏掉某些情况导致BUG,因此在之后的作业中我舍弃了这个方法。
第二次作业
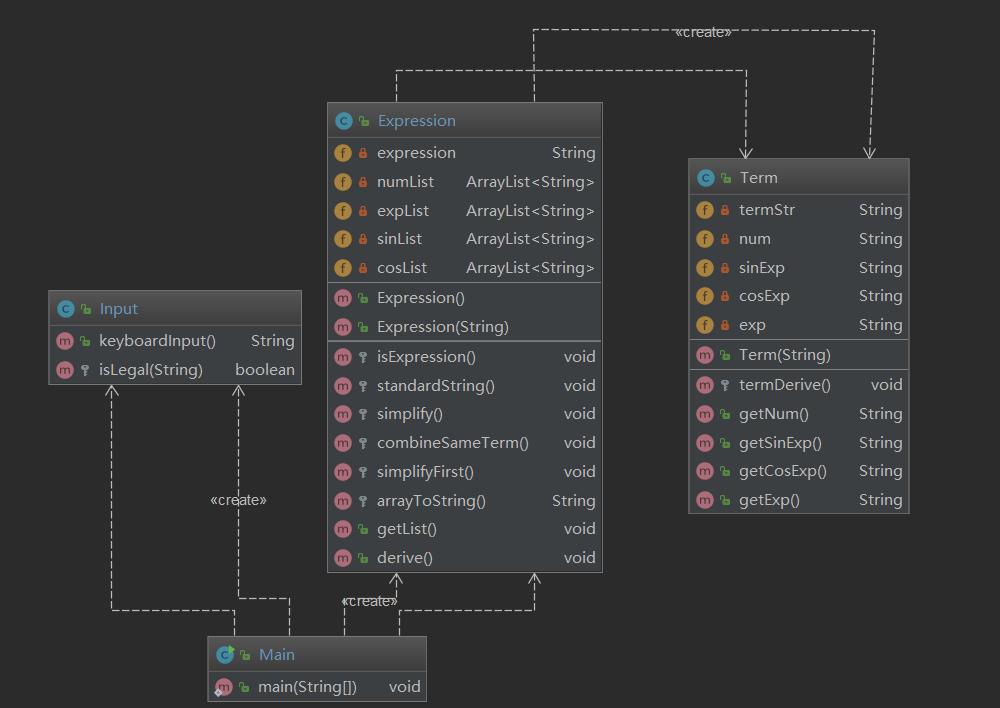
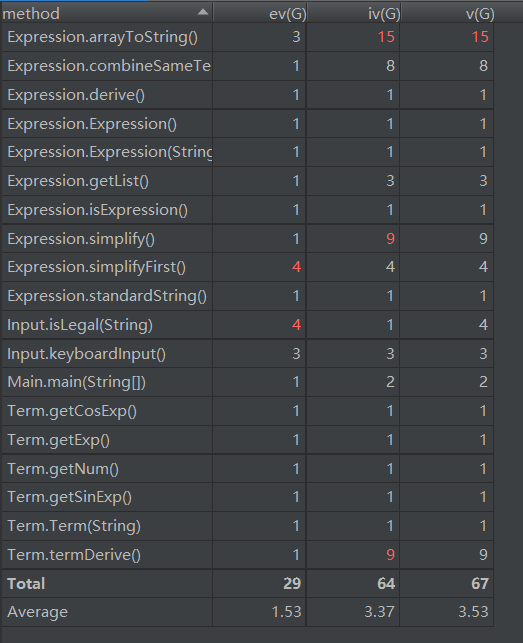
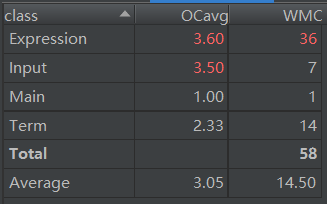
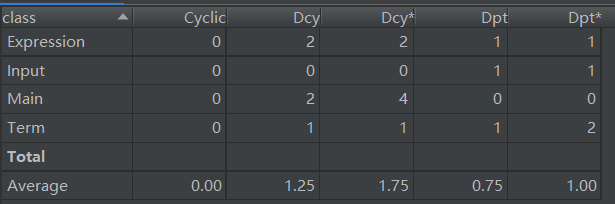
第二次作业的情况较第一次来说要好了许多,但是Input.isLegal()等方法的ev(G)依然很高,主要是因为这些方法中采用了较多层的if-else结构或者for循环,而且高耦合的问题依然存在
第三次作业
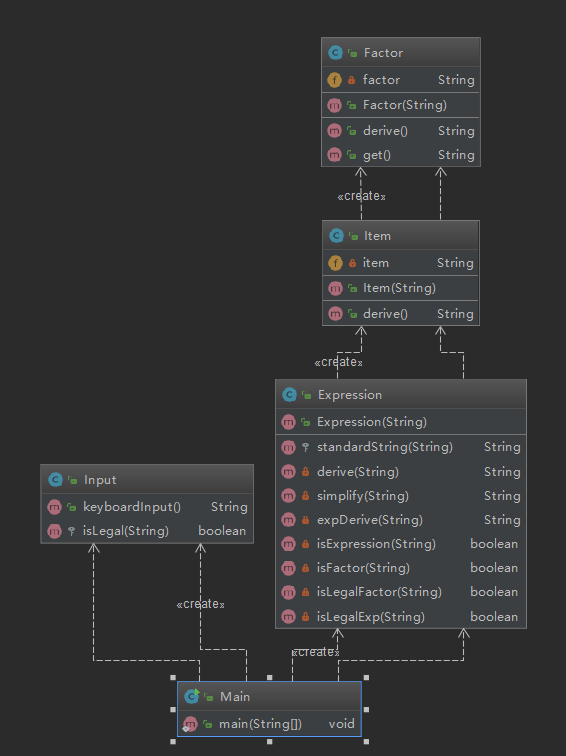
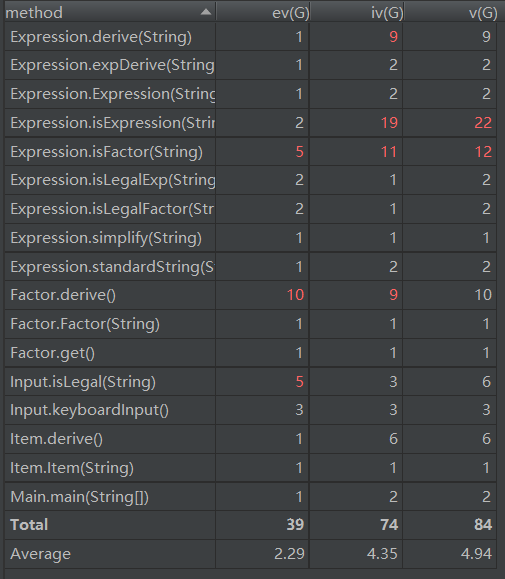
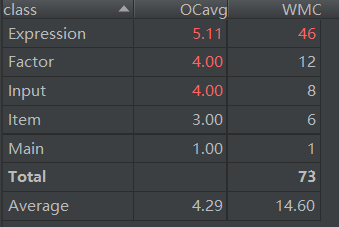

可以看出,第三次作业的设计非常糟糕,主要是未能好好考虑代码架构问题。我只是为了能够完成测试而写代码,而没有充分考虑代码的层次与结构问题,这导致每个类的规模较大,实现的方法数量较多,类的复杂度也较高,这样的代码难以进行维护和扩展,我也未能灵活使用继承和接口来实现,这是此次作业的不足之处。
根据以上三次作业的代码分析结果,我的代码编写受着面向过程思想的影响较深,没有应用到面向对象的一些思想,例如继承和接口等。此外,从代码的组织上来看,每一次作业我基本上都是直接重构,很少用到了源代码,这也体现我的代码可拓展性较差。希望在以后的作业中加以改进。
分析自己程序的bug
第一次作业
第一次作业的BUG主要在于对JAVA一些String类的方法不熟悉导致的。例如String.split()方法,当分隔符在字符串开头时,所得字符串数组第0项为空字符串,当分隔符在字符串末尾时,所得字符串数组最后一项却不是空字符串。由于对方法不熟悉,导致我未能正确判断处于字符串末尾的分隔符,导致BUG
第三次作业
第三次作业的BUG在于正则表达式,在编写正则表达式时,忽略了表达式因子括号前可以存在2个运算符的情况,从而导致类似+ - (EXP)形式的输入会被判定为WRONG FORMAT
找他人的bug
第一次作业由于代码量较少,阅读起来比较简单,我秉着学习的目的去阅读了他人的代码,同时思考他人的设计思路等等,通过这样我找出了一些不容易被查出的BUG。同时,我自己编造了一些较为刁钻的数据,也可以找出不少人的BUG
在后两次作业中,我主要是通过观察代码的架构,例如对方设计了什么类,来实现什么样的功能,由此编造一些在实现过程中可能出现的边界情况,由此寻找BUG
Applying Creational Pattern
在第一次作业中,我直接把整个表达式作为一个类进行求导
在第二次作业中,我把一个表达式类又进行了细分,即一个表达式类由若干个项类构成,而项类又由若干个因子类构成,通过对因子求导,实现项的求导,通过项的求导,实现表达式的求导
在第三次作业中,我同样采用了第二次作业的结构,只是由于表达式因子的存在,我先将表达式因子都替换为一个(exp)因子,再进行正则表达式匹配替换后的表达式是否满足条件,同时通过递归,判断被替换的表达式因子内部是否满足表达式,通过这种方式实现了表达式的合法性判断及求导