《Natural Image Stitching with the Global Similarity Prior》论文笔记(一)
@(sinbad)[360sinbad@gmail.com]
简要记录下基于网格优化的图像对齐方法算法的流程步骤,以便日后记忆。
全局单应性VS网格优化
2D图像拼接常利用相机做纯旋转运动或者拍摄场景为平面场景的前提假设对模型进行单应性近似,从而得到图像之间的映射关系。图像对齐时仅仅利用全局单应性往往不够。2011年后陆续出来基于网格优化的图像对齐方法。其中,APAP方法利用多个局部单应性来实现精确对齐,但是在图像变换的约束上仅有局部单应性容易造成图像畸变,使得图像质量变差。GSP方法提出相似性变换优先的思想,利用相机运动模型估计分解出合理的尺度因子和2D旋转角,从而约束了图像变形,可以得到表现更为自然的拼接图像。再结合局部相似性优化项,从而更为通用地解决了图像精确对齐问题。在实际应用中,使用最广泛的两个方向应该是在手机上的全景图像拼接和最近比较火的视频防抖。我估计全景拼接之前都是以opencv的拼接算法为原型,参考论文为 Automatic Panoramic Image Stitching using Invariant Features基于全局单应性变换,然后对重叠边界进行金字塔融合,手机上可以参考google原生相机的全景拼接。不知从哪款手机开始,全景拼接开始重新被定义,网上搜了下全景拼接算法提供商TOP class --日本morpho最为出名估计是用的网格优化方案。
算法流程
- [ ] 特征检测及匹配
- [ ] 图像两两匹配图验证
- [ ] APAP方法生成匹配点
- [ ] 焦距估计和3维旋转角估计
- [ ] 尺度和旋转角估计
- [ ] 网格优化
- [ ] 纹理映射合成结果图
GSP算法简介
算法思想主要是将图像网格化变形,通过特征对齐的方式约束重叠区域,通过全局相似性平滑非重叠区域,另外在局部相似约束下,保证图像拼接自然减少畸变。本篇主要从网格优化的能量函数分析,针对能量函数各个优化项的构造具体分析,方便理解。
总的能量代价函数论文中为:
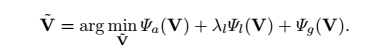
式中,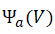 为对齐误差项,
为对齐误差项, 为局部相似项,
为局部相似项, 为全局相似项,
为全局相似项, 为局部相似项权重参数。
为局部相似项权重参数。
对于两个互有重叠的图像 ,将图像网格化并使用向量
,将图像网格化并使用向量
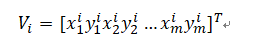
表示图像I的网格顶点坐标,其中m为顶点个数。两个图像顶点坐标可表述为
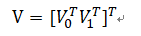
对齐项:

我们知道对齐大多会想到特征匹配,但这里不是使用匹配后的feature point而是APAP论文中提出的matching point坐标作为对齐输入。效果见下图。

Tips:相对于feature points在图像中的分布,matching points就均匀很多。matching points对应的是网格顶点,(?)具体是网格顶点还是网格quad的中心点得细看下代码。如何生成需要看论文APAP中的介绍。核心思想也是在图像网格化基础上,对每一个网格求解局部独立单应性矩 。局部独立单应性矩求解方法跟单个全局单应性矩的求解方法相似,只是对单个全局单应性矩前加了一个系数矩,因此单个全局求解单应性矩的方法叫DLT,局部
。局部独立单应性矩求解方法跟单个全局单应性矩的求解方法相似,只是对单个全局单应性矩前加了一个系数矩,因此单个全局求解单应性矩的方法叫DLT,局部 的求解就叫做Moving DLT.两者的求解详情放在了文章后面。
的求解就叫做Moving DLT.两者的求解详情放在了文章后面。
对齐项表述的约束原理网上找了两张图说明比较形象,但又有点出入。
另外一个参考说明。

两者的区别在于第一个是当求解 图像变形后的网格时,设
图像变形后的网格时,设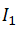 网格做warp得到的新的feature point坐标为未知,
网格做warp得到的新的feature point坐标为未知, 网格做warp后feature point坐标点为测量值计算最小误差。同理反过来求解
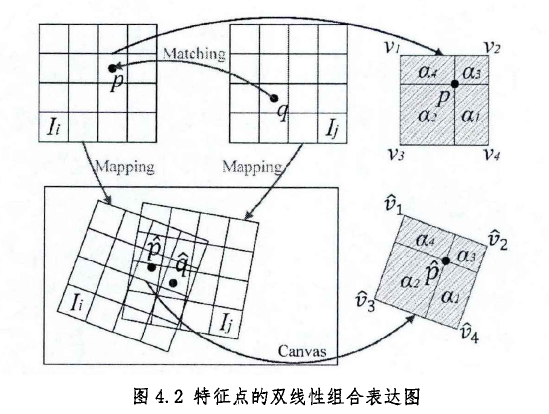
网格做warp后feature point坐标点为测量值计算最小误差。同理反过来求解 图像变形后的网格。由于优化的是网格顶点(matching point),因此,将特征点表达成其所有网格的四个顶点的双边线性组合:
图像变形后的网格。由于优化的是网格顶点(matching point),因此,将特征点表达成其所有网格的四个顶点的双边线性组合: 。
。
其中, 代表各自所占的面积比重,例如:p越靠近
代表各自所占的面积比重,例如:p越靠近 远离
远离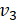 ,则
,则 越大,而
越大,而 越小。而变换后的特征点表达为:
越小。而变换后的特征点表达为: ,其中
,其中 变换前后保持不变。
变换前后保持不变。

求解方法上,对齐项可以简化为 求解线性方程组。
求解线性方程组。 表示在顶点集
表示在顶点集 下的雅可比矩阵。所以
下的雅可比矩阵。所以 为其所在网格4个顶点差值权值矩阵。
为其所在网格4个顶点差值权值矩阵。
补充说明1.
*1.单个全局单应性
图像q到p的单应性近似模型表达为

矩阵表达形式为
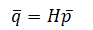
对公式进行展开可以得到两个线性方程,如下公式

对公式进行直接线性变换(DLT, Direct Linear Transformation),将带估计的单应性矩阵H转变成变量向量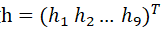 ,同时将匹配特征点对p与q的已知变量关系转换已知线性变量矩阵
,同时将匹配特征点对p与q的已知变量关系转换已知线性变量矩阵
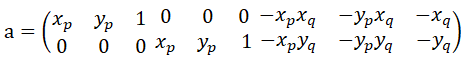
因而可以得到如下公式
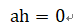
通常,在两幅图像图像上可以有着上百或者上千对的匹配特征点对。因而,实际上在求解h时通常是通过使得累积平方和误差最小来评估(最小二乘法),如下公式所示。
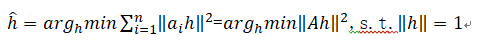
此处,上式是一个超定方程的最小二乘解(当n>4时)。其利用‖h‖=1来限制h的自由度为8,其中 。其表示所有
。其表示所有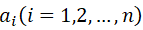 的纵向排列,大小为2n×9。
的纵向排列,大小为2n×9。
通常,利用SVD分解A矩阵,则可以很容易地获得最小二乘解 ,其值为最小奇异值对应的特征向量。事实上,为了避免误匹配带来的影响,通常也可以利用RANSAC结合单应性评估的四点法(最小采样四个匹配特征点对,通常为了保证高置信度,就仅采样四个匹配特征点对),来求解问题。
,其值为最小奇异值对应的特征向量。事实上,为了避免误匹配带来的影响,通常也可以利用RANSAC结合单应性评估的四点法(最小采样四个匹配特征点对,通常为了保证高置信度,就仅采样四个匹配特征点对),来求解问题。
*2. 多个局部单应性
为了获得多个局部单应性,首先将图像进行网格划分。然后,根据每对匹配特征点对距离当前网格中心点的远近来进行加权,从而评估加权平方和误差最小,如下公式所示:
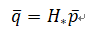
进而

m表示网格个数,需要评估m个局部单应性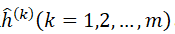 。矩阵
。矩阵 是权重
是权重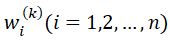 的对角组合
的对角组合
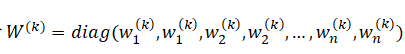
另外,权重

其中,点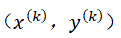 表示查询图上第k个网格的中心点,点
表示查询图上第k个网格的中心点,点 表示查询图像上第i个特征点,参数σ是高斯函数的尺度因子,参数γ是一个阈值参数。该公式表明:一、特征点越靠近网格中心,则其对当前网格单应性估计的贡献越大;二、由于实际中多数特征点都是远离网格中心的,其权重趋近于0,为了避免这些特征点的贡献消失,设置阈值参数γ用于确立最小权重不低于该阈值。
表示查询图像上第i个特征点,参数σ是高斯函数的尺度因子,参数γ是一个阈值参数。该公式表明:一、特征点越靠近网格中心,则其对当前网格单应性估计的贡献越大;二、由于实际中多数特征点都是远离网格中心的,其权重趋近于0,为了避免这些特征点的贡献消失,设置阈值参数γ用于确立最小权重不低于该阈值。
另外,可以看到:假如 ,则
,则 退化成单位矩阵,于是,所有的局部单应性估计结果都会退化成全局单应性。从这个角度来看,阈值参数γ代表着局部单应性往全局单应性的趋近程度。
退化成单位矩阵,于是,所有的局部单应性估计结果都会退化成全局单应性。从这个角度来看,阈值参数γ代表着局部单应性往全局单应性的趋近程度。