计算频繁项集:
首先生成一个数据集
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

测试数据集dataset有了,第一步,我们要根据数据集dataset得到一个集合C1,集合C1中包含的元素为dataset的无重复的每个单元素,候选项集。
def createC1(dataset):
C1 = []
for transaction in dataset:
for item in transaction:
if not [item] in C1:
C1.append([item])
C1.sort()
return map(frozenset, C1)
返回的数据map计算得到一个元素为frozenset的集合。
为什么要转成frozenset?

原因两个:
1. 这个集合是从dataset中抽取出所有无重复的数据集,是固定的,应该是不可变的类型。
2. frozenset可以作字典
可以看一下返回结果:
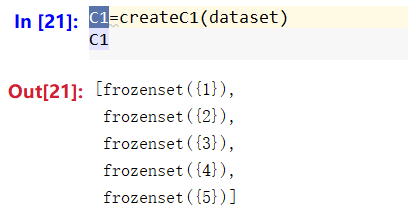
第二步,计算C1<key>每个元素key的支持度。
支持度= count(key) / sizeof(C1)
def scanD(D, Ck, minSupport):
ssCnt = {}
for tid in D:
for can in Ck:
if can.issubset(tid):
if not ssCnt.has_key(can):
ssCnt[can] = 1
else:
ssCnt[can] += 1
numitems = float(len(D)) # 数据集长度
retList = []
supportData = {}
for key in ssCnt:
support = ssCnt[key] / numitems
if support >= minSupport:
retList.insert(0, key)
supportData[key] = support
return retList, supportData
调用返回结果:
先把dataset转成元素为集合的类型。
这里设置支持度为0.5。当key在dataset中出现的集合个数超过一半即认为是频繁项。
L1是根据计算C1中每个元素是否满足支持度规则过滤得到的C1的子集。
L1的元素两两组合构成C2,再根据C2中每个元素是否满足支持度规则过滤得到的C1的子集L2。依次类推,直到Lk是单元素集合。
添加如下代码,可以得到一个完整的找频繁项集的代码:

def aprioriGen(Lk, k):
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i + 1, lenLk):
L1 = list(Lk[i])[:k - 2];
L2 = list(Lk[j])[:k - 2]
L1.sort()
L2.sort()
if L1 == L2:
retList.append(Lk[i] |
Lk[j])
return retList
def apriori(dataset, minsupport=0.5):
C1 = createC1(dataset) # 候选项集
D = map(set, dataset) # 数据集
L1, supportData =
scanD(D, C1, minsupport) # 频繁项集与支持度
L = [L1]
k = 2
while (len(L[k - 2]) > 0):
Ck = aprioriGen(L[k - 2], k)
Lk, supK = scanD(D, Ck,
minsupport)
supportData.update(supK)
L.append(Lk)
k += 1
return L, supportData
apriori是主函数,这里对Lk进行了合并,如果Lk的两个元素(都是集合,假设分别是Lk1,Lk2)的[0:k-2]是一样的,(k是什么?k是Lk1的长度加1)比方说:
example1:
{a},{c} k=2
[0:k-2]分别是{}=={},需要进行合并。得到{a,c}
注意:[0:0]意思是从0开始取(含0),直到0(不含0),所以是{}
example2:
{a,c},{a,d} k=3
[0:k-2]分别是{a}=={a},合并得到{a,c,d}
注意:[0:1]意思是从0开始取(含0),直到1(不含1),所以是{a}
应该能理解怎么合并的了。
为什么要合并?
上面解释了怎么合并,以及合并的规则。我们拿到的数据是由C1生成的L1,L1是单元素中符合支持度的构成的集合。所以我们只需要对L1进行组合,就能得到二元素集合C2,并根据支持度过滤得到其中符合支持度的二元素的频繁项集L2。由L1得到C2,这就是为什么要合并的理由。
为什么用这种合并规则呢?
L1={[frozenset([1]), frozenset([3]),
frozenset([2]), frozenset([5])]}
很明显,我们可以组合得到
Ck[k=2]={[frozenset([1, 3]), frozenset([1, 2]), frozenset([1, 5]), frozenset([2, 3]), frozenset([3, 5]), frozenset([2, 5])]}
scanD(D, Ck, minsupport)执行该函数得到我们想要的
Lk[k=2]= {[frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])]}。
接着看:
接下来我们就要对Lk[k=2]进行组合了。按照我们的规则:
[1,3]没有与之可以合并的。
[2,5][2,3]可以合并。得到[2,3,5]
[3,5]没有与之合并的。
所以Ck[k=3]={[frozenset([2, 3, 5])]}
假如我们不按照该规则来:
[1,3][2,5]=>[1,2,3,5],三元素集合这点规则是必须要遵守的。
[1,3][2,3]=>[1,2,3]出现[1,2]该子集不满足支持度。
[1,3][3,5]=>[1,3,5]出现[1,5]该子集不满足支持度。
[2,5][2,3]=>[2,3,5]
[2,5][3,5]=>[2,3,5]
[2,3][3,5]=>[2,3,5]出现三个重复的[2,3,5],还需要我们添加去重规则,相对比较麻烦。而且按照我们的规则,可以减少集合的数目,省去遍历去重的过程,降低算法的时间复杂度。
根据规则生成的Ck,是建立在不违背最小支持度的基础之上的,至于生成的Ck是否符合最小支持度,接下来要使用scanD算法来进行验证,并丢掉不符合最小支持度的项集。
有一个问题:
k-2的操作,到底是怎么做到的,避免出现类似[1,2,3]这种含有[1,2]子集是之前已经被抛弃的集合。还是说,这里就是一个巧合?。
挖掘关联规则:
1. # 下面是关联规则 默认最小置信度为0.7
2. # 主函数
3. def generateRules(L, supportData, minConf=0.7):
4. bigRuleList = []
5. for i in range(1, len(L)): # 不处理单元素集合L[0]
6. for freqSet in L[i]:
7. H1 = [frozenset([item]) for item in freqSet]
8. if (i > 1): # 当集合中元素的长度大于2的时候,尝试对集合合并。
9. # 比如:[2,3,5]=>{[2,3],5}
10. rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
11. else: # 对于2元组,直接计算置信度
12. calConf(freqSet, H1, supportData, bigRuleList, minConf)
13. return bigRuleList
14.
15.
16.def calConf(freqSet, H, supportData, brl, minConf=0.7):
17. prunedH = []
18. for conseq in H:
19. conf = supportData[freqSet] / supportData[freqSet - conseq] # 置信度
20. if conf >= minConf:
21. print freqSet - conseq, "--->", conseq, "conf", conf
22. brl.append((freqSet - conseq, conseq, conf))
23. prunedH.append(conseq)
24. if (len(freqSet) > 2):
25. conf = supportData[freqSet] / supportData[conseq] # 置信度
26. if conf >= minConf:
27. print conseq, "--->", freqSet - conseq, "conf", conf
28. brl.append((conseq, freqSet - conseq, conf))
29. prunedH.append(freqSet - conseq)
30. return prunedH
31.
32.
33.def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
34. m = len(H[0])
35. if (len(freqSet) > (m + 1)):
36. Hmp1 = aprioriGen(H, m + 1)
37. Hmp1 = calConf(freqSet, Hmp1, supportData, brl, minConf)
38. if (len(Hmp1) > 1):
39. rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
40.
41.
42.ruleList = generateRules(L, supportData)
43.# print ruleList
对rulesFromConseq解释一下:
在主函数generateRules中的标记处,此时freqSet是三元组[2,3,5],尝试对其元素进行合并。调用rulesFromConseq,执行aprioriGen(H, m + 1)得到Hmp1={[frozenset([2, 3]), frozenset([2, 5]),
frozenset([3, 5])]}
然后调用calConf计算置信度。
这里对calConf补充了如下代码:
1. if (len(freqSet) > 2):
2. conf = supportData[freqSet] / supportData[conseq] # 置信度
3. if conf >= minConf:
4. print conseq, "--->", freqSet - conseq, "conf", conf
5. brl.append((conseq, freqSet - conseq, conf))
6. prunedH.append(freqSet - conseq)
理由:原代码,如果freqSet =[2,3,5] H={[frozenset([2, 3]), frozenset([2, 5]), frozenset([3, 5])]}
[2,3,5]去计算对[2][3][5]的置信度均不符合最小要求,返回[],无法继续对[2,3][2,5][3,5]进行置信度验证。
源代码:https://files.cnblogs.com/files/simuhunluo/Apriori%E7%AE%97%E6%B3%95%E4%BB%A3%E7%A0%81.zip