题目:
给定一个字符串 (s) 和一个字符模式 (p)。实现支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符。 '*' 匹配零个或多个前面的元素。
匹配应该覆盖整个字符串 (s) ,而不是部分字符串。
说明:
s可能为空,且只包含从a-z的小写字母。p可能为空,且只包含从a-z的小写字母,以及字符.和*。
示例 1:
输入: s = "aa" p = "a" 输出: false 解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入: s = "aa" p = "a*" 输出: true 解释: '*' 代表可匹配零个或多个前面的元素, 即可以匹配 'a' 。因此, 重复 'a' 一次, 字符串可变为 "aa"。
示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入: s = "aab" p = "c*a*b" 输出: true 解释: 'c' 可以不被重复, 'a' 可以被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入: s = "mississippi" p = "mis*is*p*." 输出: false
思路:
这是一个经典的动态规划问题,在面试中经常考到,值得反复练习~
首先确定状态,我们定义dp[i][j]:代表字符串s[0~(i-1)]和字符串p[0~(j-1)]的匹配状态,如果dp[i][j]==1,则说明s[0~(i-1)]能被p[0~(j-1)]匹配,反之,当dp[i][j]==0,则说明 s[0~(i-1)]不能被p[0~(j-1)]匹配。
接下来是初始化问题,dp[0][0]代表字符串s和字符串p都是空串,空串和空串肯定是能匹配的,所以dp[0][0] = 1;当只有字符串p是空串时,这时的字符串s和字符串p肯定是无法匹配的,所以dp[0.....n][0]=0;当只有字符串s是空串时,我们看下图的初始情况,“ab",”a*c*ab",其中“a*”,将会变成一个空串,所以在dp[0][2] = 1 ,它是由dp[0][0]决定的,这是一个状态转移,即当p[j-1] == '*'时,dp[0][j]=dp[0][j-2]。
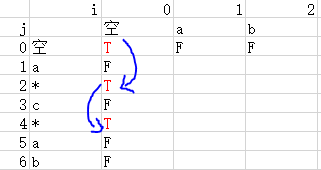
最后考虑状态转移,
- 当指针指向的两个字符相等时,即s[i-1]==p[j-1]或者p[j-1]=='.'(因为'.'可以匹配任意单字符),只有当dp[i-1][j-1]是匹配的,dp[i][j]才是匹配的,如下图中蓝色的位置,状态转移方程为 dp[i][j] = dp[i-1][j-1]

2.当指针指向字符串p的‘*’时,即p[j-1]=='*'时,分两种情况
①s[i-1]!=p[j-2]&&p[j-2]!='.',也就是“kac","kb*ac",说明此时”b*“应该是一个空串,当是空串的转移方程前面提到过,dp[i][j]=dp[i][j-2]
②s[i-1]==p[j-2]||p[j-2]=='.',此时的”*“可以匹配0个,一个,多个前面的元素
a.当"*"匹配前面0个元素,也就是空串喽~dp[i][j]=dp[i][j-2]
b.当”*“匹配前面一个元素时,也就是“a","a*"这种情况,只要字符串s”*“前面的匹配了就可以,状态转移为dp[i][j]=dp[i][j-1]
c..当”*“匹配前面多个元素时,也就是“aaaa","a*"这种情况,状态转移为dp[i][j]=dp[i-1][j]
代码:
class Solution { public: bool isMatch(string s, string p) { int n = s.length(); int m = p.length(); int dp[n+1][m+1]; memset(dp,0,sizeof(dp)); dp[0][0] = 1; for(int i=2;i<=m;i++) { if(p[i-1]=='*' && dp[0][i-2]==1) { dp[0][i] = 1; } } for(int j=1;j<=m;j++) { for(int i=1;i<=n;i++) { if(s[i-1]==p[j-1] || p[j-1]=='.') { dp[i][j] = dp[i-1][j-1]; } else if(p[j-1]=='*') { if(s[i-1]!=p[j-2]) dp[i][j] = dp[i][j-2]; if(s[i-1]==p[j-2]||p[j-2]=='.') dp[i][j] = dp[i][j-1] + dp[i-1][j] + dp[i][j-2]; } } } return dp[n][m] != 0 ; } };