参考文献:https://baijiahao.baidu.com/s?id=1609320767556598767&wfr=spider&for=pc
三者都是对数据进行预处理的方式。
标准化(Standardization)
归一化(normalization)
正则化(regularization)
归一化(MinMaxScaler)
将训练集中某一列数值特征(假设是第i列)的值缩放到0和1之间。方法如下所示:
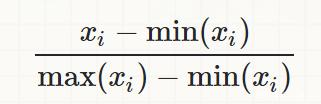
我们在对数据进行分析的时候,往往会遇到单个数据的各个维度量纲不同的情况,比如对房子进行价格预测的线性回归问题中,我们假设房子面积(平方米)、年代(年)和几居室(个)三个因素影响房价,其中一个房子的信息如下:
- 面积(S):150 平方米
- 年代(Y):5 年
这样各个因素就会因为量纲的问题对模型有着大小不同的影响,但是这种大小不同的影响并非反应问题的本质。
为了解决这个问题,我们将所有的数据都用归一化处理至同一区间内。
标准化(StandardScaler)
训练集中某一列数值特征(假设是第i列)的值缩放成均值为0,方差为1的状态。标准化之后,数据的范围并不一定是0-1之间,数据不一定是标准正态分布,因为标准化之后数据的分布并不会改变,如果数据本身是正态分布,那进行标准化之后就是标准正态分布。
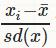
综上:在PCA,聚类,逻辑回归,支持向量机,神经网络这些算法中,StandardScaler往往是最好的选择,
1、归一化和标准化的相同点都是对某个特征(column)进行缩放(scaling)而不是对某个样本的特征向量(row)进行缩放。对行进行缩放是毫无意义的。比如三列特征:身高、体重、血压。每一条样本(row)就是三个这样的值,对这个row无论是进行标准化还是归一化都是无意义的,因为你不能将身高、体重和血压混到一起去。
2、标准化/归一化的好处
- 提升模型精度:基于距离的算法,例如Kmeans、KNN等,各个特征的量纲直接决定了模型的预测结果。举一个简单的例子,在KNN中,我们需要计算待分类点与所有实例点的距离。假设每个实例点(instance)由n个features构成。如果我们选用的距离度量为欧式距离,如果数据预先没有经过归一化,那么那些绝对值大的features在欧式距离计算的时候起了决定性作用。对于PCA,如果没有对数据进行标准化,部分特征的所占的信息可能会虚高。
- 提升收敛速度:例如,对于线性model来说,数据归一化后,最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。对于SVM标准化之后梯度下降的速度加快。
3、标准化/归一化的对比分析
首先明确,在机器学习中,标准化是更常用的手段。
- MinMaxScaler对异常值非常敏感。例如,比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。在PCA,聚类,逻辑回归,支持向量机,神经网络这些算法中,StandardScaler往往是最好的选择。
- 当数据需要被压缩至一个固定的区间时,我们使用MinMaxScaler.
4、在逻辑回归中需要使用标准化么?
- 如果你不用正则,那么,标准化并不是必须的,如果你用正则,那么标准化是必须的。为什么呢?因为不用正则时,我们的损失函数只是仅仅在度量预测与真实的差距,加上正则后,我们的损失函数除了要度量上面的差距外,还要度量参数值是否足够小。而参数值的大小程度或者说大小的级别是与特征的数值范围相关的。
- 举一例来说,我们预测身高,体重用kg衡量时,训练出的模型是: 身高 = x*体重+y*父母身高,X是我们训练出来的参数。当我们的体重用吨来衡量时,x的值就会扩大为原来的1000倍。在上面两种情况下,都用L1正则的话,显然当使用kg作为单位时,显然对模型的训练影响是不同的。
- 再举一例来说,假如不同的特征的数值范围不一样,有的是0到0.1,有的是100到10000,那么,每个特征对应的参数大小级别也会不一样,在L1正则时,我们是简单将参数的绝对值相加,因为它们的大小级别不一样,就会导致L1会对那些级别比较大的参数正则化程度高,那些小的参数都被忽略了。
- 就算不做正则化处理,建模前先对数据进行标准化处理也是有好处的。进行标准化后,我们得出的参数值的大小可以反应出不同特征对label的贡献度,使参数具有可解释性。
5、有些需要保持数据的原始量纲的情况下,不能对数据进行标准化或者归一化处理。例如,制作评分卡
正则化
这篇文章对于正则化的讲解通俗易懂:https://www.zhihu.com/question/20924039
正则化主要用于防止过拟合
我们在训练模型时,要最小化损失函数,这样很有可能出现过拟合的问题(参数过多,模型过于复杂),所以我么在损失函数后面加上正则化约束项,转而求约束函数和正则化项之和的最小值。
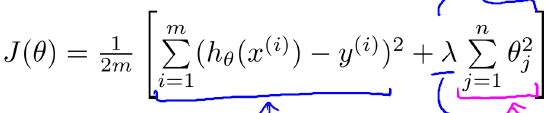
上式中,蓝色部分即为损失函数,红色部分是正则化项(参数的2-范数)