Houdini中全景摄像机shader立体左右眼成像方法

熟悉Houdini Shader部分的同学应该多多少少也了解camera自身也可以设定自己的shader。其中polar panoramic shader 能够非常方便的为艺术家渲染360全景视角的cg画面，但是这样渲染出来的画面只是单眼所看到的环境，如果引入立体双摄像机的渲染方法的话，默认的这个摄像机shader就会出现一个严重的问题，那就是所渲染出来的画面是分别以各自两台摄像机位置为原点所计算出来的。用文字说明可能有点绕口，看下图：

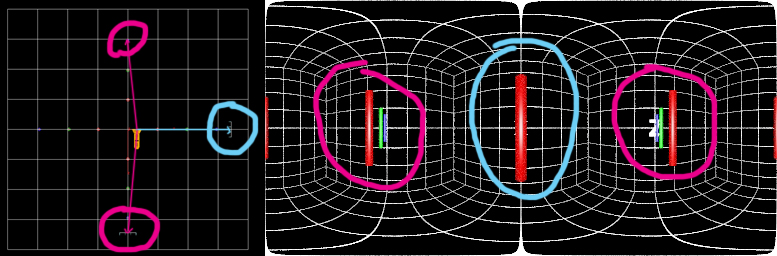
图片中我把摄像头在一个水平轴向上移动了一点，渲染出来的结果发现垂直方向上粉红圈圈确实是因为一定的位移看到了柱子后面的东西，但是前后是反的，而且最要命的是水平方向上还是被挡着的，主要原因就是因为渲染的采样原点是摄像机自身中心点。这和我们实际旋转头部得到的影像是不一样的。生活中如果要看我们左边的事物，绝对不是两眼珠子自己左转九十度而是由我们的头部旋转来帮助眼睛看到目标。所以这种情况下实际上的两只眼睛对身边环境的成像是共享了同一个旋转中心点，且中心点绝不会在任意眼珠上。

如下图模型，O点才可能成为polar panoramic shader的旋转点，而射线投射点的位置待会再细聊：

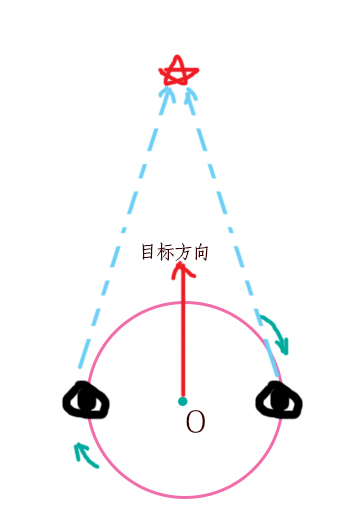
确定好正确的摄像机渲染原型之后就是怎样把这个方法放入到Houdini的摄像机上，好在Hou很灵活的提供了camera自身的shader入口，而且shop下面的ASAD Lens节点给我们提供了一个非常好的shader模板，里面含有perspective/polar pano/ cylinder pano 的shader方法。打开节点的script能够拿到当前polar全景的摄像机方法：

..................
 else if (projection == "polar")
    {
        float   xa = -PI*x;
        float   ya = (0.5*PI)*y;
        float   sx = sin(xa);
        float   cx = cos(xa);
        float   sy = sin(ya);
        float   cy = cos(ya);

        P = 0;
        I = set(cx*cy, sy, sx*cy);
    }
...................

短短几行，但是包含的内容实在太多了，我这里分别介绍一下不做太多扩展：

1：Houdini中camera shader的入口和出口

写shader的都知道一定会有入口和出口的定义，摄像机shader也不例外。其中入口参数有x,y,Time 等等， 输出端的参数则是P, I。具体对应什么摄像机的帮助文档写的比较详细了，这里截下来比较关键的定义:

//float x – X screen coordinate in the range -1 to 1
//
//float y – Y screen coordinate in the range -1 to 1
//
//float Time – Sample time
//
//float dofx – X depth of field sample value
//
//float dofy – Y depth of field sample value
//
//float aspect – Image aspect ratio (x/y)
//
//export vector P – Ray origin in camera space
//
//export vector I – Ray direction in camera space
//
//export int valid – Whether the sample is valid for measuring

理解起来也不会太难，x,y都是摄像机横轴纵轴的采样点，是[-1,1]空间里给像素点定义的坐标系，P 设摄像机发射出射线的起始点位置，I 则是射线方向。

这里涉及到的问题就在 P = 0; 上。

2：球形坐标系(Spherical coordinates)与笛卡尔坐标系(Cartesian coordinates)之间的关系：

笛卡尔坐标系大家都熟悉，就是(x,y,z)三个轴向的数据确定空间的一个点。而球形坐标的参数则有点不一样，我们拿地球做比，地球有经度与纬度，两个度数就能确定地球球面的任何一个位置，准确来讲是要加上地球半径才真的定位到了球面上，只不过我们已经在球面上了也不会混淆说成地底下所以从来不会去碰地球半径这个参数了。其实这就是球形坐标系的原型，纬度跨度有2π，经度跨度则是一个π。如下图：

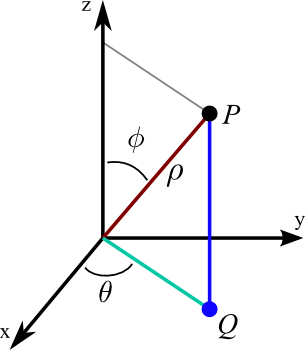
θ是纬度，φ是精度，ρ则是到原点的距离，由这三个数值我们就能建立球形坐标系在在笛卡尔坐标系中的表达了,另外考虑到houdini的摄像机空间是横轴纵轴都是[-1,1]。所以可以得到上面代码中的公式了：

x = cos(xa) * cos(ya)

y = sin(ya)

z = sin(xa) * cos(ya)

这些内容是为了理解摄像机的平面坐标到球形空间坐标的一个变换关系。如果还是觉得难以理解我把上面的方法直接通过vop运用到了一个grid上的每一个点上来观察。其中grid是在xy平面上大小为2的正方形面板，反正我们这里先不考虑画幅高宽的ratio。

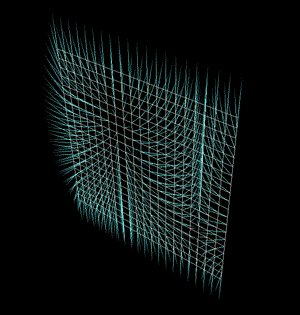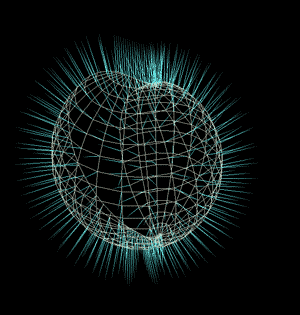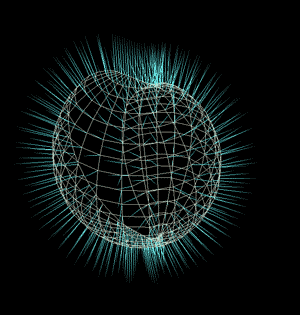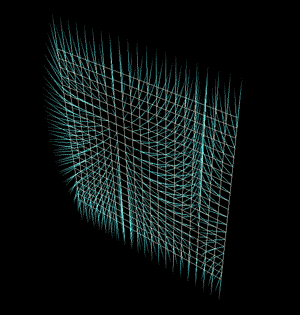
grid上面的每一个点可以看成屏幕或者摄像机的每一个像素点，整个屏幕每个点投射出去的射线正好能组成一个圆球的所有方向，这就是polar panorama的奥秘了。

回到上面留下来的问题 P = 0, 这个等式直接就把射线的投射点固定在了一个位置上，所以我们只要改变它，使它随着射线方向的变化而变化“位置”。

如图，假如我们设定一个投射方向k：

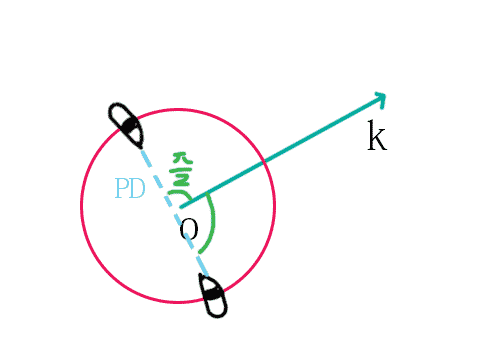
那么两只眼睛的连线必与射线k垂直，而PD则定义了我们人的瞳距。射线k我们知道那么正向和反向旋转90度则能求出两只眼睛在xz平面上的方向，最后乘以瞳距的一半便能求出眼睛在当前射线上的具体位置。

废话了这么多基本上就是houdini 360全景双眼渲染的方法了。再贴一下我在cvex里面实现的这个方法：

//float x – X screen coordinate in the range -1 to 1
//
//float y – Y screen coordinate in the range -1 to 1
//
//float Time – Sample time
//
//float dofx – X depth of field sample value
//
//float dofy – Y depth of field sample value
//
//float aspect – Image aspect ratio (x/y)
//
//export vector P – Ray origin in camera space
//
//export vector I – Ray direction in camera space
//
//export int valid – Whether the sample is valid for measuring

#pragma hint    x       hidden
#pragma hint    y       hidden
#pragma hint    Time    hidden
#pragma hint    dofx    hidden
#pragma hint    dofy    hidden
#pragma hint    aspect  hidden
#pragma hint    P       hidden
#pragma hint    I       hidden

#pragma hint    side    oplist
#pragma choice  side    0 "right"
#pragma choice  side    1 "left"

#pragma label   offest  "Pupil Distance"

#include "math.h"

cvex
paronamaLens(
            // Inputs
            float x = 0;
            float y = 0;
            float Time = 0;
            float dofx = 0;
            float dofy = 0;
            float aspect = 1;
            float offest = 1;
            int side = 0;
      
            // Outputs
            export vector P = 0;
            export vector I = 0;
            )
{
   float   halfPI = 0.5 * PI;
   float   xa = -PI * x;
   float   ya = halfPI * y;
   float   sx = sin(xa);
   float   cx = cos(xa);
   float   sy = sin(ya);
   float   cy = cos(ya);

   //correspondent position for eyes
   float px, pz, rotation;
   rotation = lerp(-halfPI, halfPI, side);

   px = cos(xa + rotation) * cos(ya);
   pz = sin(xa + rotation) * cos(ya);

   P = 0.5 * offest * set(px, 0 , pz);
   I = set(cx*cy, sy, sx*cy);
}

 最后我把视距拉大一点看看极端效果：

左眼：

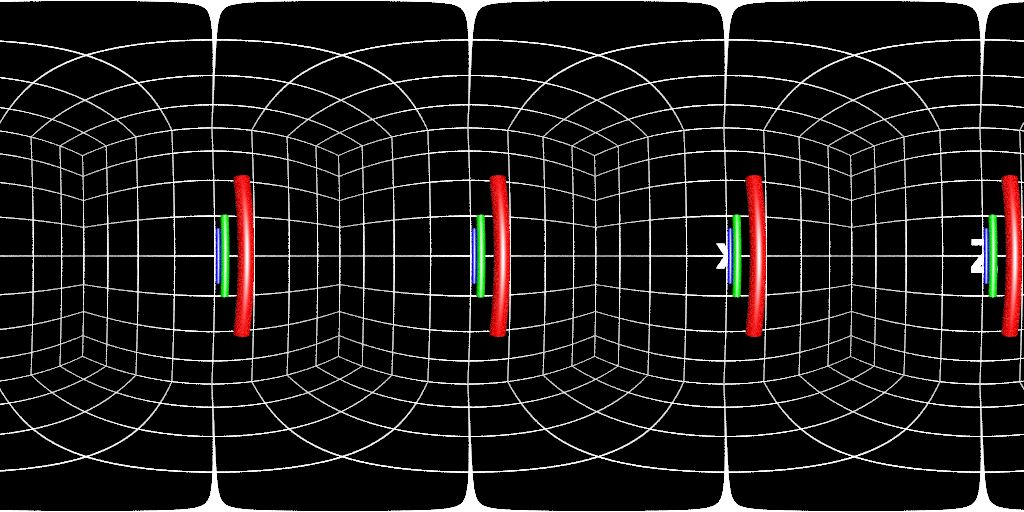
右眼：

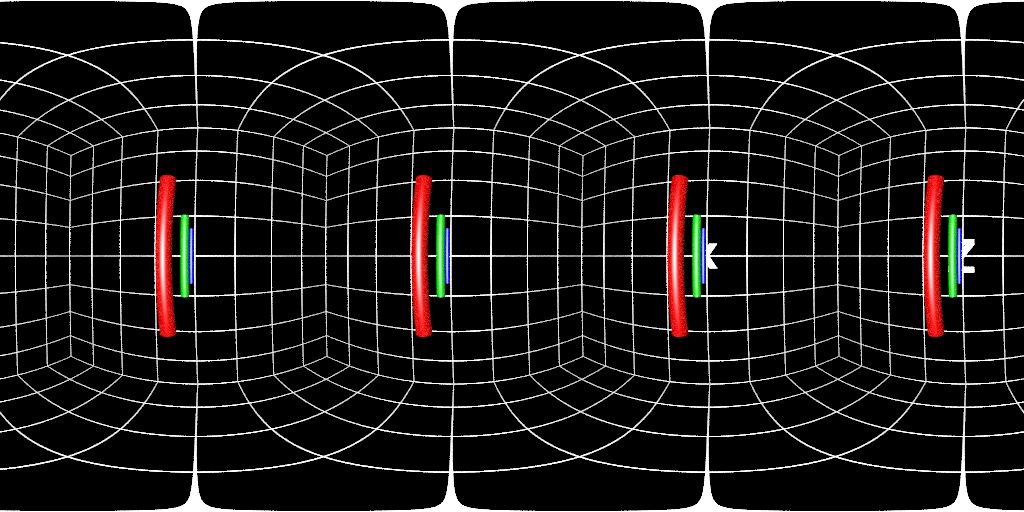
很好，四个方向都是真确的偏移。打完收工。