Houdini 中Volume Retiming 放慢速度的方法

阅读这篇博客读者可能需要对体积的概念掌握程度比较高，如果因概念不太熟悉而造成阅读中身体不适的，还请回头自行补课。

设计这个解决方案的原因主要是有些镜头中的烟火效果可能形态很好但就是觉得速度需要放慢点。而恰恰Houdini自带的retiming方法做插值的话是会出现类似鬼影的问题，常常结果是不能用的。昨天通过挪威同事指点后，自己也做了一个方案，这里讲讲我的思路。

首先是效果：

 

从图中可以看出，虽然用这个方法仍然不能避免抖动的存在，但是整体过渡确实缓和流畅多了，传统方法效果是整个烟雾不论速度快的还是慢的都会出现一定程度的抖动，而改进后的方法抖动的地方都是速度过快导致误差增大而产生的。所以如果烟效的速度在一定程度的话，或者density比较厚而不太透明的话，这个插值方法是能比较准确表达出过渡的。

如下图，我们假定当前要计算的voxel是P，我们需要计算这个voxel里面density的值从n到n+1的过渡，假设我们的substep设置成0.1，那么相当于放慢了十倍，中间需要插九帧。

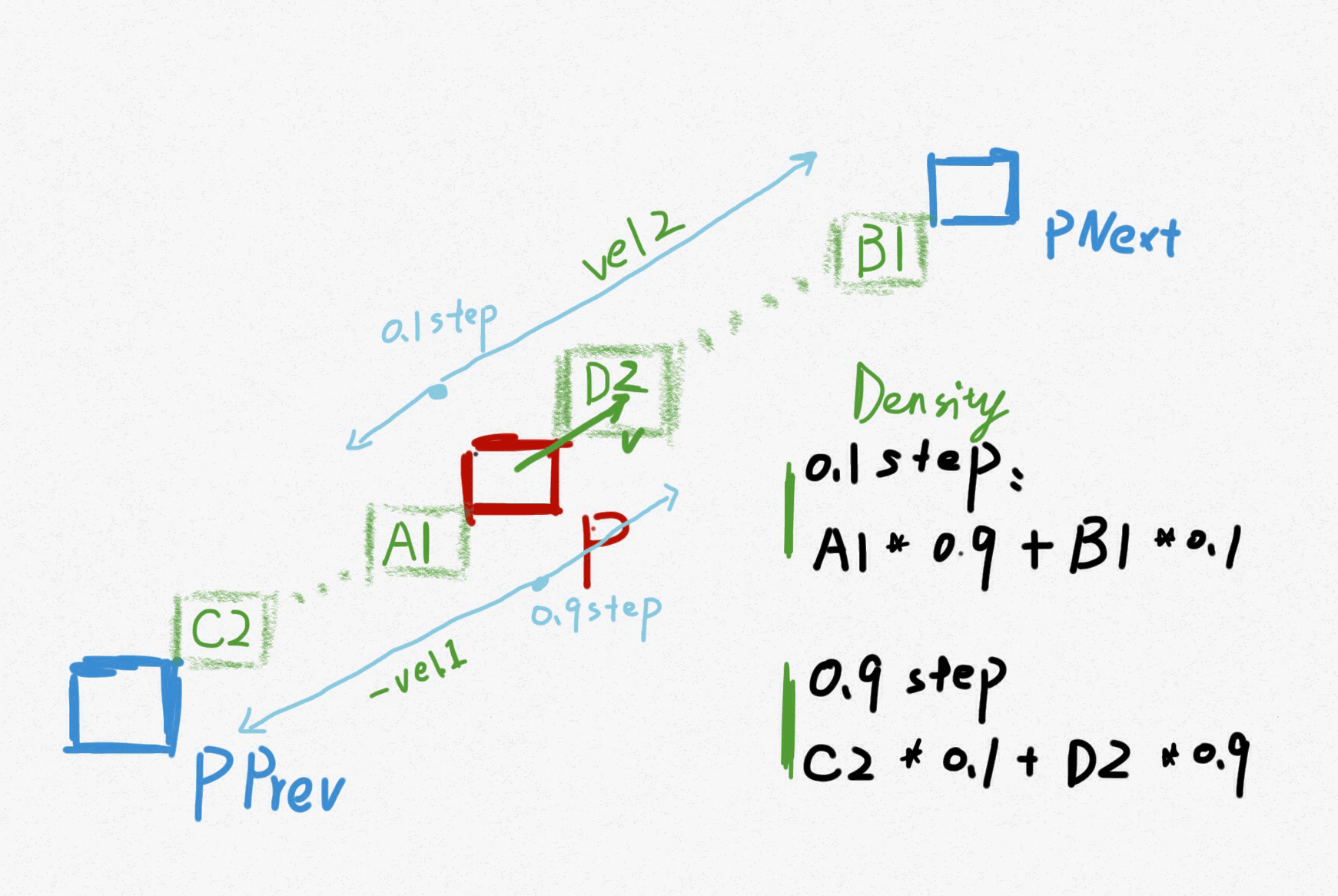
我们先考虑第一个substep的情况，也就是第一个0.1的情况。因为是从n到n+1的帧的过渡，所以当前帧的基础帧我们会用到第n帧，采样出他的速度为vel1，通过速度乘以TimeInc和substep之后的向量尺度则相当为一个substep的跨度（这里我们只能假设帧与帧之间是线性变化的，即便肯定不是线性的）。虽然vel1在理解上肯定是向前的，但在计算voxel的时候我们一直是在讨论一个固定点上采样他的某个值，这里是density，所以我们不能用sop vop里的常用思维来思考物理位置的变化。我们先考虑n.1步的时候点P的density值最有可能是哪些位置的density转移过来的，我们只能从两帧中来做评断，在n帧里面我们把vel1计算出的向量向后推一步得到A1。在判定n+1帧里面哪个位置的density最可能组成n.1的density前，我们先需要得到次P点在n+1帧的速度，假设为Vel2。根据这个速度我们可以猜出（只能是猜）n帧在点P的density很可能在n+1帧中在点PNext的位置，所以n.1的density在n+1帧中很可能就在B1的位置。同理，在n.9步中最可靠的值在n帧的C2和n+1帧的D2中。是不是很绕啊，没办法就通过一个速度来判定一个固定地方某个值的前世今生确实比较耗脑力。

在如何混合A1和B1这两个density的问题上，我们还得清楚以点P为参考的计算，越是离点P近的点的值越是准确，因为速度越大，跨度就越大，这样density在速度的积累下就越散，所以就越不精确。所以在计算n.1步时，如果是使用线性混合的方法的话，那么比较准确的方式为density = A1*0.9+B1*0.1。同理在n.9步中density = C2*0.1 + D2*0.9。

到目前为止我们的插值模型就算完成了，接着就是怎么实现的了，我简单截一下用volume vop连的方法和直接用Vex写的方法两种，大同小异，计算时间也相差不大。

在链接volume vop之前需要得到timeshift之后的n帧和n+1帧，链接如下：

 

在volume vop里面的链接为：

 

这是Vex的方法，是通过vop的连接为原型直接转译写出来的，没什么太多好讲的。

float subProcess = ch("subProcess");

float currentVelX, currentVelY, currentVelZ;
float nextVelX, nextVelY,nextVelZ;

int curAttribValueX, curAttribValueY, curAttribValueZ;
int nextAttribValueX, nextAttribValueY, nextAttribValueZ;

//find the primitive index for each input
//find the right way to get the velocity values
curAttribValueX = findattribval( @OpInput1, "primitive", "name", "vel.x");
curAttribValueY = findattribval( @OpInput1, "primitive", "name", "vel.y");
curAttribValueZ = findattribval( @OpInput1, "primitive", "name", "vel.z");

nextAttribValueX = findattribval( @OpInput2, "primitive", "name", "vel.x");
nextAttribValueY = findattribval( @OpInput2, "primitive", "name", "vel.y");
nextAttribValueZ = findattribval( @OpInput2, "primitive", "name", "vel.z");

//get the velocity of frame n
currentVelX = volumesample(@OpInput1, curAttribValueX, @P);
currentVelY = volumesample(@OpInput1, curAttribValueY, @P);
currentVelZ = volumesample(@OpInput1, curAttribValueZ, @P);
vector currentVel = set(currentVelX, currentVelY, currentVelZ);

//get the velocity of n+1 frame
nextVelX = volumesample(@OpInput2, nextAttribValueX, @P);
nextVelY = volumesample(@OpInput2, nextAttribValueY, @P);
nextVelZ = volumesample(@OpInput2, nextAttribValueZ, @P);
vector nextVel = set(nextVelX, nextVelY, nextVelZ);

//get the density sample position from frame n
vector forbackCurrentDirection, currentCheckPos;
forbackCurrentDirection = -1 * currentVel * @TimeInc * subProcess;
currentCheckPos = @P + forbackCurrentDirection;

//get the density sample position from frame n+1
vector forwardNextDirection, nextCheckPos;
forwardNextDirection = nextVel * @TimeInc * (1 - subProcess);
nextCheckPos = @P + forwardNextDirection;

//sample the density
float forbackCurrentDensity, forwardNextDensity;
int curAttribValueDensity, nextAttribValueDensity;
curAttribValueDensity  = findattribval( @OpInput1, "primitive", "name", "density");
nextAttribValueDensity = findattribval( @OpInput2, "primitive", "name", "density");

forbackCurrentDensity = volumesample(@OpInput1, curAttribValueDensity, currentCheckPos);
forwardNextDensity = volumesample(@OpInput2, nextAttribValueDensity, nextCheckPos);

//mix the density by the distance from the current sample position
float finalDensity;
finalDensity = subProcess * forbackCurrentDensity + (1 - subProcess) * forwardNextDensity;
@density = finalDensity;