图像分割是由图像处理进到图像分析的关键步骤。它是目标表达的基础,使得更高层的图像分析和理解成为可能。
基本依据:
1.区域内的一致性
2.区域间的不一致性
基本方法:
1.基于区域的方法
2.基于边缘的方法
3.综合考虑边缘和区域信息的混合分割方法
***4.基于特定理论的方法(重点讲解)
基于区域的方法
I.阈值法
有针对双峰单谷直方图的取法,也有迭代均值法。
优点:算法时间复杂度较低,易于实现,适合应用于在线实时图像处理系统。
不足:忽略了图像的空间位置信息
还有局部阈值法和多阈值法。
II.区域生长法
先以高阈值选取确信度较高的种子区域,从种子区域开始以8邻域方式增长,像素灰度与种子灰度相差小于一个数值(认为给定)就进行生长,即选为目标区域。
III.分水岭分割法
标准步骤:
1)将图像看作地形图;(在三维中,长宽为图像的长宽,高度为相应的灰度值)
2)在每一个极小点处"打一个孔";(这里的极小点可以用梯度获取,也可以人工对兴趣点标记)
3)以一致的速率从小孔向外"喷水",并始终保持地形中所有的水位一致;(所谓高度是指灰度值逐渐上升)
4)不同盆地的水相遇时则筑坝,并且随着水位的不断升高,坝也升高;(这个坝所在的位置最后就成了分割的边界)
5)当水位达到地形的最高点时算法终止
注:通过手工标注的方式给出打孔点可以有效防止过度分割,另外一个防止过度分割的方法是滤波。
基于边缘的方法:略
基于特定理论的方法
1.均值移动,mean-shift,也叫均值漂移
核心思想:找到概率密度梯度为零的采样点,并以此作为特征空间聚类的模式点。
首先解决的问题如何进行概率密度估计,思想来源于非参数概率密度估计中的Parzen窗。
用一个核函数来加权该点周围固定体积内的点对该点概率密度值的贡献,

这里使用众多核函数中的一种,如下形式

对估计出来的概率密度函数求梯度,希望找到梯度为零的采样点作为模式点




在这里我们把概率密度的梯度表示成了一个核函数和一个均值漂移向量的乘积形式。
接下来就是要反复的计算m(x)向量,来移动核窗G(x)。直到m(x)的幅值小于一个给定的值时 ,我们认为那个概率密度梯度为零的点已经找到。
注:他与梯度下降(上升)的方法很相似,但是又有自己的优势,就是每次迭代的步长是由x的位置确定的 ,有人也管他叫自适应梯度上升算法。
Mean-shift 本质上是一个优化局部最值的方法,应用在图像分割中的具体做法:
a.特征提取(位置,灰度,彩色信息等);
b.set kernel size for features Kf and position Ks;
c.initialize windows at individual pixel locations;
d.perform mean shift for each window until convergence;
e.merge windows that are within width of Kf and Ks.
这里的推导只是示意性的,详情请参考:http://pan.baidu.com/s/1pLzOECV
在http://blog.csdn.net/carson2005/article/details/7337432中也有通俗的说法。
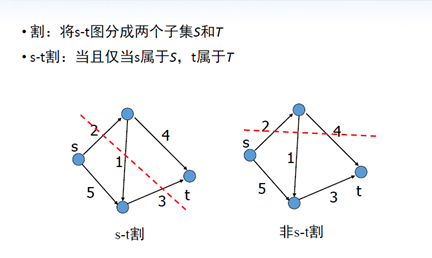
2.Graph cut(图割)
•基本思想:
• 1. 将图像用图的方式表示,顶点表示像素,边表示像素之间的关系。图像分割对应图的割集。
• 2. 确定图中边的权值,使图像分割目标(能量最小化)对应图的最小割。
• 3. 用最大流算法求解最小割问题。
图论中的相关基础知识



2.1 Ncut
参考:Jianbo Shi, Jitendra Malik, Normalized cuts and image segmentation[J]. IEEE Trans on PAMI, 2000; 22(8): 888-905.
链接:http://pan.baidu.com/s/1kVjbQZ1
思想来源是:当我们把一幅图像表示成图链接的形式时,对于二分问题

w是权重矩阵,通常定义为:

其中 F是像素值,X是距离值。
我们的目标是让其取得最小值,也就是类间相似度最小。
我们可以用寻求最小割的方法来得到一幅图像的分割,但在实际应用中却出现了很多孤立像素点的分割,这并不是我们想要的。
这篇文章中就提出了一种解决这个问题的方法:
类间相似性度量
 ,其中
,其中
类内相似度度量

可以证明最小化类间相似性与最大化类内相似性是等价的。
那么问题来了,如何最小化Ncut(A,B)
文章中给出了一种利用广义特征值的方法得到问题的近似解。
做法是,先将链接相似度矩阵w的行求和得到wi,令矩阵D=dig{wi};
然后求

求得其次小的特征值所对应的特征向量,将特征向量通过阈值(0或者中点)进行离散化就能够得到分割结果。
2.2针对多标记问题的能量极小化模型

这里的f表示了一种标记,即从数据点集P到标记集合L的映射。
data项是表示由这种标记带来的直接代价。smooth项是说如果这样标记了,相邻像素之间的约束代价。
用图形表示如下(这里只是表示两个标签):

问题就变成了求解一个标签集合使得能量函数E最小化。
求解两类标签,和多类标签的能量极小化问题在数学中都有对应的算法
参见:Yuri Boykov, Olga Veksler, and Ramin Zabih. Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(11):1222–1239, November 2001.
链接:http://pan.baidu.com/s/1c1AKmRI