概率密度函数估计是贝叶斯决策的基础,有两大类方法:参数法和非参数法。所谓的参数法是指已知参数形式,但不知道参数,我们要对参数进行估计的过程。这里主要介绍点估计的两种方法:一种是最大似然估计,一种是贝叶斯估计。
最大似然估计
假设:
- 我们要估计的参数
 是确定但未知的;
是确定但未知的;
- 样本之间是独立同分布的(或者是条件独立,即在某一个固定的条件下样本是独立的);
- 类条件概率密度的分布形式已知;
- 不同类别之间的参数是独立的。
主要步骤:
- 求似然函数:
 ;
;
- 最大化似然函数 :
 。
。
注: ,成立的原因是假设条件2,即样本之间独立同分布。
,成立的原因是假设条件2,即样本之间独立同分布。
在具体的求解过程中通常转换为对数似然: ,然后求
,然后求  。
。
转换为对数似然有两点好处:
- 由乘法运算转换为加法运算;
- 对数似然能对
 的有效域进行拓宽见下图。
的有效域进行拓宽见下图。

举例 :高斯分布参数的似然估计
这里讨论方差已知,估计均值的情况
对数似然函数 ,其中
,其中
上式对 求导得
求导得 ,其中用到公式
,其中用到公式 。
。
求和得 ,解得
,解得 
参数估计第二种,贝叶斯估计
将参数 看成一个服从某种分布的随机变量,通过对其后验的求取来估计样本变量的概率密度
看成一个服从某种分布的随机变量,通过对其后验的求取来估计样本变量的概率密度
公式如下: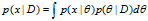 ,其中
,其中 ,即
,即  的后验=似然*先验/归一化因子 。
的后验=似然*先验/归一化因子 。
注:这里估计得到的是一个分布的密度函数,并不是一个数,这是和似然估计的表观区别。
举例:高斯分布的贝叶斯估计
同样讨论方差已知,估计均值
先验分布:采用高斯分布
似然:
后验: 
将高斯分布的函数代入得到
 的期望
的期望

其中 ,即为似然估计中的估计值。
,即为似然估计中的估计值。
注:对以上两种方法估计的结果进行比较得,当贝叶斯估计的样本个数n趋于无穷时,贝叶斯估计得到的分布的期望值会接近于最大似然估计得到的估计结果;当贝叶斯估计中的n接近于零的时候,其估计得到的分布与先验分布接近。