第二次DS博客作业
Q0.展示PTA总分

Q1.本章学习总结
1.1 学习内容总结
- 栈
-
什么是栈?
同有序表、链表一样,栈也是用来存储逻辑关系为 "一对一" 数据的线性存储结构。但是栈的存储结构与它们不同,无论是存数据还是取数据,遵循“先进后出”的原则,即最先进栈的元素最后出栈(Last In First Out)。一个简单的例子,向一个栈中依次放入1、2、3,再进行出栈,则会得到结果3、2、1。
总结来看,栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。 栈分为顺序栈和链栈,即分别为数组、链表实现栈。
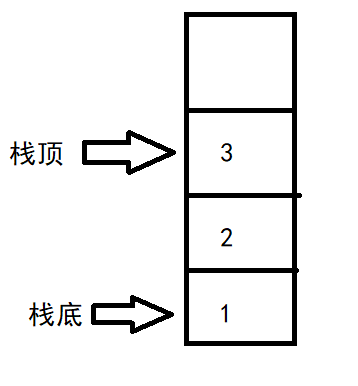
对于栈,为了方便理解,我们可以将它看作是一个“桶”,我们要向桶里拿东西、放东西,都只能放在桶的顶部,也就是栈顶,而不能直接拿、放中间的某个部分。
例如下图,我们要取元素只能取到栈顶的3,而不能直接拿到1或者2;要存元素,我们只能将其放在3的上面,而不能塞到2与3中间。
-
栈的定义与初始化
这里分别给出一个顺序栈和链栈的定义,后文的举例会用到它们。
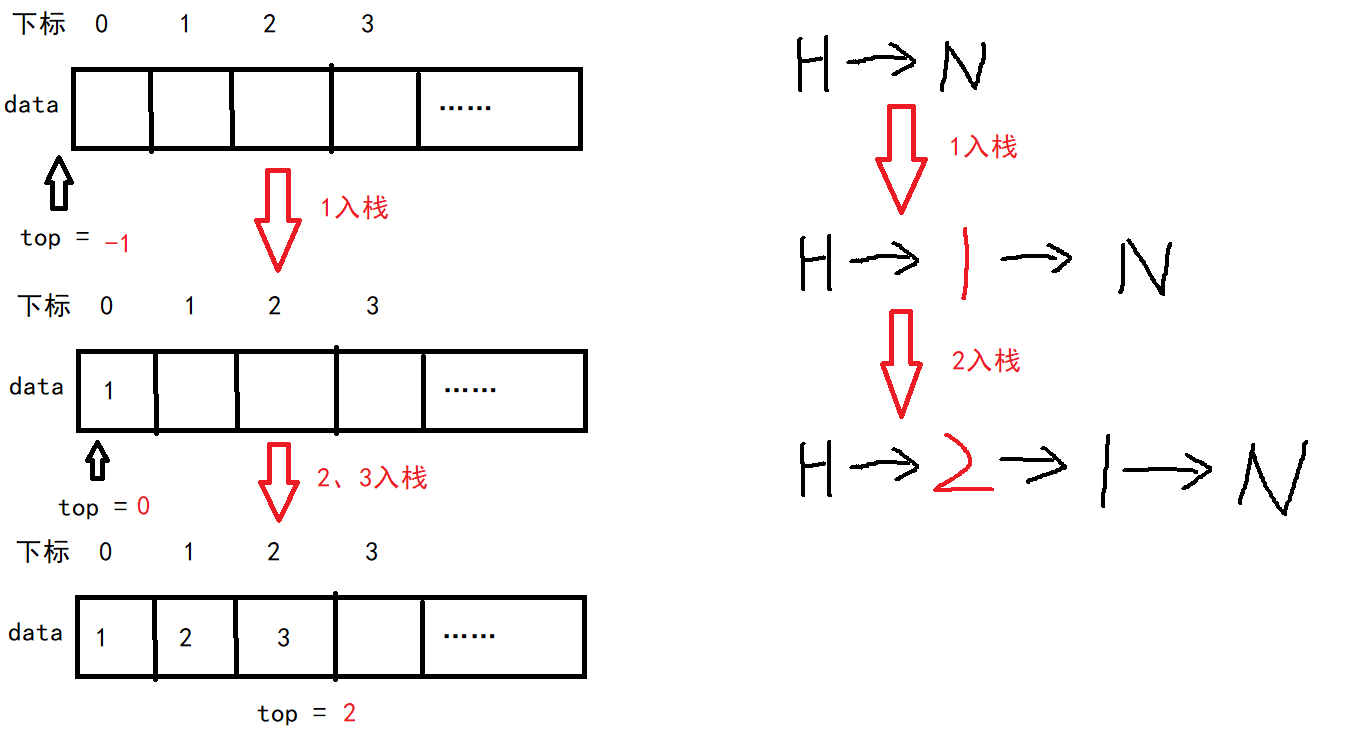
顺序栈的初始化,只需定义top的值为-1,代表栈为空
链栈初始化只需新建一个空链表,设置头结点next结点为空即可,我们采用带头结点的单链表
-
typedef struct SeStack //顺序栈
{
int data[MaxSize]; //MaxSize代表栈的元素最大数量
int top; //指向栈顶
};
typedef struct LiStack //链栈
{
int data; //链栈则不用担心栈的大小了
struct LiStack* next; //后继节点指针
};
- 判断栈是否为空
在上文初始化的基础上,我们很容易就能推出栈空的条件
顺序栈的栈空条件即为top的值为-1,链栈的栈空条件为头结点的next结点为空(使用带头结点的链表)
bool StackEmpty1(SeStack* S) //判断顺序栈是否为空,为空返回true,不空返回false
{
if (S->top == -1) //顺序栈为空的条件
return true;
return false;
}
bool StackEmpty2(LiStack* S) //判断链栈是否为空,为空返回true,不空返回false
{
if (S->next == NULL) //链栈为空的条件
return true;
return false;
}
- 入栈
对于顺序栈,在入栈前我们要先判断栈是否已满,即top是否等于maxsize-1(因为我们的top从-1开始),然后再进行入栈,并且要让top值+1
而链栈就不用考虑栈满的情况,我们直接采用头插法来实现入栈操作,这样方便我们出栈等操作
bool Push1(SeStack *S, int x) //顺序栈入栈元素x
{
if (S->top == MaxSize - 1) //栈满
{
return false;
}
//注意要先修改栈顶元素的下标,再进行赋值
S->top++;
S->data[S->top] = x;
return true;
}
bool Push2(LiStack &S, int x) //链栈入栈
{
LiStack *temp = new LiStack;
temp->data = x;
temp->next = S->next;
S->next = temp; //就是链表的头插法
return true;
}
- 出栈
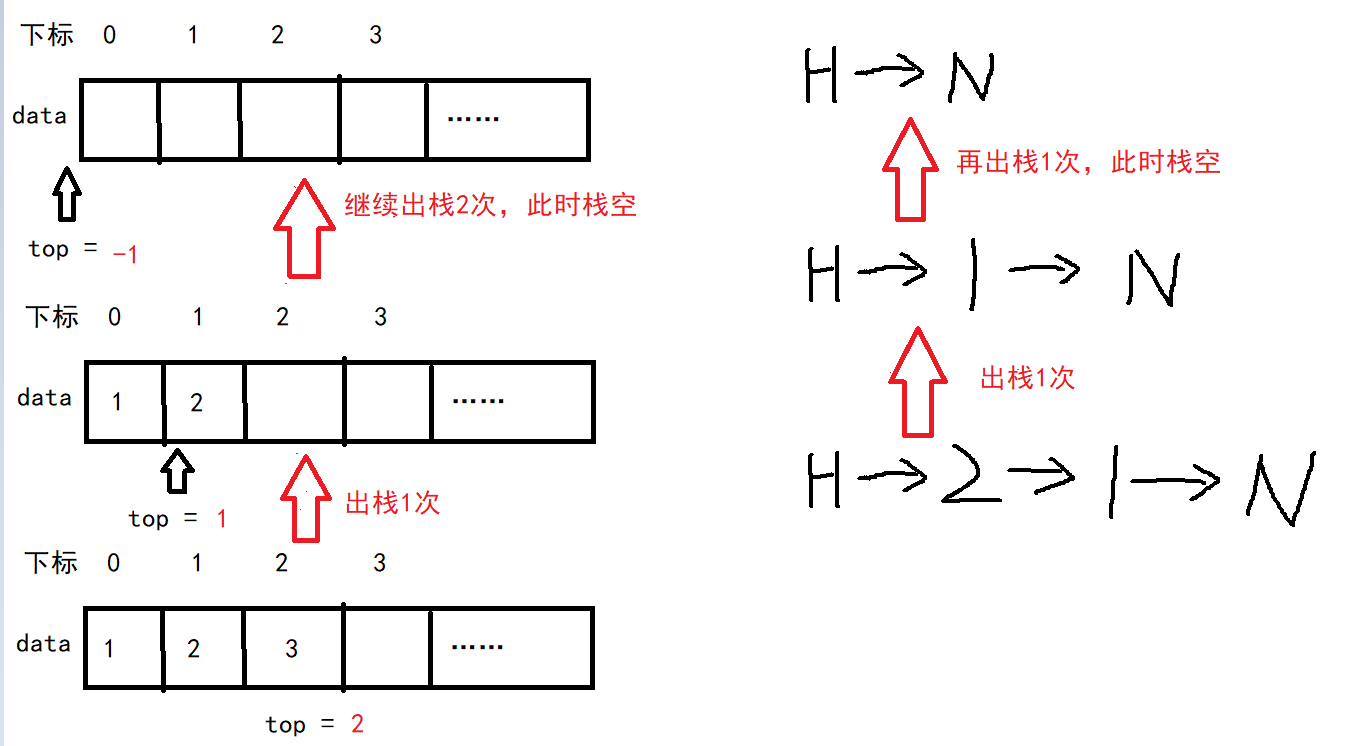
不论是顺序栈还是链栈,在出栈前都要先判断栈是否为空!
不能忘记顺序栈要在出栈后将top的值-1,链栈的出栈要释放内存空间
bool Pop1(SeStack *S, int &e) //删除栈顶元素,并将原栈顶的值给e
{
if(EmptyStack1(S) == true) //栈空,不能出栈
{
return false;
}
e = S->data[S->top]; //记录栈顶的值
S->top--; //top值减1
return true;
}
bool Pop2(LiStack &S, int &e) //链栈的情况
{
LiStack *temp = new LiStack;
if(EmptyStack2(S) == true) //栈空,不能出栈
{
return false;
}
temp = S->next; //相当于删除链表头结点的后一个结点
e = temp->data; //记录被删除的栈顶的值
S->next = temp->next;
delete temp;
return true;
}
-
关于stack库
- c++中的stack库可以有效、简易的帮我们做成一个栈,以下是他的一些函数
- 定义: stack<栈中数据类型>栈的名字;
- size():返回栈中元素个数
- top():返回栈顶的元素
- pop():删除栈顶元素
- push(e):向栈中添加元素e
- empty():栈为空时返回true(等同于栈的size()==0)
-
栈的应用
- 符号的配对:我们在使用VS编写程序时,当左右括号((、[、{、/*)不匹配时就会跳出错误提示,我们可以利用栈来模仿实现这一功能
- 简单思路如下:有序读入一段字符串,遇到左括号则将它们入栈,遇到右括号则判断栈是否为空且栈顶元素是否匹配,两者条件有一不符合即不配对,且在读完所有字符后,还要判断栈中是否还有元素剩余,若有剩余也是不匹配
- 中缀表达式转后缀表达式
- 主要有几点需要注意:
- 1.根据运算符的优先级考虑进栈和出栈,特别注意右括号,它会进行出栈操作直到遇到左括号(并将其左括号也出栈)
- 2.小数:伴着数字,只需要一起输出就可以
- 3.正负号:也有分情况,第一个情况,数是正负数时是没有括号的(如-3+1),第二种情况,算式中间的正负数(如(-1)、(+3)),且注意正数不需要输出正号
- 4.有可能算式遍历完,栈中还有剩余符号,也要输出出来
- 下面以2+3*(7-4)+8/4作为例子讲解
- 1.直接输出2,因为栈空,加号直接入栈,此时栈中元素为 + ,输出结果为2
- 2.输出3,乘号优先级大于栈顶的加号,所以入栈,左括号优先级大于栈顶的乘号,也入栈,此时栈中元素为 + * ( ,输出结果为2 3
- 3.输出7,遇到减号,虽然优先级低于左括号,但因为此时栈顶即为左括号,所以入栈,此时栈种元素为 + * ( - ,输出结果为2 3 7
- 4.输出4,此时遇到右括号,出栈直到栈顶为左括号,并出栈左括号,此时栈中元素为 + * ,输出结果为2 3 7 4 -
- 5.遇到加号,此时栈顶为乘号,优先级高于加号,则出栈乘号,接下来栈顶为加号,优先级相等,出栈加号后自己入栈,此时栈中元素为 + ,输出结果为2 3 7 4 - * +
- 6.输出8,遇到除号,除号优先级高于栈顶的加号,所以直接进栈,此时栈中元素为 + / ,输出结果为2 3 7 4 - * + 8
- 7.输出4,字符串已全部读完,栈中还有元素剩余,将它们全部出栈,得到最终结果2 3 7 4 - * + 8 4 / +
- 下面给出伪代码思路
- 主要有几点需要注意:
- 符号的配对:我们在使用VS编写程序时,当左右括号((、[、{、/*)不匹配时就会跳出错误提示,我们可以利用栈来模仿实现这一功能
初始化一个map,例如加减号为1,乘除为2,左括号为3
While 遍历字符串s do
if 运算数是正负数(s[0]即为+ -或左括号后即为+ -号) then
直接输出符号(+号不输出)和后面的数字,左右括号忽略跳过
End if
If s[i]为数字或.号 then
输出数字或点号直到s[i]不是数字
End if
If s[i]为运算符 then
If 栈为空或栈顶为左括号 then
S[i]入栈
Else if s[i]不为右括号 then
输出栈顶符号并出栈直到栈空栈顶符号优先级小于s[i]或栈顶为左括号
S[i]入栈
Else if s[i]为右括号 then
输出栈顶符号并出栈直到栈顶为左括号,并出栈左括号
End if
End while
如果循环结束后栈不空,依次输出栈中剩余元素
- 队列
- 什么是队列?
队列和栈一样,也是一种对数据的"存"和"取"有严格要求的线性存储结构。
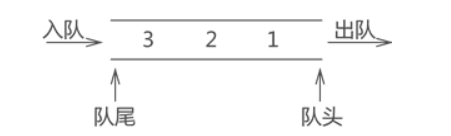
与栈结构不同的是,队列的两端都"开口",要求数据只能从一端进,从另一端出。通常称进数据的一端为 "队尾",出数据的一端为 "队头"。
队列中数据的进出要遵循 “先进先出” 的原则(First In First Out),即最先进队列的数据元素,同样要最先出队列(如入队1、2、3,再进行出队,得到结果仍是1、2、3)
与现实中的“排队”基本一致,较易理解
- 普通队列的问题
对于一个普通的队列,它有一个非常致命的问题:容易造成空间浪费
假设有一个长度为6的队列,我们先入队6个元素,再出队2个元素
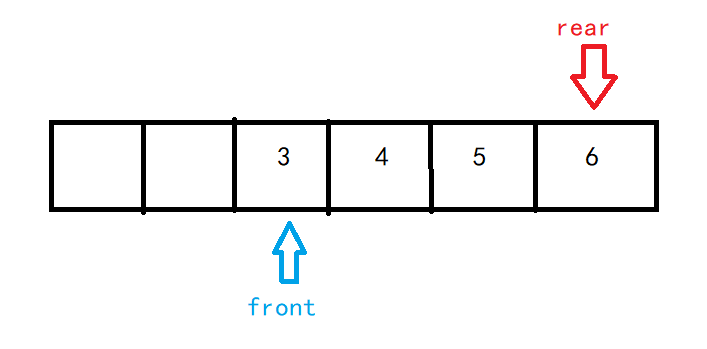
这时我想再插入1个元素,很明显队列中还有2个空间剩余,但是因为rear已经到达极限,我们不能再往队列里插入元素了
此时我们就需要一个循环队列,来解决这个问题,我们在这里定义rear指向队列尾部的后一点
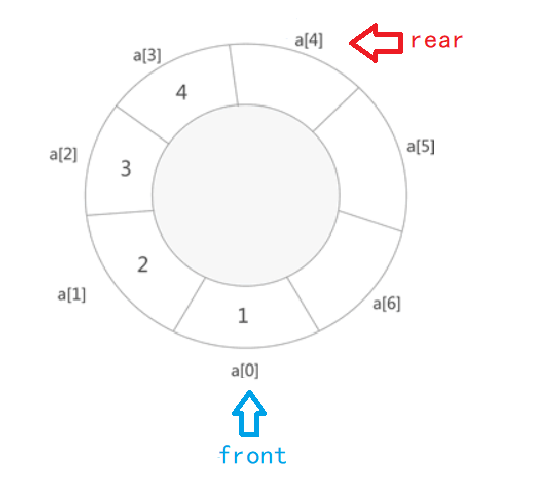
- 为什么rear要往后定义一点?
如果仅仅是原来的定义方法,我们又会遇到一个新问题:我们无法判断队满与队空了(因为队满和队空的条件都为front==rear)
所以我们选择牺牲掉数组中的一个存储空间,此时判断队满的条件是:尾指针的下一个位置和头指针相遇,就说明队列满了,队空即为front==rear - 定义、初始化(顺序队直接以循环队列为例)
对于顺序循环队列,我们对它的初始化需要使它的front、rear值都置为0
对于链队,需要创建一个新链表,front为头结点,初始化read都指向头结点,头结点的next为空(采用带头结点的链表)
初始化的代码较简单,不赘述
- 什么是队列?
typedef struct SeQueue //顺序循环队列
{
int data[MaxSize]; //MaxSize代表队的元素最大数量
int front, rear; //指向队首、队尾后一点
};
typedef struct //链队内部
{
int data;
struct queue* next; //后继节点指针
} queue;
typedef struct LiQueue //保存链队头尾指针
{
queue *front;
queue *rear;
}
- 判断队列是否为空
顺序循环队列的队空条件在上文已有提及,即头尾相同
链队的队空条件仍为头结点的next结点为空(因为使用的时带头结点的链表)
bool QueueEmpty1(SeQueue* Q) //判断顺序循环队列是否为空,为空返回true,不空返回false
{
if (Q->front == Q->rear) //顺序栈为空的条件
return true;
return false;
}
bool QueueEmpty2(LiQueue* Q) //判断链队是否为空,为空返回true,不空返回false
{
if (Q->front->next == NULL) //链队为空的条件
return true;
return false;
}
- 判断队列是否已满
顺序循环队列的队满条件较为特殊,需要留意一下
链队不会有队满的问题,故跳过
bool QueueFull(LiQueue* Q) //判断顺序循环队列是否满了,为满返回true,不满返回false
{
if ((Q->rear + 1) % MaxSize == Q->front) //队满条件,特别注意取余
return true;
return false;
}
- 入队
同样的,对顺序循环队列首先判断队列是否为满,然后再插入,且要注意rear值不只是简单+1,略有不同
链队采用尾插法实现入队即可
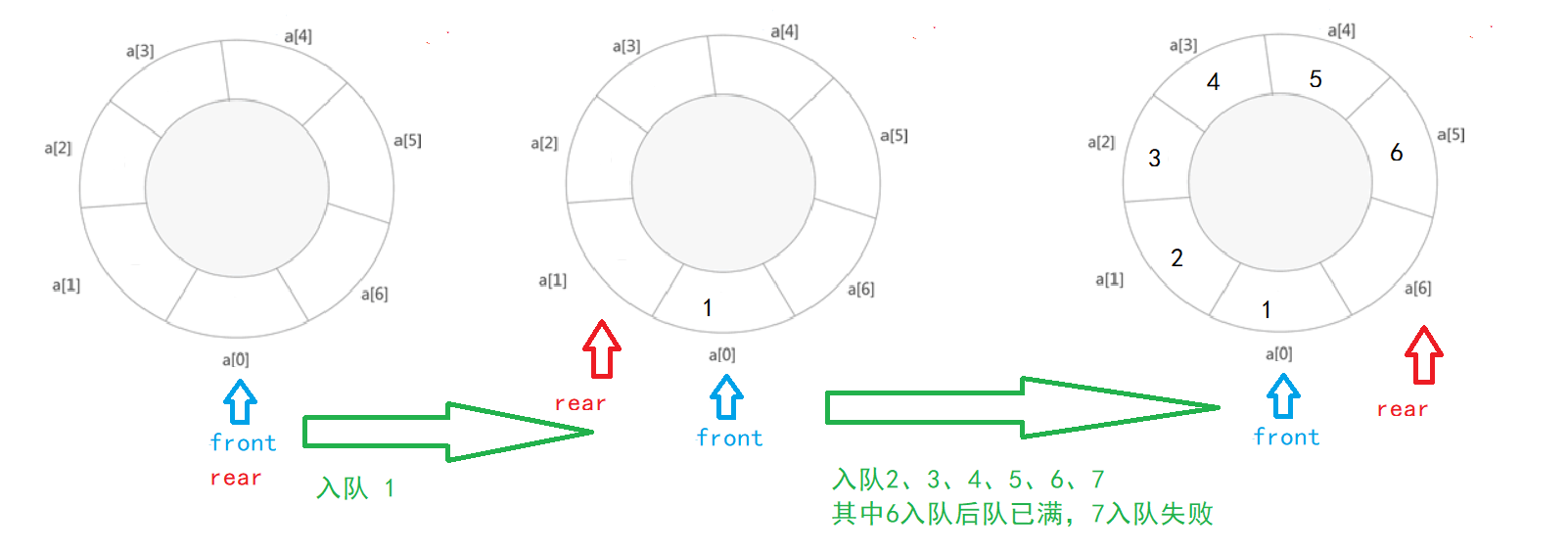

bool enQueue1(SeQueue *Q, int x) //入队元素x
{
if (QueueFull(Q) == true) //队满
{
return false;
}
Q->data[Q->rear] = x; //先入队,再更改rear
Q->rear = (Q->rear + 1) % MaxSize; //特别注意这里,这是为了达成循环的效果
return true;
}
bool enQueue2(LiQueue &Q, int x) //链队
{
queue *temp = new queue; //临时节点
temp->data = x;
temp->next = NULL;
Q->rear->next = temp; //尾插法
Q->rear = temp; //队尾指向新的结点
return true;
}
- 出队
和栈一样,都要先判断队是否为空再进行出列
循环队列的front变化方式需要注意,而链队要注意只有一个元素时删除的情况
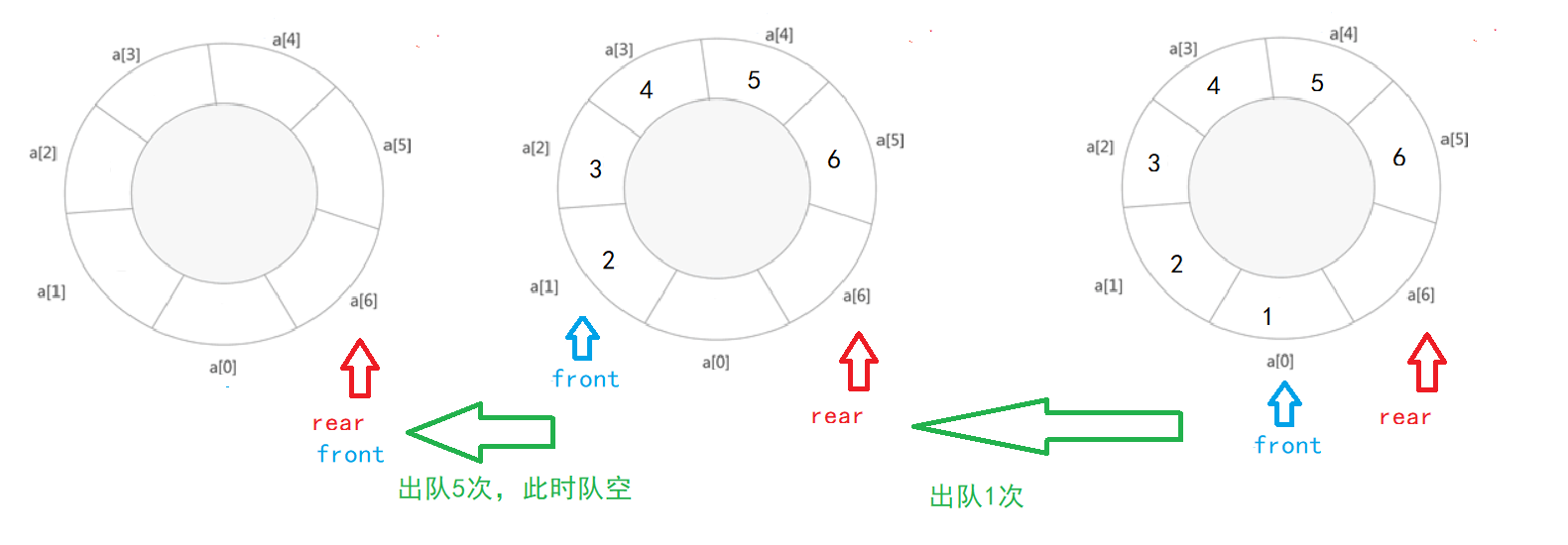
bool deQueue(SeQueue *Q, int &e) //出队,并将原队首的值给e
{
if(EmptyQueue1(Q) == true) //队空
{
return false;
}
e = Q->data[Q->front]; //记录队首的值
Q->front = (Q->front + 1) % MaxSize; //实现循环
return true;
}
bool deQueue2(LiQueue &Q, int &e) //链队,直接取
{
queue *temp = new queue;
if(EmptyQueue2(Q) == true) //队空
{
return false;
}
e = Q->front->next->data; //队首的值
temp = Q->front->next; //保存队首结点
Q->front->next = temp->next;
if (temp == Q->rear) //队列中只有一个元素
Q->front = Q->rear; //队列置空
delete temp; //释放结点内存
return true;
}
- queue库
- push(e):向队尾插入元素e
- pop():删除队首元素
- size():返回队列的大小
- empty():若队列为空返回true,否则返回false
- front():返回队首元素
- back():返回队尾元素
- 队列的应用
- 寻找最短迷宫路径 PTA7-8
- 求解过程简单的伪代码(初始化过程跳过)
- 寻找最短迷宫路径 PTA7-8
while 队列不空 do
{
qu.front++; //出队
读取队首坐标
if 队首坐标即为终点坐标 then
找到出口,输出答案
end if
for I=0 to 4 do
根据i为1、2、3、4,分别记往上下左右走后的坐标
if 走后的坐标没有走过 then
将该方块坐标入队,且它的前驱为qu.front
记录该方块走过
end if
end for
}

- 图片说明
- 用图片说明7-8中例图的部分情况,其中该图中,同一行的步数是相同的(有点像树)
- 可以看的出来,使用队列解决迷宫问题,即使遇到岔路,它也会同时往下走 ,一边岔路走一格,一边岔路走一格这样
- 也就可以知道,首先遇到的终点的一端,倒推回去一定就是最短的路线(例如路线A三十步到达终点,B路线五十步也能到达终点,那么路线A遇到终点的下标一定小于B)
- 和栈走迷宫有什么区别?
- 栈走迷宫使用的是深度优先搜索(DFS),队列走迷宫使用的是广度优先搜索(BFS)
- 说的简单点:栈走迷宫,会一条路走到黑,走到无路可走,才会返回去找其他路
- 而队列则是一层一层向外找可以走的点,同时在多条岔路上找路的感觉
- 例如例题中的图,使用栈就会停在第一个路口,先在右上角打转,直到全部路都走不了了才往下走
1.2 学习体会
- 进入了栈与队列的学习,虽然仍在线性表的范围内,但能明显的感觉到题目难度的变化,相信在接下来的章节中这个变化会更加明显
- 发现了库函数真的很好用!不过还是要注意不能忘了原始的写法
- 对栈和队列没有很特别的认识,拿桶和排队举例子就很容易理解了
- 代码质量有所下降,还不能非常熟练的运用各种库函数,这点有反映在PTA题目中,是接下来要重视一下的点
Q2.PTA实验作业
2.1 表达式转换
2.1.1 代码截图
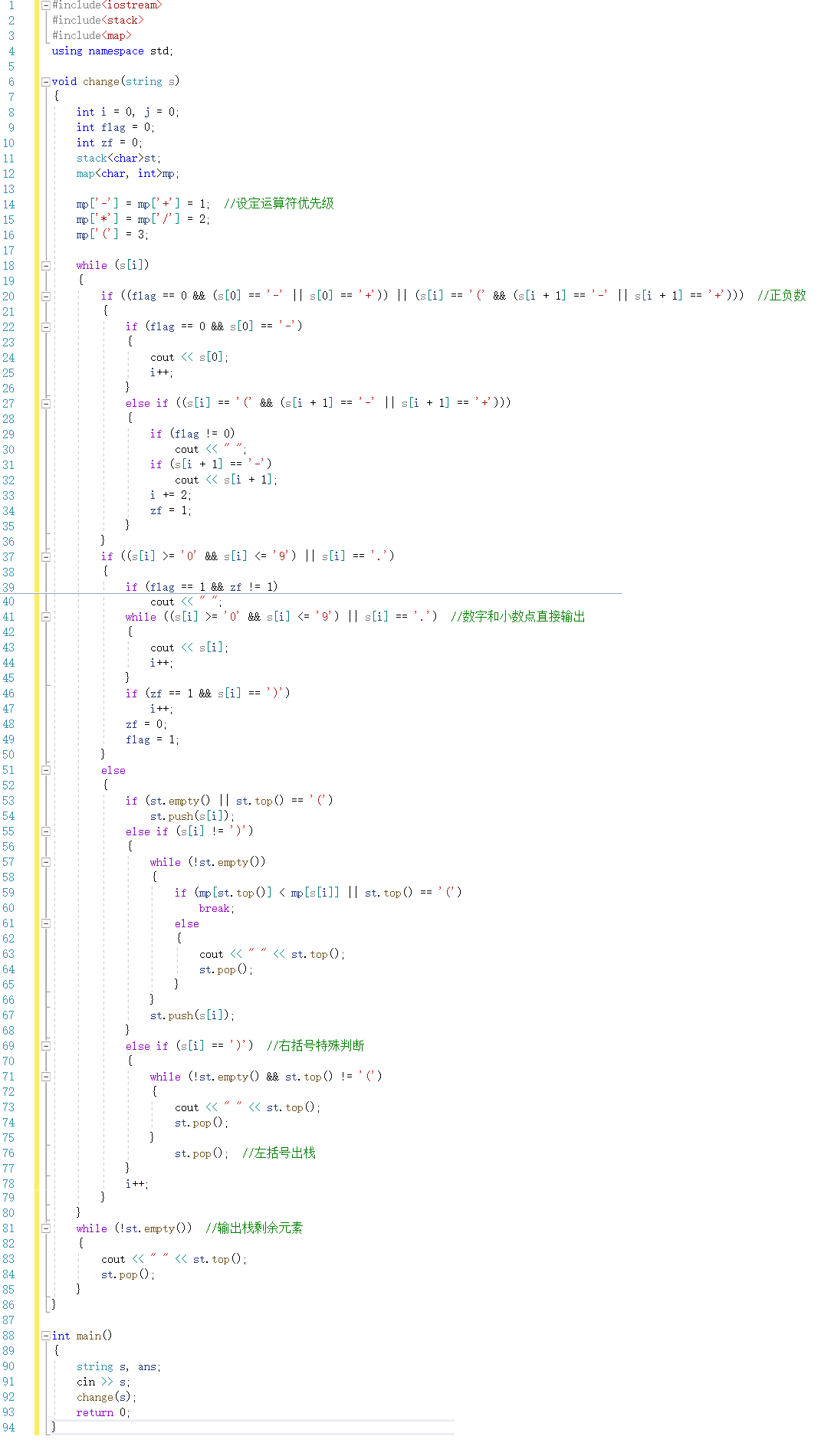
2.1.2 PTA提交列表及说明
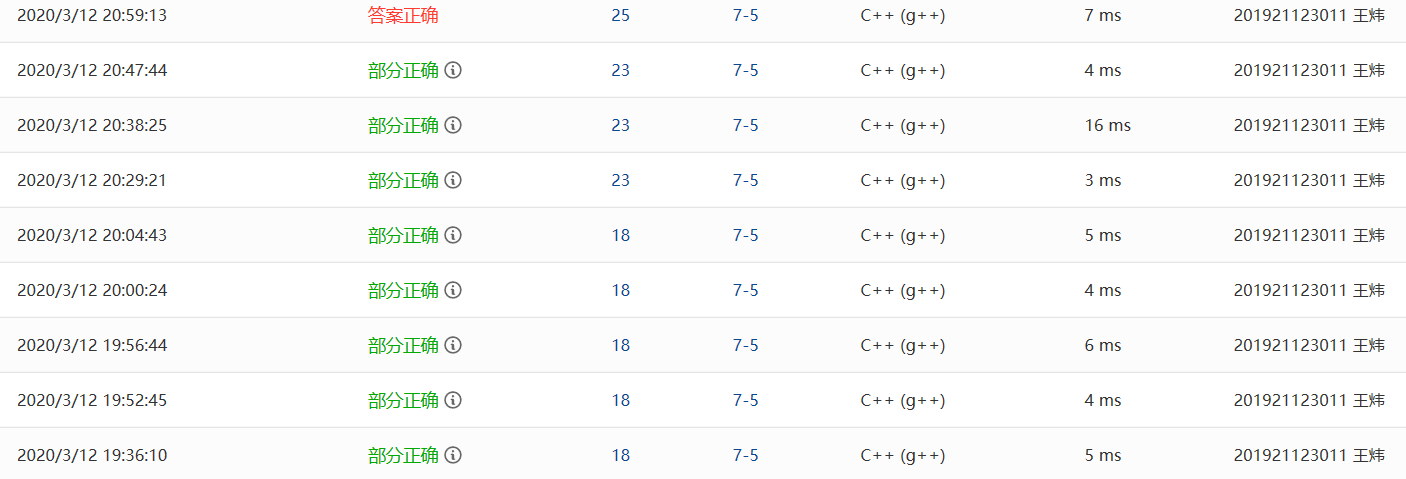
- 1.18分部分正确:嵌套括号、运算数前正负号答案错误,一开始在除了右括号以外的运算符,要根据运算符优先级入栈出栈时,没有考虑到栈顶元素为左括号时的状况,导致将左括号也进行了出栈操作以至于产生了错误,后来添加了对栈顶元素是否为左括号的判断
- 2.18分部分正确:对于(-1)这种负数,没有处理好右括号,导致其会一直出栈到栈空,后来添加了在输出正负数后立马处理右括号的代码
- 3.23分部分正确:运算数前有正负号答案错误,对正负数的判断只写了左括号后为加减号的可能性,没有考虑到如果第一个数就为正负数的话就没有括号的情况,单独增添了对第一个符号是否时正负号的判断
- 4.23分部分正确:遇到正数将加号也一并输出了(如(+3)输出+3),询问后得知正号不需要输出,于是将该部分代码修改为只输出负数的负号
2.2 银行排队问题之单窗口“夹塞”版
2.2.1 代码截图
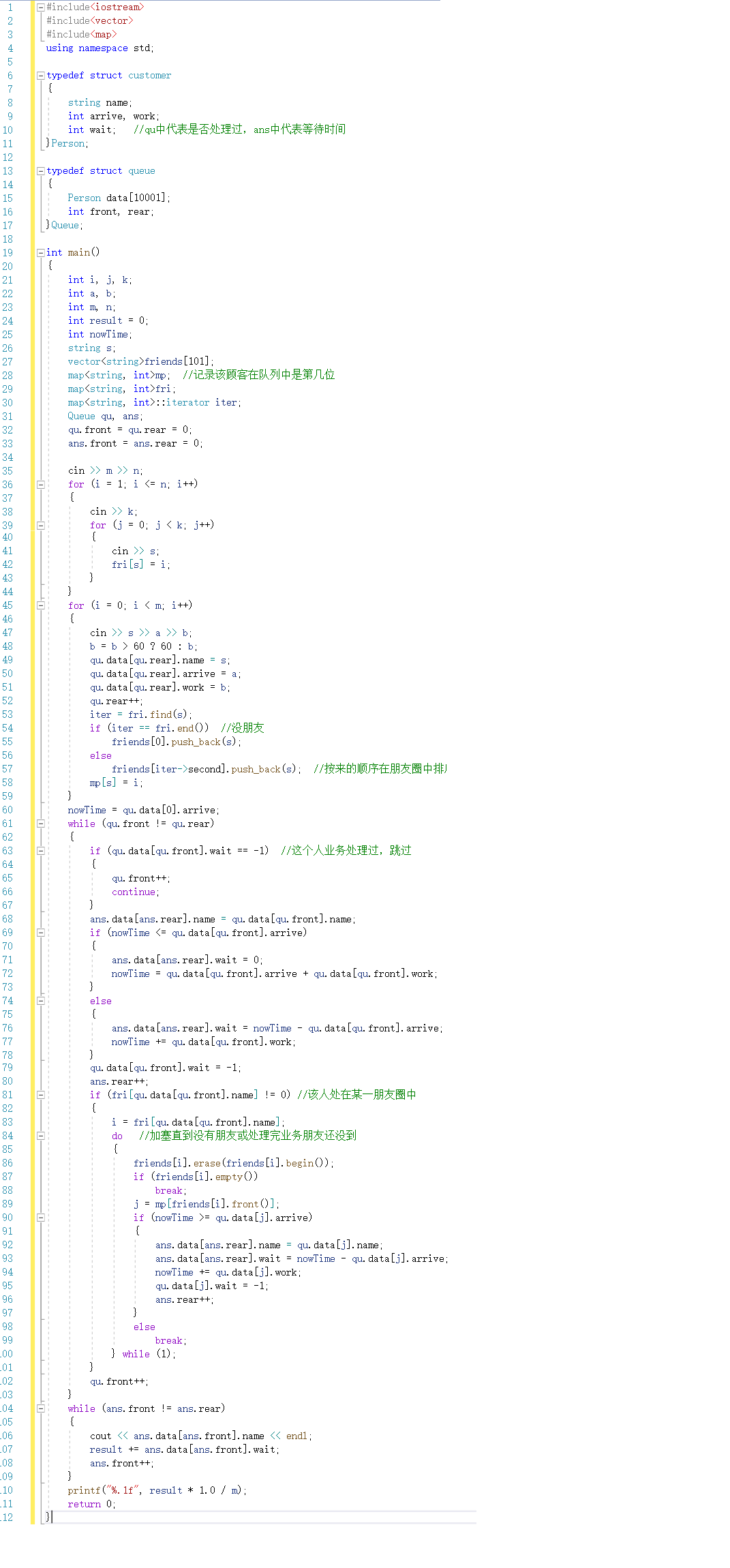
2.2.2 PTA提交列表及说明
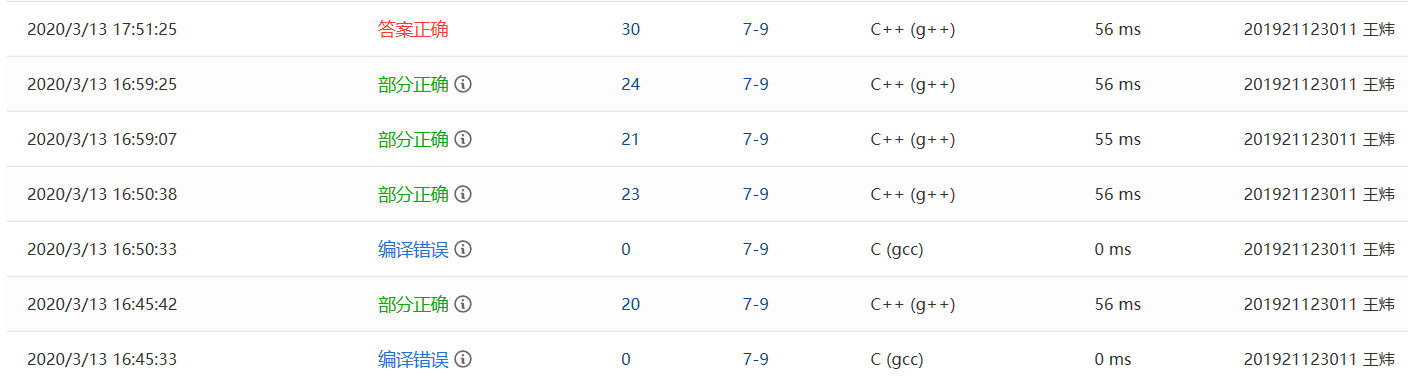
- 1.编译错误:PTA莫名其妙会自己把编译器从C++换成C
- 2.部分正确:一开始仅前2个测试点、一名顾客测试点通过,大规模数据测试点超时
朋友来时队首正好完成/朋友来时原来队首朋友走了的测试点未通过,起初认为这两个测试点都需要重新排队,将中间循环>改为>=后通过 - 3.部分正确:窗口空余一段时间等待下一位测试点,一开始没有考虑这种情况,时间直接从0开始,时间只是工作时间叠加,到达时间大于等待时间就不需要等待等等错误。后来修改了一个变量nowTime用于记录当前时间,开始时为第一个顾客的到达时间,当nowTime小于顾客到达时间时就重置为顾客到达时间,顾客的等待时间即为nowTime减去到达时间,经过这些更改后2名顾客的测试点也一并通过了
- 4.部分正确:大规模数据超时:一开始采用两层循环,时间复杂度为O(n^2),数据多就超时了,后来新添加了一个map,以顾客的名字为key记录顾客在队列中是第几位,并将其运用到代码中,将时间复杂度减少到了O(n),将上条问题解决后一并通过了该测试点,通过了本题
- 5.其他问题:没有用上queue库,做法写作队列读作数组……代码还可以简化
Q3.阅读代码
3.1 栈排序
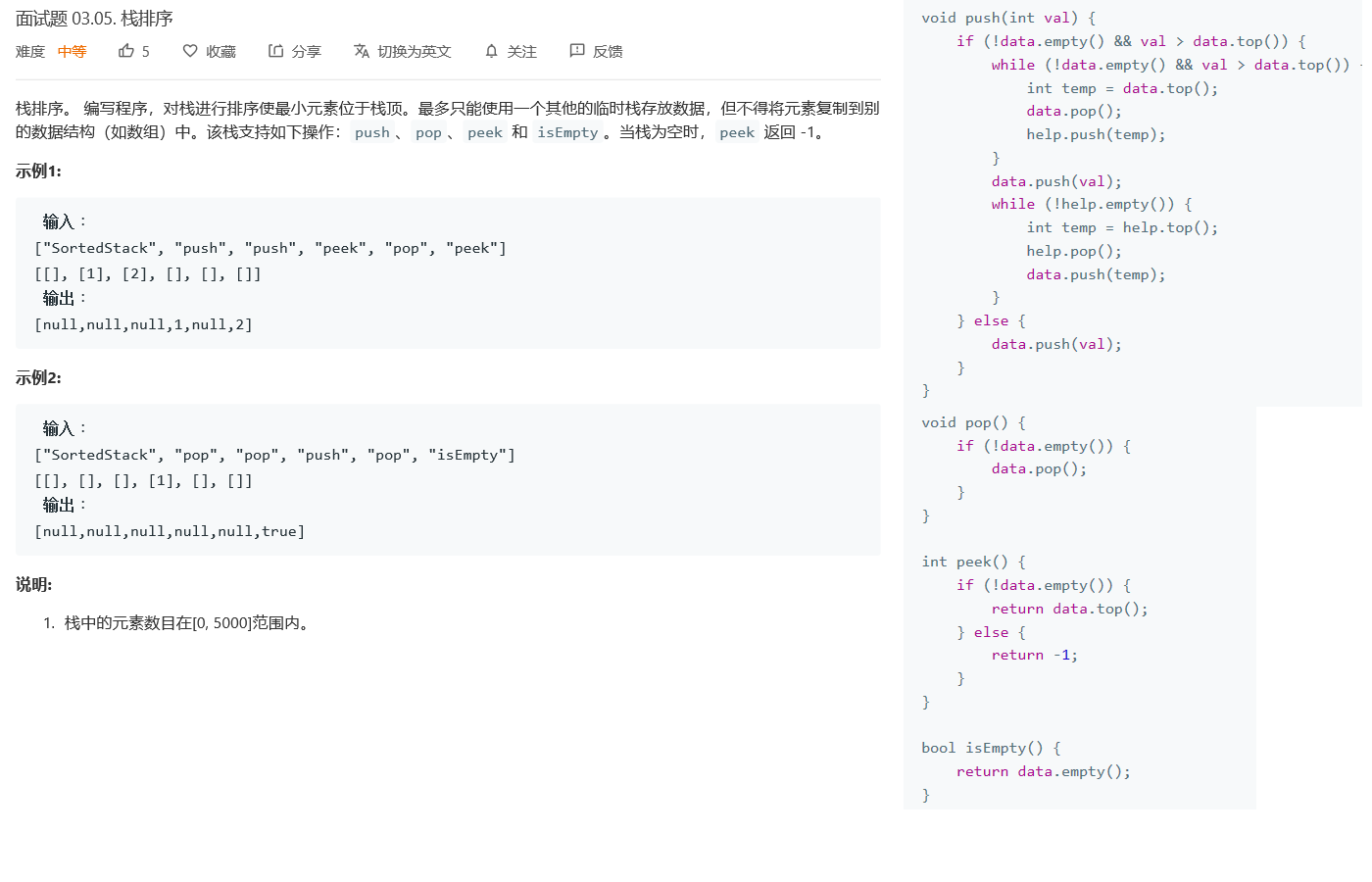
3.1.1 设计思路
本题设计思路较简单,需要保持栈的栈顶元素为栈中最小的元素
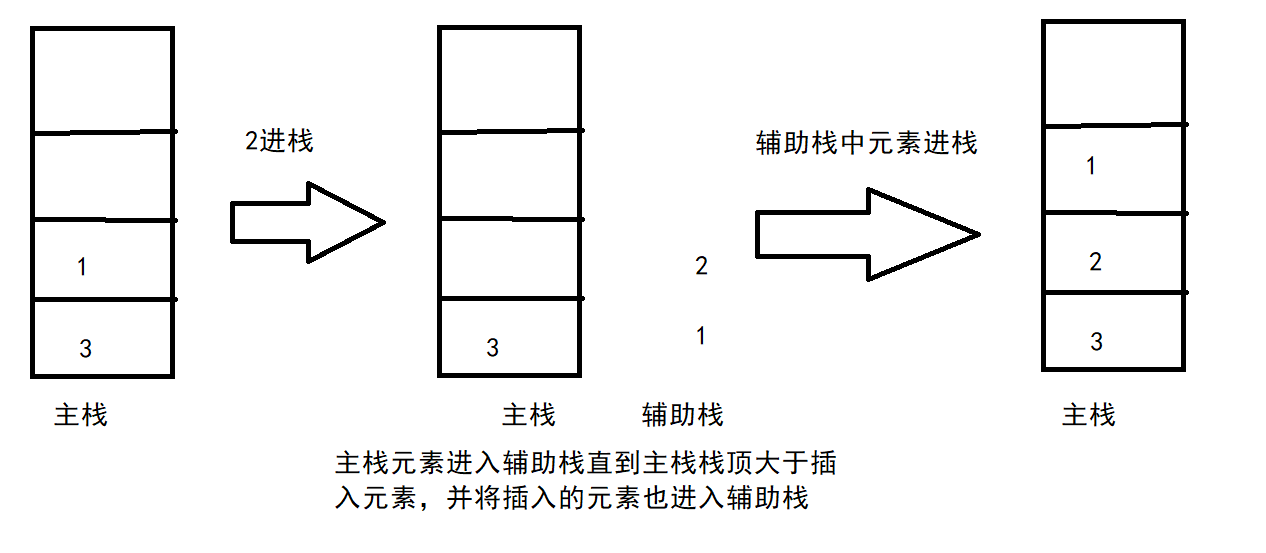
假设已有一个符合要求的栈(1,3)现在想要插入数据2
发现2大于栈顶元素1-->建立辅助栈,1入辅助栈,出主栈-->2小于栈顶元素3,2进入辅助栈-->将辅助栈中元素再进入主栈,即得到答案
图示如下
时间复杂度为O(n),空间复杂度为O(n)
3.1.2 伪代码
//本题其他函数代码较简单,这里就只放入栈的代码了
void push(int val) {
if 主栈非空且主栈栈顶元素小于插入元素 then
while 主栈非空且主栈栈顶元素小于插入元素 do
记录主栈栈顶元素
主栈出栈、辅助栈入栈
end while
将插入元素也放入辅助栈
while 辅助栈非空 do
记录辅助栈栈顶元素
辅助栈出栈、主栈入栈
end while
else 栈顶元素大于插入元素
插入元素直接入栈
end if
}
3.1.3 运行结果
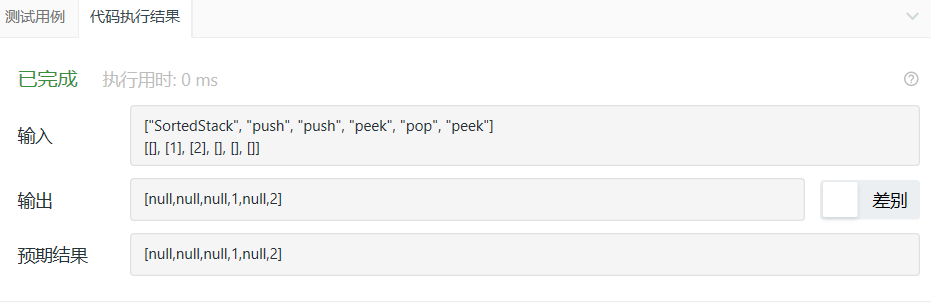
3.1.4 分析
- 本题要求只能用额外的一个辅助栈来达到目的,可能是本题要求稍高一点的地方,但也没有特别困难
- 巧妙运用两个栈来回入栈、出栈的特性,可以使原来正向排列的栈变成反向
- 在题解中还有看到使用vector库函数的做法,但是它运用到了sort函数,导致时间复杂度上不如该做法
3.2 最大频率栈
3.2.1 设计思路
本题需改变出栈操作,移除栈中出现最频繁的数,若多个数字出现次数相同,则移出离栈顶最近的元素
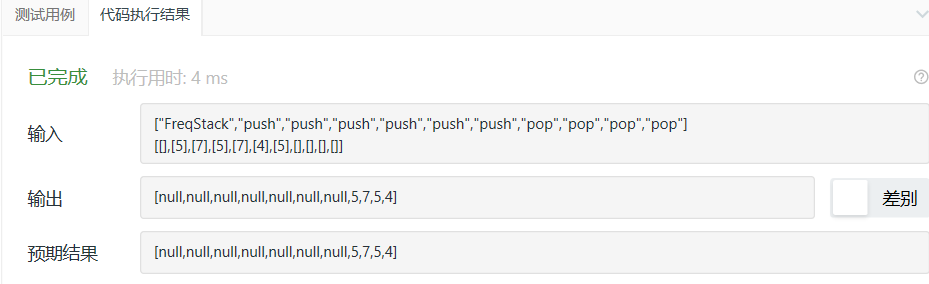
假设有栈(5,7,5,7,4,5,从左到右为栈底到栈顶)
第一次pop:5出现次数最多,移除5,此时栈(5,7,5,7,4)
第二次pop:5、7出现次数一样多,但7离栈顶近,移出7,此时栈(5,7,5,4)
第三次pop:5出现次数最多,移除5,此时栈(5,7,4)
第四次pop:5、7、4出现次数一样多,4为栈顶,即移除4
第五、六次pop移除7、5
该题解使用了两个map,一个map是数值对应出现次数,一个map是出现次数对应栈,对题解代码的说明在下面
时间复杂度为O(1),空间复杂度为O(n)
3.2.2 伪代码
void push(int x) {
数字x出现次数+1
在最大出现次数和数字x的出现次数中取最大
向第 (x的出现次数) 个栈入栈元素x
}
int pop() {
取x为第 (最大出现次数) 个栈的栈顶元素
对应栈出栈
数字x的出现次数减1
if(对应出现次数的栈已空) 最大出现次数减1;
return x;
}
3.2.3 运行结果
3.2.4 分析
- 本题的第二个map我觉得是使用的最巧妙的,非常完美的空间换时间做法
- 首先是第一个map,freq,单纯的记录某个数字的出现次数,很正常
- 最难也最巧妙的是第二个map,group,其映射值是一个栈,它将所有出现次数相同的数字又放到一个栈中,完美解决了“出现次数相同时,输出离栈最近的元素”的要求
- 举个栗子,有数字1,2,1,2,3入栈(栈底->栈顶),其中1和2的出现次数一样多,但是因为第二个1更早出现,所以1先进入了group[2]的栈
之后又遇到了第二个2,2在1之后进入了group[2]的栈,所以group[2]的栈从栈顶到栈底存着2、1
此时出栈,就得到2,出现次数为2的栈还剩下1,跟着后出栈,此时已有答案2 1
这时出现次数为2的栈已空,最大出现次数减1得到1
出现次数为1的栈按照栈底到栈顶的排序为1、2、3,所以接着输出为3、2、1
所以得到最终答案2 1 3 2 1 - 本题题解作者对map函数与栈的结合使用十分精彩,我认为是这篇题解代码最优秀的地方