最近几天打算认真复习LCT,毕竟以前只会板子。正好也可以学点新的用法,这里就用来写做题笔记吧。这个分类比较混乱,主要看感觉,不一定对;
维护森林的LCT
就是最普通,最一般那种的LCT啦。这类题目往往就是用LCT维护森林,从而快速的实现一些链上操作;其中,某些题只是维护一棵形态固定的树,用树剖也可以做,复杂度 $nlog^2n$,如果使用LCT则变成了 $nlog n$;有的题目涉及断边连边,就必须使用LCT了。这次复习做的前几道题都属于这种,这几道题的难点其实不在LCT上,只要会敲模板就OK了,可以稍微练习码力。正好这次就顺便把以前做过的题一起整理一下吧~一个可能会一时糊涂理解不了的地方:当我说“每个点记录某某信息时”,指的是维护Splay上的子树信息,但是由于Splay本质上是在维护树链,所以split一段路径后,splay的根节点记录的就是树链信息了。
[模板]Link Cut Tree
题意概述:断边加边,修改点权,询问路径异或和;
是一道小清新的模板题呢,只用到了一些基础的操作,没有区间修改这类稍微复杂的东西。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # define R register int 6 # define getchar() (S==T&&(T=(S=BB)+fread(BB,1,1<<15,stdin),S==T)?EOF:*S++) 7 8 using namespace std; 9 10 const int maxn=300010; 11 int n,m,opt,x,y; 12 int v[maxn],ch[maxn][2],f[maxn],sta[maxn],Tp,s[maxn],rev[maxn]; 13 char BB[1 << 18], *S = BB, *T = BB; 14 15 int read() 16 { 17 R x=0; 18 char c=getchar(); 19 while (!isdigit(c)) c=getchar(); 20 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 21 return x; 22 } 23 24 bool rt (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } //x是所在splay的根吗? 25 void update (int x) { s[x]=v[x]^s[ ch[x][0] ]^s[ ch[x][1] ]; } 26 void swp (int x) { rev[x]^=1; swap(ch[x][0],ch[x][1]); } 27 void pushdown (int x) 28 { 29 if(rev[x]==0) return ; 30 if(ch[x][0]) swp(ch[x][0]); 31 if(ch[x][1]) swp(ch[x][1]); 32 rev[x]=0; 33 } 34 35 void rotate (int x) 36 { 37 int fx=f[x],ff=f[fx],k=(ch[fx][1]==x),t=ch[x][k^1]; 38 if(rt(fx)) ch[ff][ ch[ff][1]==fx ]=x; 39 ch[fx][k]=t,ch[x][k^1]=fx,f[fx]=x,f[x]=ff; 40 if(t) f[t]=fx; 41 update(fx); 42 } 43 44 void splay (int x) //把x转到自己所在splay的根上去 45 { 46 Tp=0,sta[++Tp]=x; 47 int y=x; 48 while(rt(y)) sta[++Tp]=(y=f[y]); 49 for (R i=Tp;i>=1;--i) pushdown(sta[i]); 50 int fx,ff; 51 while(rt(x)) 52 { 53 fx=f[x],ff=f[fx]; 54 if(rt(fx)) rotate(((ch[fx][0]==x)!=(ch[ff][0]==fx))?x:fx); 55 rotate(x); 56 } 57 update(x); 58 } 59 60 int ws (int x) { return (ch[ f[x] ][1]==x); } //x是父亲的哪个孩子? 61 void access (int x) 62 { 63 for (R y=0;x;y=x,x=f[x]) 64 splay(x),ch[x][1]=y,update(x); 65 } 66 67 void change_root (int x) { access(x); splay(x); swp(x); } 68 int find (int x) 69 { 70 access(x),splay(x); 71 while(ch[x][0]) pushdown(x),x=ch[x][0]; 72 return x; 73 } 74 75 void link (int x,int y) 76 { 77 change_root(x); 78 if(find(y)!=x) f[x]=y; 79 } 80 81 void cut (int x,int y) 82 { 83 change_root(x); 84 if(find(y)!=x||f[x]!=y||ch[x][1]) return ; 85 f[x]=ch[y][0]=0; 86 update(y); 87 } 88 89 void split (int x,int y) 90 { 91 change_root(x); 92 access(y),splay(y); 93 } 94 95 void write (int x) 96 { 97 if(x>=10) write(x/10); 98 putchar(x%10+'0'); 99 } 100 101 int main() 102 { 103 n=read(),m=read(); 104 for (R i=1;i<=n;++i) v[i]=read(); 105 for (R i=1;i<=m;++i) 106 { 107 opt=read(),x=read(),y=read(); 108 if(opt==0) split(x,y),write(s[y]),putchar(' '); 109 else if(opt==1) link(x,y); 110 else if(opt==2) cut(x,y); 111 else if(opt==3) splay(x),v[x]=y; 112 } 113 return 0; 114 }
洞穴勘探
题意概述:断边加边,询问连通性;

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # define R register int 6 7 using namespace std; 8 9 const int maxn=10005; 10 int n,m,x,y,F[maxn],ch[maxn][2],t[maxn],st[maxn],Tp; 11 char c[10]; 12 13 inline bool isnt_rt (int x) { return ch[ F[x] ][0]==x||ch[ F[x] ][1]==x; } 14 inline void rev (int x) { swap(ch[x][0],ch[x][1]); t[x]^=1; } 15 inline void pushdown (int x) { if(t[x]) rev(ch[x][0]),rev(ch[x][1]),t[x]=0; } 16 inline int D (int x) { return ch[ F[x] ][1]==x; } 17 18 inline void rotate (int x) 19 { 20 int f=F[x],g=F[f],dx=D(x),df=D(F[x]); 21 int k=ch[x][dx^1]; 22 if(isnt_rt(f)) ch[g][df]=x; 23 ch[f][dx]=k; 24 ch[x][dx^1]=f; 25 if(k) F[k]=f; 26 F[f]=x; F[x]=g; 27 } 28 29 inline void splay (int x) 30 { 31 // printf("splay(%d) ",x); 32 int t=x,f,g; 33 st[++Tp]=t; 34 while (isnt_rt(t)) st[++Tp]=F[t],t=F[t]; 35 while (Tp) pushdown(st[Tp]),Tp--; 36 while (isnt_rt(x)) 37 { 38 f=F[x],g=F[f]; 39 if(isnt_rt(f)) 40 { 41 if(D(x)==D(f)) rotate(f); 42 else rotate(x); 43 } 44 rotate(x); 45 } 46 } 47 48 inline void access (int x) 49 { 50 // printf("access(%d) ",x); 51 for (int y=0;x;y=x,x=F[x]) 52 splay(x),ch[x][1]=y; 53 } 54 55 inline void makeroot (int x) 56 { 57 // printf("makeroot(%d) ",x); 58 access(x); 59 splay(x); 60 rev(x); 61 } 62 63 inline int findroot (int x) 64 { 65 // printf("findroot(%d) ",x); 66 access(x),splay(x); 67 while(ch[x][0]) pushdown(x),x=ch[x][0]; 68 splay(x); 69 return x; 70 } 71 72 inline void link (int x,int y) 73 { 74 // printf("link(%d %d) ",x,y); 75 makeroot(x); 76 if(findroot(y)!=x) F[x]=y; 77 access(y); 78 } 79 80 inline void cut (int x,int y) 81 { 82 // printf("cut(%d %d) ",x,y); 83 makeroot(x); 84 access(y); 85 splay(y); 86 F[x]=0,ch[y][0]=0; 87 } 88 89 int main() 90 { 91 scanf("%d%d",&n,&m); 92 for (R i=1;i<=m;++i) 93 { 94 scanf("%s",c+1); 95 scanf("%d%d",&x,&y); 96 if (c[1]=='Q') 97 { 98 if(findroot(x)==findroot(y)) printf("Yes "); 99 else printf("No "); 100 } 101 else if (c[1]=='C') 102 link(x,y); 103 else if (c[1]=='D') 104 cut(x,y); 105 } 106 return 0; 107 }
Tree II
题意概述:需要支持路径乘,路径加,断边加边,询问路径和;$n<=10^5$
其实还是...比较简单的吧...就是在普通的LCT上打打标记(乘法,翻转,加法),维护一些信息(子树和,子树大小),稍微有点难写。不要忘了Splay时标记要从上往下放!一个小坑:模数虽小,乘法时也要开longlong。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # define R register int 6 # define ll unsigned int 7 8 using namespace std; 9 10 const int maxn=100005; 11 const int mod=51061; 12 int n,q,x,y,db; 13 int ch[maxn][2],f[maxn],r[maxn],st[maxn]; 14 ll da[maxn],dm[maxn],s[maxn],siz[maxn],v[maxn]; 15 char opt[10]; 16 17 int read() 18 { 19 R x=0; 20 char c=getchar(); 21 while (!isdigit(c)) c=getchar(); 22 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 23 return x; 24 } 25 26 bool isntroot (int x) { return ch[ f[x] ][0]==x||ch[ f[x] ][1]==x; } 27 28 int D (int x) { return ch[ f[x] ][1]==x; } 29 30 void update (int x) 31 { 32 int l=ch[x][0],r=ch[x][1]; 33 siz[x]=(siz[l]+siz[r]+1)%mod; 34 s[x]=(s[l]+s[r]+v[x])%mod; 35 } 36 37 inline void turn (int x) 38 { 39 r[x]^=1; 40 swap(ch[x][0],ch[x][1]); 41 } 42 43 inline void rev (int x) 44 { 45 r[x]=0; 46 if(ch[x][0]) turn(ch[x][0]); 47 if(ch[x][1]) turn(ch[x][1]); 48 } 49 50 inline void pushdown (int x) 51 { 52 if(dm[x]==1&&da[x]==0&&r[x]==0) return; 53 if(r[x]) rev(x); 54 int l=ch[x][0],r=ch[x][1]; 55 if(l) 56 { 57 v[l]=(v[l]*dm[x]+da[x])%mod; 58 s[l]=(s[l]*dm[x]+siz[l]*da[x])%mod; 59 dm[l]=dm[l]*dm[x]%mod; 60 da[l]=(da[l]*dm[x]+da[x])%mod; 61 } 62 if(r) 63 { 64 v[r]=(v[r]*dm[x]+da[x])%mod; 65 s[r]=(s[r]*dm[x]+siz[r]*da[x])%mod; 66 dm[r]=dm[r]*dm[x]%mod; 67 da[r]=(da[r]*dm[x]+da[x])%mod; 68 } 69 dm[x]=1; da[x]=0; 70 } 71 72 void rotate (int x) 73 { 74 if(db) printf("rotate(%d) ",x); 75 int F=f[x],g=f[F],d=D(x),df=D(F); 76 pushdown(F); pushdown(x); 77 int k=ch[x][d^1]; 78 ch[F][d]=k; 79 ch[x][d^1]=F; 80 if(isntroot(F)) ch[g][df]=x; 81 if(k)f[k]=F; f[F]=x; f[x]=g; 82 update(F); update(x); 83 } 84 85 void splay (int x) 86 { 87 if(db) printf("splay(%d) ",x); 88 int y=x,tp=0; 89 st[++tp]=x; 90 while(isntroot(y)) st[++tp]=f[y],y=f[y]; 91 while(tp) pushdown(st[tp]),tp--; 92 while(isntroot(x)) 93 { 94 int F=f[x],g=f[g]; 95 if(!isntroot(F)) rotate(x); 96 else if(D(x)==D(F)) rotate(F),rotate(x); 97 else rotate(x),rotate(x); 98 } 99 } 100 101 void access (int x) 102 { 103 if(db) printf("access(%d) ",x); 104 int y=0; 105 while(x) 106 { 107 splay(x); 108 ch[x][1]=y; 109 update(x); 110 y=x; x=f[x]; 111 } 112 } 113 114 void make_root (int x) 115 { 116 if(db) printf("make_root(%d) ",x); 117 access(x); 118 splay(x); 119 turn(x); 120 } 121 122 void spilt (int x,int y) 123 { 124 if(db) printf("spilt(%d,%d) ",x,y); 125 make_root(x); 126 access(y); 127 splay(y); 128 } 129 130 void link (int x,int y) 131 { 132 if(db) printf("link(%d,%d) ",x,y); 133 make_root(x); 134 f[x]=y; 135 } 136 137 void cut (int x,int y) 138 { 139 if(db) printf("cut(%d,%d) ",x,y); 140 spilt(x,y); 141 f[x]=0; ch[y][0]=0; 142 update(y); 143 } 144 145 void mul (int x,int y,int c) 146 { 147 c%=mod; 148 spilt(x,y); 149 v[y]=v[y]*c%mod; s[y]=s[y]*c%mod; 150 da[y]=da[y]*c%mod; dm[y]=dm[y]*c%mod; 151 } 152 153 void add (int x,int y,int c) 154 { 155 c%=mod; 156 spilt(x,y); 157 v[y]=(v[y]+c)%mod; s[y]=(s[y]+siz[y]*c)%mod; 158 da[y]=(da[y]+c)%mod; 159 } 160 161 int main() 162 { 163 scanf("%d%d",&n,&q); 164 for (R i=1;i<=n;++i) 165 v[i]=siz[i]=s[i]=dm[i]=1; 166 for (R i=1;i<n;++i) 167 { 168 x=read(),y=read(); 169 link(x,y); 170 } 171 for (R i=1;i<=q;++i) 172 { 173 int c; 174 scanf("%s",opt); 175 if(opt[0]=='+') 176 { 177 x=read(),y=read(),c=read(); 178 add(x,y,c); 179 } 180 else if(opt[0]=='-') 181 { 182 x=read(),y=read(); 183 cut(x,y); 184 x=read(),y=read(); 185 link(x,y); 186 } 187 else if(opt[0]=='*') 188 { 189 x=read(),y=read(),c=read(); 190 mul(x,y,c); 191 } 192 else if(opt[0]=='/') 193 { 194 x=read(),y=read(); 195 spilt(x,y); 196 printf("%u ",s[y]); 197 } 198 } 199 return 0; 200 }
弹飞绵羊
这道题概述题意后就没啥好做的啦。其实就是每个点向被弹到的点连边,构成一个森林结构,询问时就查一下这个点的深度,是不是很简单呢。

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 5 using namespace std; 6 7 const int maxn=200005; 8 int n,m,t[maxn],opt,F[maxn],ch[maxn][2],siz[maxn],x,y; 9 10 inline int D (int x) { return ch[ F[x] ][1]==x; } 11 inline bool isnt_root (int x) { return ch[ F[x] ][0]==x||ch[ F[x] ][1]==x; } 12 inline void update (int x) { siz[x]=siz[ ch[x][0] ]+siz[ ch[x][1] ]+1; } 13 inline void rotate (int x) 14 { 15 int f=F[x],g=F[f],dx=D(x),df=D(f); 16 int k=ch[x][dx^1]; 17 ch[f][dx]=k; 18 if(isnt_root(f)) ch[g][df]=x; 19 F[f]=x,F[k]=f; 20 ch[x][dx^1]=f; 21 F[x]=g; 22 update(f),update(x); 23 } 24 25 inline void splay (int x) 26 { 27 while(isnt_root(x)) 28 { 29 if(isnt_root(F[x])) 30 rotate((D(x)==D(F[x]))?F[x]:x); 31 rotate(x); 32 } 33 update(x); 34 } 35 inline void access (int x) { for (int y=0;x;y=x,x=F[x]) splay(x),ch[x][1]=y,update(x); } 36 37 inline int read () 38 { 39 R x=0; 40 char c=getchar(); 41 while (!isdigit(c)) c=getchar(); 42 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 43 return x; 44 } 45 46 int main() 47 { 48 scanf("%d",&n); 49 for (R i=1;i<=n;++i) 50 { 51 siz[i]=1; 52 x=read(); 53 if(i+x<=n) F[i]=i+x; 54 } 55 scanf("%d",&m); 56 for (R i=1;i<=m;++i) 57 { 58 opt=read(),x=read(); 59 x++; 60 if(opt==1) 61 { 62 access(x),splay(x); 63 printf("%d ",siz[x]); 64 } 65 else 66 { 67 scanf("%d",&y); 68 access(x),splay(x); 69 ch[x][0]=F[ ch[x][0] ]=0; 70 if(x+y<=n) F[x]=x+y; 71 update(x); 72 } 73 } 74 return 0; 75 }
在美妙的数学王国中畅游
从这里开始难度开始加大了,然而似乎难度不在LCT上...
题意概述:给出一个动态加边删边的森林,每个点上有一个函数,是以下三种函数中的一种 $ax+b,sin(ax+b),e^{ax+b}$ ,$a,b$ 对于每个点不同。同时,也会有单点修改点上函数的操作;给出一些询问,询问对于某个 $x$ ,将它分别带入 $u$ 到 $v$ 的路径上所有函数所得函数值的和。
乍一看这道题很难,其实也确实不算简单。动态加边删边,明示LCT,现在的问题就是怎样快速的计算这些函数;经过观察,可以发现形如 $ax+b$ 的函数显然是很好合并的,这就启示我们把所有函数都变成多项式,因为多项式相加是可以把值相加的。往下翻题面,发现他给出了一个泰勒展开的式子,这证实了上面的猜想:对每个函数进行泰勒展开,用多项式来近似求这些函数值的和。由于多项式是可以合并的,这道题也就迎刃而解了;
在这里,我先把泰勒展开的式子写出来:
$ m sum_{i=0}^nfrac{f^{(i)}(x_0)(x-x_0)^i}{i!}$
显然,$ax+b$就不用泰勒展开了...$e^x,sin(x)$求导不算特别简单,但是基本上知道求导的同学也都知道这些公式吧...
$ m (sin(x))'=cos(x),(cos(x))'=-sin(x)$ $ m(e^x)'=e^x$
那么,$x_0$ 取多少比较合适呢?当然是0啦~,取0多方便啊,首先,$ax+b=b$ 这一点就方便很多,$ax+b-ax_0-b=ax$就更妙了,把 $a^i$ 直接乘进系数里,就可以得到关于 $x$ 的多项式啦;因为分母增长很快,而分子缩小得也很快,所以取前15项就可以完成要求咯。
三叉神经树
这题挺妙的,要稍微观察一下性质;
首先,改变一个输入,可能会被影响的只有从它到根这条路径上的点;如果路径上的某个点没有被影响,那么从它往上就更不会被影响了;再次观察,可以发现,一个输入从0->1,只会将从这里往上连续的一串1变成2,再往上一个数+1,其它的都不变;1->0,只会将从这里往上连续的一串2变成1,再往上一个数-1,其它的都不变;所以说,我们只需要在LCT的每个点上维护从这个点到根的路径上深度最小的非1点位置和非2点位置。区间+1/-1后,所有不是1的都变得不是2了,所有不是2的都变得不是1了,所以只需要交换这两个信息就可以维护了。这道题重在观察,只要这些性质都能看出来,写代码反而变得挺简单了。

1 # include <cstdio> 2 # include <iostream> 3 # include <queue> 4 # define R register int 5 6 using namespace std; 7 8 const int N=500005; 9 int n,q,x,x1,x2,x3; 10 int lk[N*3],tf[N],d[N]; 11 int ch[N][2],f[N],sta[N]; 12 int s[3][N],a[N*3]; 13 int v[N],delta[N],rev[N]; 14 15 int read() 16 { 17 int x=0; 18 char c=getchar(); 19 while (!isdigit(c)) c=getchar(); 20 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 21 return x; 22 } 23 24 void update (int x) 25 { 26 for (R i=1;i<=2;++i) 27 { 28 s[i][x]=s[i][ ch[x][1] ]; 29 if(s[i][x]==0&&v[x]!=i) s[i][x]=x; 30 if(s[i][x]==0) s[i][x]=s[i][ ch[x][0] ]; 31 } 32 } 33 34 void add (int x,int opt) 35 { 36 delta[x]+=opt; v[x]+=opt; 37 swap(s[1][x],s[2][x]); 38 } 39 40 void pushdown (int x) 41 { 42 if(rev[x]) 43 { 44 rev[x]=0; 45 swap(ch[x][0],ch[x][1]); 46 if(ch[x][0]) rev[ ch[x][0] ]^=1; 47 if(ch[x][1]) rev[ ch[x][1] ]^=1; 48 } 49 if(delta[x]) 50 { 51 int t=delta[x]; 52 if(ch[x][0]) add(ch[x][0],t); 53 if(ch[x][1]) add(ch[x][1],t); 54 delta[x]=0; 55 } 56 } 57 58 bool isntroot (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } 59 60 int D (int x) { return ch[ f[x] ][1]==x; } 61 62 void rotate (int x) 63 { 64 int F=f[x],g=f[F]; 65 int dx=D(x),df=D(F); 66 int k=ch[x][dx^1]; 67 ch[F][dx]=k; 68 ch[x][dx^1]=F; 69 if(ch[g][df]==F) ch[g][df]=x; 70 if(k) f[k]=F; f[F]=x; f[x]=g; 71 update(F); 72 update(x); 73 } 74 75 void splay (int x) 76 { 77 int y=x,tp=0; sta[++tp]=x; 78 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 79 for (R i=tp;i>=1;--i) pushdown(sta[i]); 80 while(isntroot(x)) 81 { 82 int t=f[x]; 83 if(!isntroot(t)) rotate(x); 84 else if(D(t)==D(x)) rotate(t),rotate(x); 85 else rotate(x),rotate(x); 86 } 87 } 88 89 void access (int x) 90 { 91 int y=0; 92 while(1) 93 { 94 splay(x); 95 ch[x][1]=y; 96 update(x); 97 y=x; x=f[x]; 98 if(!x) return; 99 } 100 } 101 102 void makeroot (int x) 103 { 104 access(x); splay(x); 105 rev[x]^=1; 106 } 107 108 void link (int x,int y) { makeroot(x); f[x]=y; } 109 110 void split (int x,int y) 111 { 112 makeroot(x); 113 access(y); 114 splay(y); 115 } 116 117 void topu() 118 { 119 queue<int> q; 120 for (R i=1;i<=n;++i) 121 if(d[i]==0) q.push(i); 122 int beg; 123 while(q.size()) 124 { 125 beg=q.front(); q.pop(); 126 if(beg==1) return; 127 v[ tf[beg] ]+=(v[beg]>=2); 128 d[ tf[beg] ]--; 129 if(d[ tf[beg] ]==0) q.push(tf[ beg ]); 130 } 131 } 132 133 int main() 134 { 135 n=read(); 136 for (R i=1;i<=n;++i) 137 { 138 x1=read(); x2=read(); x3=read(); d[i]=3; 139 if(x1<=n) tf[x1]=i; else lk[x1-n]=i; 140 if(x2<=n) tf[x2]=i; else lk[x2-n]=i; 141 if(x3<=n) tf[x3]=i; else lk[x3-n]=i; 142 } 143 for (R i=1;i<=2*n+1;++i) 144 { 145 a[i]=read(); 146 v[ lk[i] ]+=a[i]; 147 d[ lk[i] ]--; 148 } 149 topu(); 150 for (R i=1;i<=n;++i) 151 { 152 if(v[i]!=1) s[1][i]=i; 153 if(v[i]!=2) s[2][i]=i; 154 } 155 for (R i=2;i<=n;++i) 156 link(i,tf[i]); 157 q=read(); 158 for (R i=1;i<=q;++i) 159 { 160 x=read(); x-=n; a[x]^=1; 161 if(!a[x]) 162 { 163 x=lk[x]; split(1,x); 164 if(!s[2][x]) 165 { 166 splay(x); 167 add(x,-1); 168 } 169 else 170 { 171 x=s[2][x]; splay(x); 172 if(ch[x][1]) add(ch[x][1],-1); 173 v[x]--; update(x); 174 } 175 } 176 else 177 { 178 x=lk[x]; split(1,x); 179 if(!s[1][x]) 180 { 181 splay(x); 182 add(x,1); 183 } 184 else 185 { 186 x=s[1][x]; splay(x); 187 if(ch[x][1]) add(ch[x][1],1); 188 v[x]++; update(x); 189 } 190 } 191 access(1); splay(1); 192 if(v[1]<=1) printf("0 "); 193 else printf("1 "); 194 } 195 return 0; 196 }
由乃的OJ
起床困难综合症上树。这就是一道典型的树剖也可做,只是LCT少一个log的那种题(其实三叉神经树也是)。
起床困难综合症有两种做法,一种是按位贪心,对于每一位跑一遍所有门判断答案;另一种比较技巧,是把111..11,000...00放进去跑一遍,反正每一位是独立的,这样就得到了答案;显然,这道题多组询问,要是对于每一位跑一遍就太太太太太慢了,我们采用第二种方案。LCT上每个点维护111...11,000...00跑一遍后得到的结果,然后用一样的方法按位贪心就好啦!然而,换根的时候,链要进行反转,这些信息不就废了吗?所以,不仅要记录正着跑一遍的信息,也要记录反着跑一遍的信息。这个信息怎么合并呢?假设左儿子+$x$本身跑完后得到的结果是110001001,设为 $a$,那么对于11___1__1这几位,就要取右边全1得到的答案,对于__000_00_,就要取右边全0得到的答案,即$f(x)=(~a&f_1(r)~)|(~(!a)&f_0(r)~)$。这里要格外注意左右儿子的顺序问题,在update的时候,必须保证两个儿子的信息是对的。这很好处理,只要在update以前先pushdown两个儿子就好了。这题在luogu上比较容易通过,但是在bzoj上几乎是必TLE,据说树剖反而可以通过,但是我懒得再写一遍了(毕竟我是在练习LCT),所以还是放一份LCT的代码吧。

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 # define ULL unsigned long long 5 # define getchar() (S==T&&(T=(S=BB)+fread(BB,1,1<<20,stdin),S==T)?EOF:*S++) 6 char BB[1 << 20], *S = BB, *T = BB; 7 8 using namespace std; 9 10 const int N=100005; 11 int n,m,k,x,y; 12 int opt[N],f[N],ch[N][2],rev[N],sta[N]; 13 ULL q,t,v[N],f1[N],f2[N],f3[N],f4[N]; 14 15 void pushdown (int x) 16 { 17 if(!rev[x]) return ; 18 rev[x]=0; swap(ch[x][0],ch[x][1]); 19 if(ch[x][0]) rev[ ch[x][0] ]^=1; 20 if(ch[x][1]) rev[ ch[x][1] ]^=1; 21 swap(f1[x],f3[x]); swap(f2[x],f4[x]); 22 } 23 24 void update (int x) 25 { 26 if(ch[x][0]) pushdown(ch[x][0]); 27 if(ch[x][1]) pushdown(ch[x][1]); 28 int l=ch[x][0],r=ch[x][1]; 29 if(opt[x]==1) 30 { 31 f1[x]=f1[l]&v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]); 32 f2[x]=f2[l]&v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]); 33 f3[x]=f3[r]&v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]); 34 f4[x]=f4[r]&v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]); 35 } 36 else if(opt[x]==2) 37 { 38 f1[x]=f1[l]|v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]); 39 f2[x]=f2[l]|v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]); 40 f3[x]=f3[r]|v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]); 41 f4[x]=f4[r]|v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]); 42 } 43 else 44 { 45 f1[x]=f1[l]^v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]); 46 f2[x]=f2[l]^v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]); 47 f3[x]=f3[r]^v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]); 48 f4[x]=f4[r]^v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]); 49 } 50 } 51 52 inline bool isntroot (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } 53 54 inline int D (int x) { return ch[ f[x] ][1]==x; } 55 56 inline void rotate (int x) 57 { 58 int F=f[x],g=f[F]; 59 int dx=D(x),df=D(F); 60 int k=ch[x][dx^1]; 61 ch[F][dx]=k; ch[x][dx^1]=F; 62 if(ch[g][df]==F) ch[g][df]=x; 63 if(k) f[k]=F; f[F]=x; f[x]=g; 64 update(F); update(x); 65 } 66 67 inline void splay (int x) 68 { 69 int y=x,tp=0; sta[++tp]=x; 70 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 71 for (R i=tp;i>=1;--i) pushdown(sta[i]); 72 while(isntroot(x)) 73 { 74 int t=f[x]; 75 if(!isntroot(t)) rotate(x); 76 else if(D(t)==D(x)) rotate(t),rotate(x); 77 else rotate(x),rotate(x); 78 } 79 } 80 81 inline ULL solve (int x,ULL v) 82 { 83 ULL ans=0,s=0; 84 for (R i=k-1;i>=0;--i) 85 { 86 ULL ans1=(1ull<<i)&f1[x],ans2=(1ull<<i)&f2[x]; 87 if(s+(1ull<<i)>v) { ans+=ans2; continue; } 88 if(ans1>ans2) ans+=ans1,s+=(1ull<<i); 89 else ans+=ans2; 90 } 91 return ans; 92 } 93 94 void access (int x) 95 { 96 int y=0; 97 while(1) 98 { 99 splay(x); ch[x][1]=y; 100 update(x); 101 y=x; x=f[x]; 102 if(!x) return; 103 } 104 } 105 106 void makeroot (int x) { access(x); splay(x); rev[x]^=1; } 107 108 void split (int x,int y) { makeroot(x); access(y); splay(x); } 109 110 void link (int x,int y) { makeroot(x); f[x]=y; } 111 112 int read1() 113 { 114 int x=0; 115 char c=getchar(); 116 while (!isdigit(c)) c=getchar(); 117 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 118 return x; 119 } 120 121 ULL read2() 122 { 123 ULL x=0; 124 char c=getchar(); 125 while (!isdigit(c)) c=getchar(); 126 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 127 return x; 128 } 129 130 int firs[N],h,dep[N]; 131 struct edge { int too,nex; }g[N<<1]; 132 133 void add (int x,int y) 134 { 135 g[++h].nex=firs[x]; 136 firs[x]=h; 137 g[h].too=y; 138 } 139 140 void dfs (int x) 141 { 142 int j; 143 for (R i=firs[x];i;i=g[i].nex) 144 { 145 j=g[i].too; 146 if(dep[j]) continue; 147 dep[j]=1; f[j]=x; 148 dfs(j); 149 } 150 } 151 152 int main() 153 { 154 n=read1(); m=read1(); k=read1(); 155 for (R i=1;i<=n;++i) 156 opt[i]=read1(),v[i]=read2(); 157 for (R i=0;i<k;++i) q+=(1ull<<i); 158 f1[0]=q; f3[0]=q; 159 for (R i=1;i<=n;++i) 160 { 161 if(opt[i]==1) f1[i]=q&v[i],f2[i]=0,f3[i]=q&v[i],f4[i]=0; 162 else if(opt[i]==2) f1[i]=q,f2[i]=v[i],f3[i]=q,f4[i]=v[i]; 163 else f1[i]=q^v[i],f2[i]=v[i],f3[i]=q^v[i],f4[i]=v[i]; 164 } 165 for (R i=2;i<=n;++i) 166 { 167 x=read1(); y=read1(); 168 add(x,y); add(y,x); 169 } 170 dep[1]=1; dfs(1); 171 for (R i=1;i<=m;++i) 172 { 173 int o; 174 o=read1(); x=read1(); y=read1(); t=read2(); 175 if(o==1) 176 { 177 split(x,y); 178 printf("%llu ",solve(x,t)); 179 } 180 else 181 { 182 access(x); splay(x); 183 opt[x]=y; v[x]=t; 184 update(x); 185 } 186 } 187 return 0; 188 }
维护生成树的LCT
大多数维护生成树的题首先都是以维护边权为基础的。LCT还可以维护边权嘛?化边为点就好啦。要么支持加边,要么支持删边(时间倒流),总之不能两者都支持,因为删边时可能会引起一系列以前加边时删掉的边重新被选中,那就根本没法做了。
魔法森林
题意概述:一张无向图中,每条边有两个属性$(a,b)$,要求找到一条 $1$ 到 $n$ 的路径,使得 $max(a)+max(b)$ 最小;$n<=50000,m<=100000$;
看上去有点难?两个参数互相影响,怎么处理才好呢?对于这种题目,我们常常采用固定一维信息的方法;
考虑枚举 $max(a)$,将 $leq max(a)$ 的边加进去,求一个关于 $b$ 的最小生成树,就可以得到答案了。这样的复杂度是 $m^2log m$ 的,过于不科学;
显然,随着枚举的那个 $max(a)$ 的增加,能用来构建最小生成树的边是越来越多的,也就是说...只有加边,没有删边?明示LCT维护关于b的最小生成树,这道题就做完了;
一点小细节:LCT的点数应为n+m,真·点的点权设为-inf,以防止被错误的当成路径最大值删掉。

1 # include <cstdio> 2 # include <iostream> 3 # include <algorithm> 4 # define R register int 5 6 using namespace std; 7 8 const int M=200005; 9 const int inf=1000000000; 10 int n,m,f[M],ch[M][2],rev[M],v[M],id[M],sta[M],s[M]; 11 struct edge { int x,y,a,b; }e[M]; 12 13 bool cmp (edge a,edge b) { return a.a<b.a; } 14 15 void update (int x) 16 { 17 v[x]=s[x]; id[x]=x; 18 if(v[ ch[x][0] ]>v[x]) v[x]=v[ ch[x][0] ],id[x]=id[ ch[x][0] ]; 19 if(v[ ch[x][1] ]>v[x]) v[x]=v[ ch[x][1] ],id[x]=id[ ch[x][1] ]; 20 } 21 22 bool isntroot (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } 23 24 int D (int x) { return (ch[ f[x] ][1]==x); } 25 26 void rotate (int x) 27 { 28 int F=f[x],g=f[F]; 29 int dx=D(x),df=D(F); 30 int k=ch[x][dx^1]; 31 ch[F][dx]=k; ch[x][dx^1]=F; 32 if(ch[g][df]==F) ch[g][df]=x; 33 if(k) f[k]=F; f[F]=x; f[x]=g; 34 update(F); update(x); 35 } 36 37 void pushdown (int x) 38 { 39 if(!rev[x]) return; 40 rev[x]=0; swap(ch[x][0],ch[x][1]); 41 if(ch[x][0]) rev[ ch[x][0] ]^=1; 42 if(ch[x][1]) rev[ ch[x][1] ]^=1; 43 } 44 45 void splay (int x) 46 { 47 int y=x,tp=0; sta[++tp]=x; 48 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 49 for (R i=tp;i>=1;--i) pushdown(sta[i]); 50 while(isntroot(x)) 51 { 52 int t=f[x]; 53 if(!isntroot(t)) rotate(x); 54 else if(D(t)==D(x)) rotate(t),rotate(x); 55 else rotate(x),rotate(x); 56 } 57 } 58 59 void access (int x) 60 { 61 int y=0; 62 while(1) 63 { 64 splay(x); ch[x][1]=y; 65 update(x); 66 y=x; x=f[x]; 67 if(!x) return; 68 } 69 } 70 71 void makeroot (int x) 72 { 73 access(x); splay(x); 74 rev[x]^=1; 75 } 76 77 void split (int x,int y) { makeroot(x); access(y); splay(y); } 78 79 void link (int x,int y) { makeroot(x); f[x]=y; } 80 81 void cut (int x,int y) 82 { 83 split(x,y); 84 ch[y][0]=f[x]=0; 85 update(y); 86 } 87 88 int findroot (int x) 89 { 90 access(x); splay(x); pushdown(x); 91 while(ch[x][0]) x=ch[x][0],pushdown(x); 92 splay(x); 93 return x; 94 } 95 96 int main() 97 { 98 scanf("%d%d",&n,&m); 99 for (R i=1;i<=m;++i) 100 scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].a,&e[i].b); 101 sort(e+1,e+1+m,cmp); 102 int ans=inf; 103 for (R i=1;i<=n;++i) v[i]=-inf,id[i]=i,s[i]=-inf; 104 for (R i=1;i<=m;++i) v[i+n]=e[i].b,id[i+n]=i+n,s[i+n]=e[i].b; 105 for (R i=1;i<=m;++i) 106 { 107 int x=e[i].x,y=e[i].y; 108 if(findroot(x)==findroot(y)) 109 { 110 split(x,y); 111 if(v[y]>e[i].b) 112 { 113 int t=id[y]; 114 cut(t,e[ t-n ].x),cut(t,e[ t-n ].y),link(x,i+n),link(i+n,y); 115 } 116 }else link(x,i+n),link(i+n,y); 117 if(findroot(1)==findroot(n)) 118 { 119 split(1,n); 120 ans=min(ans,e[i].a+v[n]); 121 } 122 } 123 if(ans==inf) printf("-1"); 124 else printf("%d",ans); 125 return 0; 126 }
水管局长
这道题就是删边啦,把它倒过来,转变为加边就好了;这里有一个小细节(指bzoj加强版):整个过程中删去的边并不多,所以最后留下的边很多,用LCT来处理这部分很容易就TLE了。那怎么办呢?Kruscal求最小生成树,求完后再用LCT把它建出来就好啦!虽然LCT的理论复杂度是 $nlog n$,但实际上1e6跑起来就很费劲了,所以,还是多想想有没有哪些部分是可以优化的吧。

1 # include <cstdio> 2 # include <iostream> 3 # include <map> 4 # include <algorithm> 5 # define R register int 6 # define getchar() (S==T&&(T=(S=BB)+fread(BB,1,1<<20,stdin),S==T)?EOF:*S++) 7 char BB[1 << 20], *S = BB, *T = BB; 8 9 using namespace std; 10 11 const int N=1200006; 12 const int Q=100005; 13 const int inf=1000000000; 14 int n,m,q,x[N],y[N],t[N],vis[N],opt[Q],a[Q],b[Q]; 15 int f[N],ch[N][2],s[N],v[N],id[N],rev[N],sta[N]; 16 int ans[Q]; 17 map < pair<int,int>,int > M; 18 19 void update (int x) 20 { 21 v[x]=s[x]; id[x]=x; 22 if(v[ ch[x][0] ]>v[x]) v[x]=v[ ch[x][0] ],id[x]=id[ ch[x][0] ]; 23 if(v[ ch[x][1] ]>v[x]) v[x]=v[ ch[x][1] ],id[x]=id[ ch[x][1] ]; 24 } 25 26 bool isntroot (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } 27 28 int D (int x) { return (ch[ f[x] ][1]==x); } 29 30 void rotate (int x) 31 { 32 int F=f[x],g=f[F]; 33 int dx=D(x),df=D(F); 34 int k=ch[x][dx^1]; 35 ch[F][dx]=k; ch[x][dx^1]=F; 36 if(ch[g][df]==F) ch[g][df]=x; 37 if(k) f[k]=F; f[F]=x; f[x]=g; 38 update(F); update(x); 39 } 40 41 void pushdown (int x) 42 { 43 if(!rev[x]) return; 44 rev[x]=0; swap(ch[x][0],ch[x][1]); 45 if(ch[x][0]) rev[ ch[x][0] ]^=1; 46 if(ch[x][1]) rev[ ch[x][1] ]^=1; 47 } 48 49 void splay (int x) 50 { 51 int y=x,tp=0; sta[++tp]=x; 52 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 53 for (R i=tp;i>=1;--i) pushdown(sta[i]); 54 while(isntroot(x)) 55 { 56 int t=f[x]; 57 if(!isntroot(t)) rotate(x); 58 else if(D(t)==D(x)) rotate(t),rotate(x); 59 else rotate(x),rotate(x); 60 } 61 } 62 63 void access (int x) 64 { 65 int y=0; 66 while(1) 67 { 68 splay(x); ch[x][1]=y; 69 update(x); 70 y=x; x=f[x]; 71 if(!x) return; 72 } 73 } 74 75 void makeroot (int x) 76 { 77 access(x); splay(x); 78 rev[x]^=1; 79 } 80 81 void split (int x,int y) { makeroot(x); access(y); splay(y); } 82 83 void link (int x,int y) { makeroot(x); f[x]=y; } 84 85 void cut (int x,int y) 86 { 87 split(x,y); 88 ch[y][0]=f[x]=0; 89 update(y); 90 } 91 92 int findroot (int x) 93 { 94 access(x); splay(x); pushdown(x); 95 while(ch[x][0]) x=ch[x][0],pushdown(x); 96 splay(x); 97 return x; 98 } 99 100 void ins (int i) 101 { 102 split(x[i],y[i]); 103 if(v[ y[i] ]<=t[i]) return; 104 int pos=id[ y[i] ]; 105 cut(pos,x[pos-n]); cut(pos,y[pos-n]); 106 link(i+n,x[i]); link(i+n,y[i]); 107 } 108 109 int read() 110 { 111 int x=0; 112 char c=getchar(); 113 while (!isdigit(c)) c=getchar(); 114 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 115 return x; 116 } 117 118 struct edge { int x,y,z,id; }e[N]; 119 int tf[N],eh; 120 121 int fa (int x) 122 { 123 if(tf[x]==x) return x; 124 return tf[x]=fa(tf[x]); 125 } 126 127 bool cmp (edge a,edge b) { return a.z<b.z; } 128 129 void kruscal() 130 { 131 for (R i=1;i<=n+m;++i) tf[i]=i; 132 sort(e+1,e+1+eh,cmp); 133 for (R i=1;i<=eh;++i) 134 { 135 int x=e[i].x,y=e[i].y; 136 x=fa(x); y=fa(y); 137 if(x==y) continue; 138 tf[x]=y; 139 link(e[i].id+n,e[i].x); 140 link(e[i].id+n,e[i].y); 141 } 142 } 143 144 int main() 145 { 146 n=read(),m=read(),q=read(); 147 v[0]=s[0]=-inf; 148 for (R i=1;i<=n;++i) 149 v[i]=-inf,s[i]=-inf,id[i]=i; 150 for (R i=1;i<=m;++i) 151 { 152 x[i]=read(); y[i]=read(); t[i]=read(); 153 v[i+n]=t[i]; s[i+n]=t[i]; id[i+n]=i+n; 154 if(x[i]>y[i]) swap(x[i],y[i]); 155 M[ make_pair(x[i],y[i]) ]=i; 156 } 157 for (R i=1;i<=q;++i) 158 { 159 opt[i]=read(); a[i]=read(); b[i]=read(); 160 if(a[i]>b[i]) swap(a[i],b[i]); 161 if(opt[i]==1) continue; 162 vis[ M[ make_pair(a[i],b[i]) ] ]=1; 163 } 164 for (R i=1;i<=m;++i) 165 if(!vis[i]) 166 { 167 eh++; 168 e[eh].x=x[i]; e[eh].y=y[i]; e[eh].z=t[i]; 169 e[eh].id=i; 170 } 171 kruscal(); 172 for (R i=q;i>=1;--i) 173 { 174 if(opt[i]==1) 175 { 176 split(a[i],b[i]); 177 ans[i]=v[ b[i] ]; 178 } 179 else 180 ins(M[ make_pair(a[i],b[i]) ]); 181 } 182 for (R i=1;i<=q;++i) 183 if(opt[i]==1) printf("%d ",ans[i]); 184 return 0; 185 }
最小差值生成树
好了好了,我知道我很水,几乎一样的题做三遍,但是这回我是用虚拟机里的emacs写的这道题,所以也有一定意义啦~
没什么好说的,枚举最大值,成环的时候删最小值就好了。
一点小细节:如何求当前LCT中最小边的编号?开一个桶,记录每条边是否存在,因为随着边的增加,最小边的编号单调不减,可以用一个指针维护;

1 # include <cstdio> 2 # include <iostream> 3 # include <algorithm> 4 # define R register int 5 6 using namespace std; 7 8 const int N=300005; 9 const int inf=1000000000; 10 int n,m,it[N],ed; 11 int f[N],ch[N][2],v[N],s[N],id[N],rev[N],tf[N]; 12 int sta[N]; 13 struct edge { int x,y,z; }e[N]; 14 15 bool isntroot (int x) { return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); } 16 17 int D (int x) { return ch[ f[x] ][1]==x; } 18 19 void update (int x) 20 { 21 id[x]=x; s[x]=v[x]; 22 if(s[ ch[x][0] ]<s[x]) 23 s[x]=s[ ch[x][0] ],id[x]=id[ ch[x][0] ]; 24 if(s[ ch[x][1] ]<s[x]) 25 s[x]=s[ ch[x][1] ],id[x]=id[ ch[x][1] ]; 26 } 27 28 void pushdown (int x) 29 { 30 if(!rev[x]) return; rev[x]=0; 31 if(ch[x][0]) rev[ ch[x][0] ]^=1; 32 if(ch[x][1]) rev[ ch[x][1] ]^=1; 33 swap(ch[x][0],ch[x][1]); 34 } 35 36 void rotate (int x) 37 { 38 int F=f[x],g=f[F]; 39 int dx=D(x),df=D(F); 40 int k=ch[x][dx^1]; 41 ch[x][dx^1]=F; ch[F][dx]=k; 42 if(ch[g][df]==F) ch[g][df]=x; 43 if(k) f[k]=F; f[F]=x; f[x]=g; 44 update(F); update(x); 45 } 46 47 void splay (int x) 48 { 49 int y=x,tp=0; sta[++tp]=x; 50 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 51 for (R i=tp;i>=1;--i) pushdown(sta[i]); 52 while(isntroot(x)) 53 { 54 int t=f[x]; 55 if(!isntroot(t)) rotate(x); 56 else if(D(x)==D(t)) rotate(t),rotate(x); 57 else rotate(x),rotate(x); 58 } 59 } 60 61 void access (int x) 62 { 63 int y=0; 64 while(1) 65 { 66 splay(x); ch[x][1]=y; 67 update(x); 68 y=x; x=f[x]; 69 if(!x) return; 70 } 71 } 72 73 void makeroot (int x) 74 { 75 access(x); splay(x); 76 rev[x]^=1; 77 } 78 79 void split (int x,int y) 80 { 81 makeroot(x); access(y); splay(y); 82 } 83 84 void link (int x,int y) 85 { 86 makeroot(x); f[x]=y; 87 } 88 89 void cut (int x,int y) 90 { 91 split(x,y); 92 ch[y][0]=f[x]=0; 93 update(y); 94 } 95 96 bool cmp (edge a,edge b) { return a.z<b.z; } 97 98 int fa (int x) 99 { 100 if(x==tf[x]) return x; 101 return tf[x]=fa(tf[x]); 102 } 103 104 int main() 105 { 106 scanf("%d%d",&n,&m); 107 v[0]=s[0]=inf; 108 for (R i=1;i<=n;++i) 109 v[i]=inf,id[i]=i,s[i]=inf; 110 for (R i=1;i<=m;++i) 111 scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z); 112 sort(e+1,e+1+m,cmp); 113 for (R i=1;i<=m;++i) v[i+n]=s[i+n]=e[i].z,id[i+n]=i+n; 114 int mp=n+1,ans=inf; 115 for (R i=1;i<=n;++i) tf[i]=i; 116 for (R i=1;i<=m;++i) 117 { 118 int x=e[i].x,y=e[i].y; 119 if(x==y) continue; 120 if(fa(x)==fa(y)) 121 { 122 split(x,y); 123 int pos=id[y]; it[pos]=0; 124 cut(pos,e[pos-n].x); cut(pos,e[pos-n].y); 125 link(i+n,x); link(i+n,y); 126 it[i+n]=1; 127 } 128 else link(i+n,x),link(i+n,y),it[i+n]=1,ed++,tf[ fa(x) ]=fa(y); 129 while(it[mp]==0) mp++; 130 if(ed==n-1) ans=min(ans,e[i].z-e[mp-n].z); 131 } 132 printf("%d",ans); 133 return 0; 134 }
维护子树信息的LCT
LCT更擅长做一些关于树链的问题,但是呢...毒瘤出题人总能想办法将数据结构的功能扩展再扩展,所以就有了维护子树信息的LCT。
其实,LCT维护子树听起来奥妙重重,写起来却没多难;首先,子树=实子树+虚子树;是否可以考虑对于每个点维护它的虚子树信息呢?其实是可以哒。下面将以维护子树大小为例讲讲这种LCT,$si[x]$ 表示的是x所有虚子树的大小的和;
首先是update:

access:
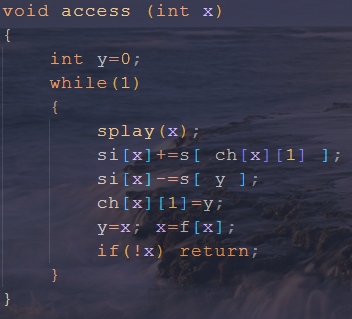
link:

然后就没了...因为子树信息只有在新加儿子或者切换虚实儿子的时候才会有影响,在别的时候根本不用改动;
大融合
掌握了LCT维护子树信息的方法,这道题就很简单啦。
首先我们都知道,这个边的“负载”指的就是(n-x到y方向的子树大小)*(n-y到x方向的子树大小);不过这样有一点点麻烦,可以考虑转化,先 $split(x,y)$,然后答案就是(y的虚子树和+1)*(x的虚子树和+1)啦;画个图方便理解:
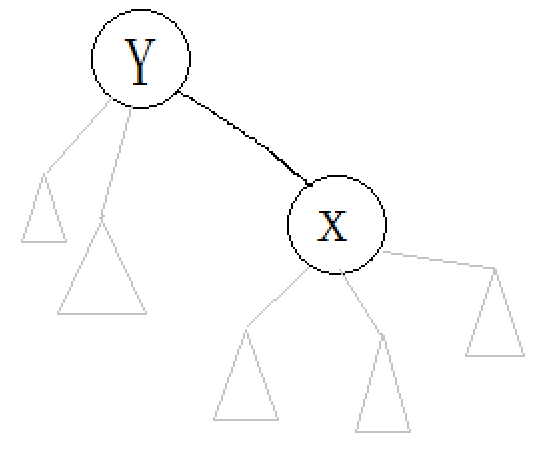

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define ll long long 5 # define R register int 6 7 using namespace std; 8 9 const int N=100005; 10 int n,q,x,y; 11 int f[N],ch[N][2],s[N],si[N],rev[N],sta[N]; 12 char st[5]; 13 14 bool isntroot (int x) 15 { 16 return (ch[ f[x] ][0]==x||ch[ f[x] ][1]==x); 17 } 18 19 void pushdown (int x) 20 { 21 if(!rev[x]) return; rev[x]=0; 22 if(ch[x][0]) rev[ ch[x][0] ]^=1; 23 if(ch[x][1]) rev[ ch[x][1] ]^=1; 24 swap(ch[x][0],ch[x][1]); 25 } 26 27 int D (int x) 28 { 29 return ch[ f[x] ][1]==x; 30 } 31 32 void update (int x) 33 { 34 s[x]=si[x]+s[ ch[x][0] ]+s[ ch[x][1] ]+1; 35 } 36 37 void rotate (int x) 38 { 39 int F=f[x],g=f[F]; 40 int dx=D(x),df=D(F); 41 int k=ch[x][dx^1]; 42 ch[x][dx^1]=F; ch[F][dx]=k; 43 if(ch[g][df]==F) ch[g][df]=x; 44 if(k) f[k]=F; f[F]=x; f[x]=g; 45 update(F); update(x); 46 } 47 48 void splay (int x) 49 { 50 int tp=0,y=x; sta[++tp]=x; 51 while(isntroot(y)) sta[++tp]=f[y],y=f[y]; 52 for (R i=tp;i>=1;--i) pushdown(sta[i]); 53 while(isntroot(x)) 54 { 55 int t=f[x]; 56 if(!isntroot(t)) rotate(x); 57 else if(D(t)==D(x)) rotate(t),rotate(x); 58 else rotate(x),rotate(x); 59 } 60 } 61 62 void access (int x) 63 { 64 int y=0; 65 while(1) 66 { 67 splay(x); 68 si[x]+=s[ ch[x][1] ]; 69 si[x]-=s[ y ]; 70 ch[x][1]=y; 71 y=x; x=f[x]; 72 if(!x) return; 73 } 74 } 75 76 void makeroot (int x) 77 { 78 access(x); splay(x); 79 rev[x]^=1; 80 } 81 82 void link (int x,int y) 83 { 84 makeroot(x); access(y); splay(y); 85 f[x]=y; si[y]+=s[x]; s[y]+=s[x]; 86 } 87 88 ll ask (int x,int y) 89 { 90 makeroot(x); access(y); splay(y); 91 return 1LL*(si[y]+1)*s[x]; 92 } 93 94 int main() 95 { 96 scanf("%d%d",&n,&q); 97 for (R i=1;i<=n;++i) s[i]=1; 98 for (R i=1;i<=q;++i) 99 { 100 scanf("%s",st+1); 101 scanf("%d%d",&x,&y); 102 if(st[1]=='A') 103 link(x,y); 104 else 105 printf("%lld ",ask(x,y)); 106 } 107 return 0; 108 }
首都
一道很神神神神神神的题!
题意概述:维护一个森林,要求支持动态加边,问某个点目前所在联通块的重心,
