关于查找,让我们分类别讨论:
如果面对一组无序的数据,可以考虑用顺序查找,时间复杂度为O(N)。
如果面对一组有序的数据,则可以考虑用折半查找,时间复杂度为O(lgN)。
如果面对的有序数据较大,则需要分段折半查找。
如果面对一组无序且较大的数据,此时则要求先排序,再查找。这里就可以利用我们的二叉搜索树。
一.插入数据。
让我们看下面这组数组:array[10]={5,3,4,1,7,8,2,6,0,9}。
我们可以根据以下规则制造一棵二叉搜索树:
1.如果数据进来是空树,则确定该数据为树的根。
2.如果数据进来时树已经有了根,则根据“值大向右,值小向左,值等退出”的规则,知道遇到一片指向空的区域,生成一个新的节点。
根据规则,我们由数组array得到如下二叉搜索树:

关键代码有其二:
1.生成新结点的代码:
pNode pNew = (pNode)malloc(sizeof(Node)); //判断开辟空间是否成功? if (pNew == NULL) { printf("malloc failed! "); return NULL; } //初始化 pNew->data_ = data; pNew->left_ = NULL; pNew->right_ = NULL;
2.插入数据的代码(这里注意要分开讨论):
!!!注意,代码勿忘对二级指针断言判空!!!
情况1:数据插入时是空树。
if (*pRoot == NULL) { *pRoot = BuyBSTreeNode(data); }
情况2:数据插入时是非空。
//prev用于保存双亲 pNode pCur = *pRoot; pNode prev = NULL; //找到插入的合适的位置 while (pCur != NULL) { if (data < pCur->data_) { prev = pCur; pCur = pCur->left_; } else if (data > pCur->data_) { prev = pCur; pCur = pCur->right_; } else { printf("BSTree中已有该值。 "); return; } } //进行插入数据步骤 if (data < prev->data_) { pCur = BuyBSTreeNode(data); prev->left_ = pCur; } else if (data > prev->data_) { pCur = BuyBSTreeNode(data); prev->right_ = pCur; return 1; }
二.查找数据。
如今已经完成了构建二叉搜索树,那么下一步就是查找对应的值。
二叉搜索树查找和折半查找类似,不同的是折半查找时间复杂度稳定,一定是O(lgN),二叉搜索树要看树的构造,越接近完全二叉树,时间复杂度越接近O(lgN),如果得到的二叉搜索树是一棵单支树,那么时间复杂度则有O(N),那么如何调整一课二叉搜索树呢?我们下篇博客见。
那么既然是查找,就也分两种情况:1.找得到。2.找不到。
找到的标志很简单——所求值和内容值相同。找不到的标志——索引指针标至空区域。
查找的规则和插入几乎一致——“值大往右,值小往左,值等则取值,值空则无”。
//pCur为索引指针 while (pCur != NULL) { if (data < pCur->data_) { pCur = pCur->left_; } else if (data>pCur->data_) { pCur = pCur->right_; } else if (data == pCur->data_) { return pCur; } } return NULL;
三.删除数据
删除数据我们需要分多种情况:
1.需要删除的数据不存在。
2.需要删除的数据为叶子结点。
3.需要删除的数据只有左子树。
4.需要删除的数据只有右子树。
5.需要删除的数据左右子树都存在。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
针对这些情况,我们分类讨论,能合并的尽量合并:
1.如果数据不存在,则直接退出函数,因为无法删除指定数据,这也包括树是空树的情况。
2.如果找到需要删除的数据,发现其为叶子节点,则直接让其双亲本来指向它的指针,改为指向NULL。
3.如果找到需要删除的数据,发现其只有左子树,则直接让其双亲本来指向它的指针,改为指向其左子树,这里我们可以看出来,其实2中指向NULL,等同于指向叶子节点的左子树。
4.如果找到需要删除的数据,发现其只有右子树,则直接让其双亲本来指向它的指针,改为指向其右子树。
5.如果找到需要删除的数据,发现其左右子树均存在,则找到上述3或4情况下的结点且满足“一定条件”代替它,然后删除用来替代的结点。
(“一定条件”:这个结点可以是大于该结点的最小结点,也可以是小于该节点的最大结点。)
(此处我们选择用情况4的结点代替情况5的结点,方式是该节点右子树中最左边的结点。)
(例如:如果我们要删 7 ,则用8来代替7的位置,然后本来的8。)
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
所以我们经过总结,得到如下图四种情况:
1.原图中删10:(未找到)

//////////没找到的情况 //pCur为索引指针 if (pCur == NULL) { printf("The %d is not in BSTree. ", data); return 0; }
2.原图中删2(叶子结点)

3.后续-图中删1(只有左子树)

//prev是标识双亲的指针,pCur为索引指针,下同 if (NULL == pCur->right_) { pDel = pCur; //小情况1:所删节点为根,且根无右子树 if (pCur == (*pRoot)) { *pRoot = pCur->left_; } //小情况2:所删节点非根 else { //要分pDel是prev左或右子树的情况。(这个需要if else) if (prev->left_ == pDel) { prev->left_ = pDel->left_; } else if (prev->right_ == pDel) { prev->right_ = pDel->left_; } } }
4.原图中删9(只有右子树)
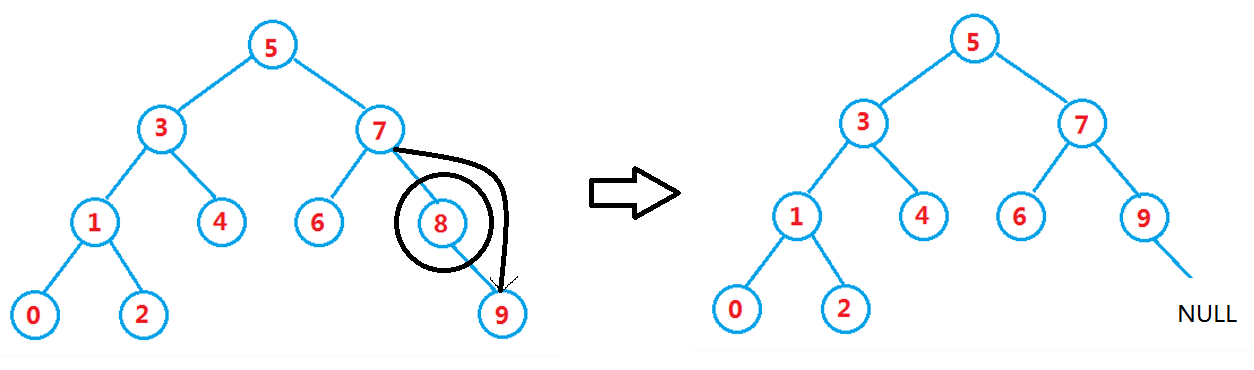
//2.只有右孩子 else if (NULL == pCur->left_) { pDel = pCur; //小情况1:所删节点为根,且根无右子树(大情况1里有包含) /*if (pCur == *pRoot) { *pRoot = pCur->left_; }*/ //小情况2:所删节点非根 //要分pDel是prev左或右子树的情况。(这个需要if else) if (prev->left_ == pDel) { prev->left_ = pDel->right_; } else if (prev->right_ == pDel) { prev->right_ = pDel->right_; } }
5.原图中删7(左右孩子都存在)
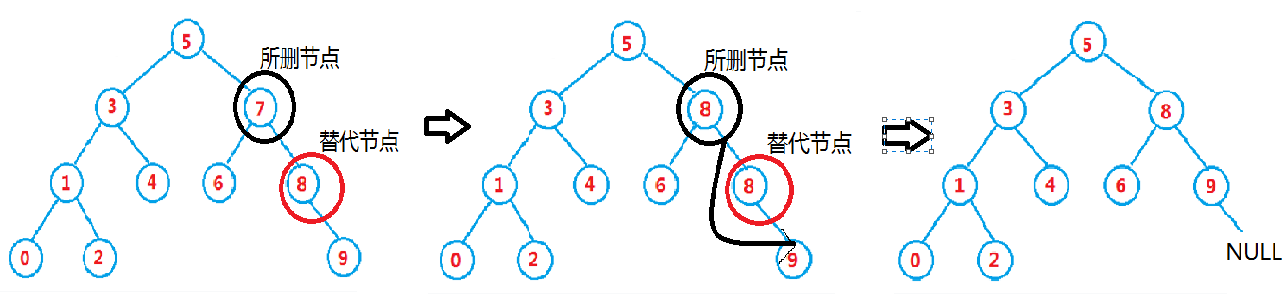
//找到需要和当前节点交换值得前两张情况的结点。 //需要更新双亲(万一循环进不去) prev = pCur; pDel = pCur->right_; while (pDel->left_) { prev = pDel; pDel = pDel->left_; } //把值带进去 pCur->data_ = pDel->data_; //此时pDel可以确定是没有左子树的 //---要分pDel有无右子树(其实就算右子树是NULL也是直接接)---没有分情况的必要 //和pDel是prev左或右子树的情况。(这个需要if else) if (prev->left_ == pDel) { prev->left_ = pDel->right_; } else if (prev->right_ == pDel) { prev->right_ = pDel->right_; }
6.在代码中可以看到。其中一种情况,是所删的数据为根,且根只有左子树。如图。

比如我要删二叉搜索树中的5,那很简单,我直接让根结点指向3即可(同样,如果所删为根且根只有右子树,做相应考虑)。
所以!!!很重要的一点,因为可能会要改变根的指向,所以函数中要传二级指针。
综上,为二叉搜索树复习一。
拓展:递归实现插入,查找,删除。