队列的一个使用场景
银行排队的案例:
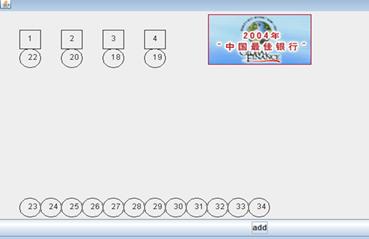
队列介绍
-
队列是一个有序列表,可以用数组或是链表来实现。
-
遵循先入先出的原则。即:先存入队列的数据,要先取出。后存入的要后取出
-
示意图:(使用数组模拟队列示意图)
数组模拟队列
-
队列本身是有序列表,若使用数组的结构来存储队列的数据,则队列数组的声明如下其中 maxSize 是该队列的最大容量。
-
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量 front(head)及 rear(tail)分别记录队列前后端的下标,front 会随着数据输出而改变,而 rear则是随着数据输入而改变,如图所示:
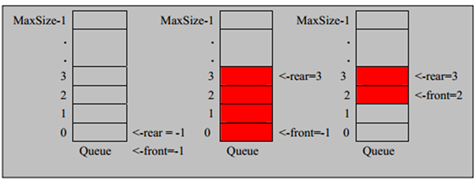
说明

代码实现
package com.atguigu.chapter18
import scala.io.StdIn
object ArrayQueueDemo {
def main(args: Array[String]): Unit = {
//初始化一个队列
val queue = new ArrayQueue(3)
var key = ""
while (true) {
println("show: 表示显示队列")
println("exit: 表示退出程序")
println("add: 表示添加队列数据")
println("get: 表示取出队列数据")
println("head: 查看队列头的数据(不改变队列)")
key = StdIn.readLine()
key match {
case "show" => queue.showQueue()
case "add" => {
println("请输入一个数")
val value = StdIn.readInt()
queue.addQueue(value)
}
case "get" => {
val res = queue.getQueue()
if (res.isInstanceOf[Exception]) {
println(res.asInstanceOf[Exception].getMessage)
} else {
println(s"取出数据是 $res")
}
}
case "head" => {
val res = queue.headQueue()
if(res.isInstanceOf[Exception]) {
//显示错误信息
println(res.asInstanceOf[Exception].getMessage)
}else {
println("队列头元素值为=" + res)
}
}
case "exit" => System.exit(0)
}
}
}
}
//使用数组模拟队列
//队列存在的问题是,数据空间不能复用
class ArrayQueue(arrMaxSize: Int) {
val maxSize = arrMaxSize
val arr = new Array[Int](maxSize) //该数组存放数据,模拟队列
var front = -1 // 指向队列头部, 分析出front 是指向队列数据的前一个位置
var rear = -1 // 指向队列的尾部,分析出rear 是指向队列的最后数据(含)
//判断队列是否满
def isFull(): Boolean = {
rear == maxSize - 1
}
//判断队列是否空
def isEmpty(): Boolean = {
front == rear
}
//添加数据到队列
def addQueue(n: Int): Unit = {
//判断是否满
if (isFull()) {
println("队列满,无法加入..")
return
}
rear += 1 //先让rear 后移
arr(rear) = n
}
def getQueue(): Any = {
if (isEmpty()) {
return new Exception("队列空~")
}
front += 1
return arr(front)
}
//显示队列的所有数据
def showQueue(): Unit = {
if (isEmpty()) {
println("队列空的,没有数据..")
return
}
for (i <- front + 1 to rear) {
printf("arr[%d]=%d ", i, arr(i))
}
}
//查看队列的头元素,但是不是改变队列
def headQueue(): Any = {
if (isEmpty()) {
return new Exception("队列空~")
}
//这里注意,不要去改变fornt 值
return arr(front + 1)
}
}
对上面代码的说明: 虽然实现了队列,但是数据空间不能复用,因此我们需要对其进行优化,使用取模的方式实现环形队列.
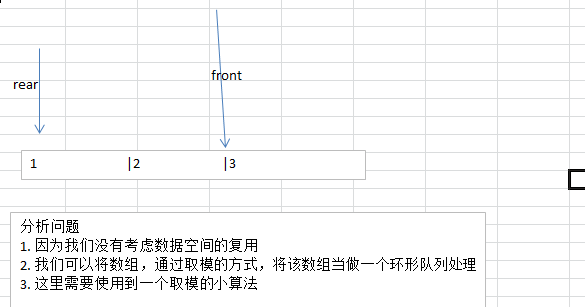
数组模拟环形队列
-
对前面的数组模拟队列的优化,充分利用数组. 因此将数组看做是一个环形的。(通过取模的方
式来实现即可)因为数组也可以通过取模的方式当做一个环形结构来使用,那么也可以解决约瑟夫问题.(提示,可以通过修改元素的值,来标志该元素对应的小孩是否出圈)
-
分析说明:
-
尾索引的下一个为头索引时表示队列满,即将队列容量空出一个作为约定,这个在做判断队列满的
时候需要注意 (rear + 1) % maxSize == front 满] -
rear == front [空]
-
代码实现
package com.atguigu.chapter18
import scala.io.StdIn
object CircleArrayQueueDemo {
def main(args: Array[String]): Unit = {
println("~~~环形队列的案例~~~")
//初始化一个队列
val queue = new CircleArrayQueue(4)
var key = ""
while (true) {
println("show: 表示显示队列")
println("exit: 表示退出程序")
println("add: 表示添加队列数据")
println("get: 表示取出队列数据")
println("head: 查看队列头的数据(不改变队列)")
key = StdIn.readLine()
key match {
case "show" => queue.showQueue()
case "add" => {
println("请输入一个数")
val value = StdIn.readInt()
queue.addQueue(value)
}
case "get" => {
val res = queue.getQueue()
if (res.isInstanceOf[Exception]) {
println(res.asInstanceOf[Exception].getMessage)
} else {
println(s"取出数据是 $res")
}
}
case "head" => {
val res = queue.headQueue()
if(res.isInstanceOf[Exception]) {
//显示错误信息
println(res.asInstanceOf[Exception].getMessage)
}else {
println("队列头元素值为=" + res)
}
}
case "exit" => System.exit(0)
}
}
}
}
//环形的队列和前面的单向队列有类似的地方,因为我们修改即可
class CircleArrayQueue(arrMaxSize: Int) {
val maxSize = arrMaxSize
val arr = new Array[Int](maxSize) //该数组存放数据,模拟队列
var front = 0 // 指向队列头部
var rear = 0 // 指向队列的尾部
//判断队列满的方法
//队列容量空出一个作为约定
def isFull(): Boolean = {
//1 => rear 1
//2 => rear 2
//3 => rear 3
(rear + 1) % maxSize == front
}
//判断队列空的条件
def isEmpty(): Boolean = {
rear == front
}
//添加数据到队列
def addQueue(n: Int): Unit = {
//判断是否满
if (isFull()) {
println("队列满,无法加入..")
return
}
//将数据加入
arr(rear) = n
//然后将rear 后移, 这里必须考虑取模
rear = (rear + 1) % maxSize
}
//取出队列的数据(按先进先出的原则)
def getQueue(): Any = {
if (isEmpty()) {
return new Exception("队列空~")
}
//这里我们需要分析处理 front 已经指向了队列的头元素
//1. 先把front 对应的数据保存到变量
//2. 将front后移
//3. 返回前面保存的变量值
val value = arr(front)
front = (front + 1) % maxSize
return value
}
//显示队列的所有数据
def showQueue(): Unit = {
if (isEmpty()) {
println("队列空的,没有数据..")
return
}
//思路: 从front 取,取出几个元素
//动脑筋
for (i <- front until front + size()) {
printf("arr[%d]=%d ", i % maxSize, arr(i % maxSize))
}
}
//求出当前环形队列有几个元素
//动脑筋
//基础【问题/需求 ---> 设计算法】
def size(): Int = {
//rear = 1
//front = 0
//maxSize = 3
(rear + maxSize - front) % maxSize //求出当前队列实际有多少个数据
}
//查看队列的头元素,但是不是改变队列
def headQueue(): Any = {
if (isEmpty()) {
return new Exception("队列空~")
}
//这里注意,不要去改变fornt 值
return arr(front)
}
}
课堂练习:
-
同学们完成环形数组模拟的队列的输出
(cq.tail + cq.maxSize - cq.head) % cq.maxSize