排序的介绍
排序是将一组数据,依指定的顺序进行排列的过程, 常见的排序:
-
冒泡排序
-
选择排序
-
插入排序
-
快速排序
-
归并排序
冒泡排序
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从后向前(从下标较大的元素开始),依次比较
相邻元素的排序码,若发现逆序则交换,使排序码较小的元素逐渐从后部移向前部(从下标较大的单元移向下
标较小的单元),就象水底下的气泡一样逐渐向上冒。
因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下
来没有进行过交换,就说明序列有序,因此要在排序过程中设置
一个标志flag判断元素是否进行过交换。从而减少不必要的比较。
冒泡排序,前面的老师,已经讲过了。
-
冒泡排序的代码:
|
package com.atguigu.temp.sort import java.text.SimpleDateFormat import java.util.Date object BubbleSort { def main(args: Array[String]): Unit = { //数组 //val arr = Array(3, 9, -1, 10, 20) //创建一个80000个随机数据的数组 val random = new util.Random() val arr = new Array[Int](80000) for (i <- 0 until 80000) { arr(i) = random.nextInt(8000000) } println("排序前") val now: Date = new Date() val dateFormat: SimpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss") val date = dateFormat.format(now) println("排序前时间=" + date) //输出时间
println(arr.mkString(" ")) println("排序后") bubbleSort(arr) println(arr.mkString(" ")) val now2: Date = new Date() val date2 = dateFormat.format(now2) println("排序后时间=" + date2) //输出时间 } def bubbleSort(arr: Array[Int]): Unit = {
for (i <- 0 until arr.length - 1) { for (j <- 0 until arr.length - 1 - i) { if (arr(j) > arr(j + 1)) { val temp = arr(j) arr(j) = arr(j + 1) arr(j + 1) = temp } } } } } |
选择排序基本介绍
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,经过和其他元素重整,再依规定()交换位置后达到排序的目的。
选择排序思想:
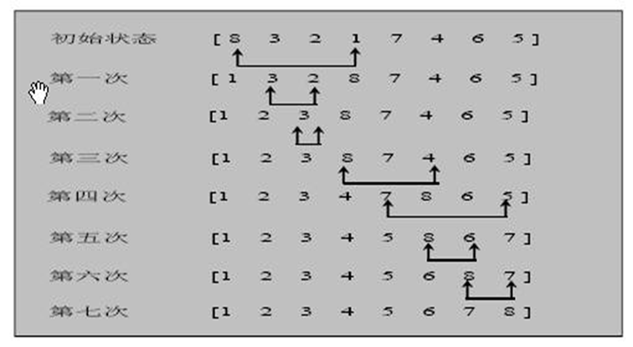
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从R[0]~R[n-1]中选取最小值,与R[0]交换,第二次从R[1]~R[n-1]中选取最小值,与R[1]交换,第三次从R[2]~R[n-1]中选取最小值,与R[2]交换,…,第i次从R[i-1]~R[n-1]中选取最小值,与R[i-1]交换,…, 第n-1次从R[n-2]~R[n-1]中选取最小值,与R[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
选择排序思路分析图:
选择排序的代码实现
|
package com.atguigu.chapter18.sort
import java.text.SimpleDateFormat import java.util.Date
object SelectSort { def main(args: Array[String]): Unit = { //var arr = Array(101, 34, 119, 1)
val random = new util.Random() val arr = new Array[Int](80000) for (i <- 0 until 80000) { //循环的生成随机数 arr(i) = random.nextInt(8000000) } println("排序前") val now: Date = new Date() val dateFormat: SimpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss") val date = dateFormat.format(now) println("排序前时间=" + date) //输出时间
//我们发现规律,调用选择排序 selectSort(arr)
println("排序后") //println(arr.mkString(" ")) val now2: Date = new Date() val date2 = dateFormat.format(now2) println("排序后时间=" + date2) //输出时间
//我们看一下排序的一个演变过程 //第1轮排序 (101, 34, 119, 1) => (1, 34, 119, 101)
/*
var min = arr(0) var minIndex = 0 //遍历 for (j <- (0 + 1) until arr.length) { if (min > arr(j)) { // 说明min不是真的最小值 min = arr(j) // 重置min minIndex = j // 重置minIndex } } //判断是否需要交换 if (minIndex != 0) { arr(minIndex) = arr(0) arr(0) = min }
println("第1轮结束") println(arr.mkString(" "))
//第2轮排序 (1, 34, 119, 101) => (1, 34, 119, 101)
min = arr(1) minIndex = 1 //遍历 for (j <- (1 + 1) until arr.length) { if (min > arr(j)) { // 说明min不是真的最小值 min = arr(j) // 重置min minIndex = j // 重置minIndex } } //判断是否需要交换 if (minIndex != 1) { arr(minIndex) = arr(1) arr(1) = min }
println("第2轮结束") println(arr.mkString(" "))
//第3轮排序 (1, 34, 119, 101) => (1, 34, 101, 119)
min = arr(2) minIndex = 2 //遍历 for (j <- (2 + 1) until arr.length) { if (min > arr(j)) { // 说明min不是真的最小值 min = arr(j) // 重置min minIndex = j // 重置minIndex } } //判断是否需要交换 if (minIndex != 2) { arr(minIndex) = arr(2) arr(2) = min }
println("第3轮结束") println(arr.mkString(" ")) */
}
def selectSort(arr:Array[Int]): Unit = {
for (i <- 0 until arr.length -1) { var min = arr(i) var minIndex = i //遍历 for (j <- (i + 1) until arr.length) { if (min > arr(j)) { // 说明min不是真的最小值 min = arr(j) // 重置min minIndex = j // 重置minIndex } } //判断是否需要交换 if (minIndex != i) { arr(minIndex) = arr(i) arr(i) = min }
// println(s"第${i+1}轮结束") // println(arr.mkString(" ")) } } } |
插入排序法介绍:
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
插入排序法思想:
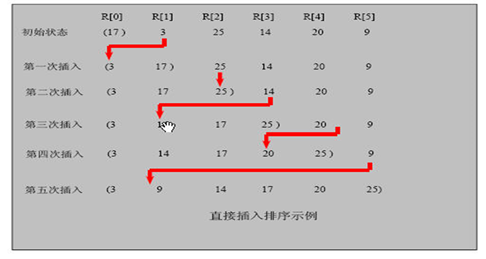
插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
插入排序法思路示意图
插入排序的代码实现
|
package com.atguigu.chapter18.sort
import java.text.SimpleDateFormat import java.util.Date
object InsertSort { def main(args: Array[String]): Unit = {
//测试数组 //val arr = Array(101, 34, 119, 1,-1, 45,900)
val random = new util.Random() val arr = new Array[Int](80000) for (i <- 0 until 80000) { //循环的生成随机数 arr(i) = random.nextInt(8000000) } println("排序前") val now: Date = new Date() val dateFormat: SimpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss") val date = dateFormat.format(now) println("排序前时间=" + date) //输出时间
insertSort(arr) //调用插入排序
println("插入排序后")
val now2: Date = new Date() val date2 = dateFormat.format(now2) println("排序后时间=" + date2) //输出时间 //println(arr.mkString(" "))
//第1轮插入排序 //(101), 34, 119, 1 => (34,101),119,1
// (101, 101) 119, 1 /* var insertVal = arr(1) var insertIndex = 1 - 1 // 表示有序表的最后这个元素的下标
//还没找到位置 while (insertIndex >= 0 && insertVal < arr(insertIndex)) { arr(insertIndex+1) = arr(insertIndex) insertIndex -= 1 } //退出while 说明插入的位置就找到了 arr(insertIndex + 1) = insertVal
println("第1轮的结果是") println(arr.mkString(" "))
//第2轮 insertVal = arr(2) insertIndex = 2 - 1 // 表示有序表的最后这个元素的下标
//还没找到位置 while (insertIndex >= 0 && insertVal < arr(insertIndex)) { arr(insertIndex+1) = arr(insertIndex) insertIndex -= 1 } //退出while 说明插入的位置就找到了 arr(insertIndex + 1) = insertVal
println("第2的结果是") println(arr.mkString(" "))
//第3轮 insertVal = arr(3) insertIndex = 3 - 1 // 表示有序表的最后这个元素的下标
//还没找到位置 while (insertIndex >= 0 && insertVal < arr(insertIndex)) { arr(insertIndex+1) = arr(insertIndex) insertIndex -= 1 } //退出while 说明插入的位置就找到了 arr(insertIndex + 1) = insertVal
println("第3的结果是") println(arr.mkString(" "))*/
}
def insertSort(arr:Array[Int]): Unit ={ //发现规律 for (i <- 1 until arr.length) { var insertVal = arr(i) var insertIndex = i - 1 // 表示有序表的最后这个元素的下标
//还没找到位置 while (insertIndex >= 0 && insertVal < arr(insertIndex)) { arr(insertIndex+1) = arr(insertIndex) insertIndex -= 1 } //退出while 说明插入的位置就找到了 arr(insertIndex + 1) = insertVal
// println(s"第${i}轮的结果是") // println(arr.mkString(" ")) } } }
/* 插入排序的思路: 插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
*/ |
快速排序(Quicksort)是对冒泡排序的一种改进。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
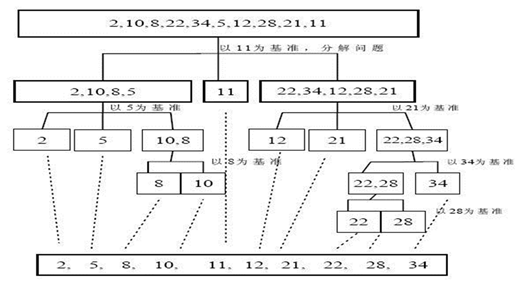
- 代码实现
|
package com.atguigu.chapter18.sort
import java.text.SimpleDateFormat import java.util.Date
import util.control.Breaks._
object QuickSort { def main(args: Array[String]): Unit = {
//val arr = Array(-9,78,0,23,-567,70)
val random = new util.Random() val arr = new Array[Int](80000000) for (i <- 0 until 80000000) { //循环的生成随机数 arr(i) = random.nextInt(8000000) } println("排序前") val now: Date = new Date() val dateFormat: SimpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss") val date = dateFormat.format(now) println("排序前时间=" + date) //输出时间
quickSort(0, arr.length -1, arr) // 调用快排 println("排序后")
val now2: Date = new Date() val date2 = dateFormat.format(now2) println("排序后时间=" + date2) //输出时间 //println(arr.mkString(" ")) // ( 0 )// -567 -9 0 23 78 70 }
/* 1. left: 指定从数组的左边的下标 0 2. right : 指定从数组的右边的下标 length -1 3. arr : 进行排序的数组 */ def quickSort(left: Int, right: Int, arr: Array[Int]): Unit = { var l = left // 左下标 var r = right // 右下标 var pivot = arr((left + right) / 2) // 以中间的值为基准进行分割 var temp = 0 breakable { // while 语句的作用就是把比 pivot 小的数放到左边, 比pivot大的数放到右边 while (l < r) { while (arr(l) < pivot) { //从左边找一个比 pivot 大的值对应下标 l += 1 } while (arr(r) > pivot) { //从右边找一个比 pivot 小的值对应下标 r -= 1 } if (l >= r) { // 说明本次交换结束,退出本次while break() } var temp = arr(l) //交换 arr(l) = arr(r) arr(r) = temp //处理后,如果发现arr(l) == pivot 就r - =1 , 提高效率 if (arr(l) == pivot) { r -= 1 } // if ((arr(r)) == pivot) { l += 1 } } } if (l == r) { // 提高效率 l += 1 r -= 1 }
if (left < r) { //向左递归排序 quickSort(left, r, arr) } if (right > l) {//向右递归排序 quickSort(l, right, arr) } }
} |
归并排序介绍:
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
归并排序思想示意图1-基本思想:
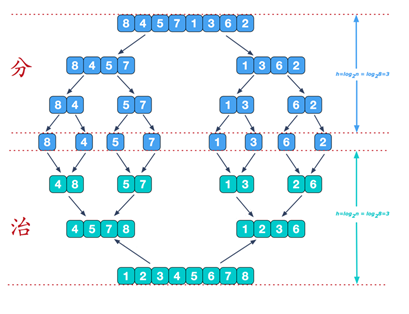
归并排序思想示意图2-合并相邻有序子序列:
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤
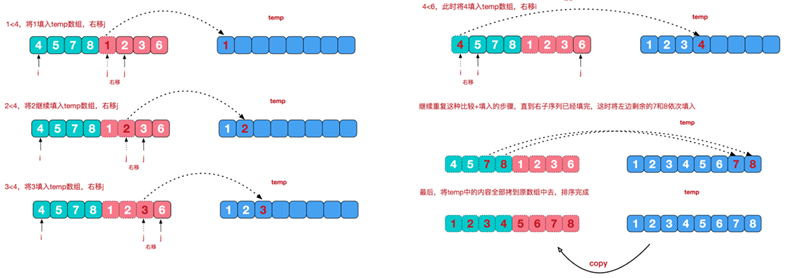
- 归并排序的代码实现
|
package com.atguigu.chapter18.sort
import java.text.SimpleDateFormat import java.util.Date
object MergeSort { def main(args: Array[String]): Unit = {
//var arr = Array(-9, 78, 0, 23, -567, 70)
val random = new util.Random() val arr = new Array[Int](80000000) for (i <- 0 until 80000000) { //循环的生成随机数 arr(i) = random.nextInt(8000000) } println("排序前") val now: Date = new Date() val dateFormat: SimpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss") val date = dateFormat.format(now)
val temp = new Array[Int](arr.length) //临时的数组
println("排序前时间=" + date) //输出时间
mergeSort(arr, 0, arr.length - 1, temp) //调用归并排序法
println("归并排序后")
val now2: Date = new Date() val date2 = dateFormat.format(now2) println("排序后时间=" + date2) //输出时间
// println(arr.mkString(" "))
}
//是后一个归并排序 /* 1. arr :待排序的数组 2. left: 最初的左边的下标 0 3. right: 最初的右边下标 length - 1 4. temp :就是临时数组 , 事先就开辟好的,大小和 arr 一样. */ def mergeSort(arr: Array[Int], left: Int, right: Int, temp: Array[Int]): Unit = { if (left < right) { //如果 left < right 就可以继续分 val mid = (left + right) / 2 mergeSort(arr, left, mid, temp) // 递归将左边的数据做成有序列表 mergeSort(arr, mid + 1, right, temp) //递归将右边的数据做成有序列表 // merge 是合并的操作 merge(arr, left, mid, right, temp) } }
def merge(arr: Array[Int], left: Int, mid: Int, right: Int, temp: Array[Int]) { var i = left // i 就是左边指针[索引] var j = mid + 1 //j 就是右边的指针 var t = 0 // t 是temp 数组的索引 while (i <= mid && j <= right) { // 如果是当前的左边的有序列表的值小于当前的右边有序列表的值 // 就把这个值拷贝到 temp数组 if (arr(i) <= arr(j)) { temp(t) = arr(i) t += 1 i += 1 } else { // 如果是当前的右边的有序列表的值小于当前的左边有序列表的值,就把这个值拷贝到 temp数组 temp(t) = arr(j) t += 1 j += 1 } } while (i <= mid) { //如果左边有序列表还有剩余数据,就依次拷贝到temp数组 temp(t) = arr(i) t += 1 i += 1 } while (j <= right) { //如果右边有序列表还有剩余数据,就依次拷贝到temp数组 temp(t) = arr(j) t += 1 j += 1 }
// 下面代码是完成将本次的temp 的数据拷贝到arr中 t = 0 var tempLeft = left while (tempLeft <= right) { arr(tempLeft) = temp(t) t += 1 tempLeft += 1 } }
} |
课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000.
-
新版的代码如下
|
package com.atguigu.chapter18.search
import scala.collection.mutable.ArrayBuffer import util.control.Breaks._
object BinarySearch { def main(args: Array[String]): Unit = {
val arr = Array(1, 8, 10, 1000, 1000,1000, 1000, 1000, 1000,1000, 1000,1000, 1234) // val index = binarySearch(arr, 0, arr.length - 1, 1000) // if (index != -1) { // println("找到,下标为" + index) // } else { // println("没有找到") // }
var resArr = binarySearch2(arr, 0, arr.length - 1, 1000) resArr = resArr.sortBy((x:Int) => x) if (resArr.length != 0) { for (index<-resArr) { println("找到的索引有" + index) } }else { println("没有找到") } }
//二分查找的思路 //1. 先找到中间值 //2. 然后将中间值和查找值比较 //2.1 相等,找出 //2.2 中间值 > 查找值, 向左进行递归查找 //2.3 中间值 < 查找值, 向右进行递归查找 // ? 在什么情况下,表示找不到? //如果存在值,就返回对应的下标,否则返回-1 def binarySearch(arr: Array[Int], l: Int, r: Int, findVal: Int): Int = {
//找不到条件? if (l > r) { return -1 }
val midIndex = (l + r) / 2 val midVal = arr(midIndex) if (midVal > findVal) { //向左进行递归查找 binarySearch(arr, l, midIndex - 1, findVal) } else if (midVal < findVal) { //向右进行递归查找 binarySearch(arr, midIndex + 1, r, findVal) } else { return midIndex }
}
/* 课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000. //分析 1. 返回的结果是一个可变数组 ArrayBuffer 2. 在找到结果时,向左边扫描,向右边扫描 [条件] 3. 找到结果后,就加入到ArrayBuffer */ def binarySearch2(arr: Array[Int], l: Int, r: Int, findVal: Int): ArrayBuffer[Int] = {
//找不到条件? if (l > r) { return ArrayBuffer() }
val midIndex = (l + r) / 2 val midVal = arr(midIndex) if (midVal > findVal) { //向左进行递归查找 binarySearch2(arr, l, midIndex - 1, findVal) } else if (midVal < findVal) { //向右进行递归查找 binarySearch2(arr, midIndex + 1, r, findVal) } else { println("midIndex=" + midIndex) //定义一个可变数组 val resArr = ArrayBuffer[Int]() //向左边扫描 var temp = midIndex - 1 breakable { while (true) { if (temp < 0 || arr(temp) != findVal) { break() } if (arr(temp) == findVal) { resArr.append(temp) } temp -= 1 } } //将中间这个索引加入 resArr.append(midIndex) //向右边扫描 temp = midIndex + 1 breakable { while (true) { if (temp > arr.length - 1 || arr(temp) != findVal) { break() } if (arr(temp) == findVal) { resArr.append(temp) } temp += 1 } } return resArr }
} } |