[学习电子教案](https://2d.hep.com.cn/1865445/9)
科学计算可视化
分类
信息可视化(信息、知识)
科学可视化(空间数据)
主要方法
二维标量数据场
颜色映射法
等值线法
立体图法
层次分割法
三维标量数据场
面绘制法
体绘制法
矢量数据场
直接法
用箭头、线段、色轮等手段表示矢量数据
流线法
应用领域

- 科学计算的基本概念
- numpy库的使用
- matplotlib库的使用
**一、科学计算的基本概念:**
科学计算需要采用矩阵运算库numpy和绘制库matplotlib
**二、numpy库的使用:**
1、numpy库概述:

**数据类型**:处理基础数据类型为同种元素构成的多维数组(ndarray)。
**索引**:数组中元素可用整数索引,序号从零开始。
**维度,轴,秩**:ndarray类型的维度(dimensions)叫做轴(axes),轴的个数叫做秩(rank)一维数组秩为1,以此类推。
**引用**:
`import numpy as np`
2、numpy库解析
1)numpy常用的数组(ndarray类型)创建函数(7个)
| 函数| 描述|
|--|--|
| np.array([x,y,z],dtype=int) |从Python列表和元组创造数组 |
| np.arange(x,y,i)| 创建一个从x到y,步长为 i 的数组|
| np.linspace(x,y,n)|创建一个从x到y,等分成 n 个元素的数组 |
|np.indices((m,n))|创建一个 m 行 n 列的矩阵|
|np.random.rand(m,n)|创建一个 m 行 n 列的随机数组|
|np.ones((m,n),dtype)|创建一个 m 行 n 列全为 1 的数组,dtype是数据类型|
|np.empty((m,n),dtype)|创建一个 m 行 n 列全为0的数组,dtype是数据类型|
2)
3、示例:图像的手绘效果
1)图像的数组表示:
图像是有规则的二维数组,可以用numpy将图像转换成数组对象:
1 #e17.1HandDrawPic.py 2 from PIL import Image 3 import numpy as np 4 vec_el = np.pi/2.2 # 光源的俯视角度,弧度值 5 vec_az = np.pi/4. # 光源的方位角度,弧度值 6 depth = 10. # (0-100) 7 im = Image.open('fcity.jpg').convert('L') 8 a = np.asarray(im).astype('float') 9 grad = np.gradient(a) #取图像灰度的梯度值 10 grad_x, grad_y = grad #分别取横纵图像梯度值 11 grad_x = grad_x*depth/100. 12 grad_y = grad_y*depth/100. 13 dx = np.cos(vec_el)*np.cos(vec_az) #光源对x 轴的影响 14 dy = np.cos(vec_el)*np.sin(vec_az) #光源对y 轴的影响 15 dz = np.sin(vec_el) #光源对z 轴的影响 16 A = np.sqrt(grad_x**2 + grad_y**2 + 1.) 17 uni_x = grad_x/A 18 uni_y = grad_y/A 19 uni_z = 1./A 20 a2 = 255*(dx*uni_x + dy*uni_y + dz*uni_z) #光源归一化 21 a2 = a2.clip(0,255) 22 im2 = Image.fromarray(a2.astype('uint8')) #重构图像 23 im2.save('fcityHandDraw.jpg')

三、matplotlib库的使用

实例1:基本三角函数图像实现
1 import numpy as np 2 import matplotlib.pyplot as plt 3 x = np.linspace(0, 6, 100) 4 y = np.cos(2 * np.pi * x) * np.exp(-x)+0.8 5 plt.plot(x, y, 'k', color='r', linewidth=3, linestyle="-") 6 plt.show()
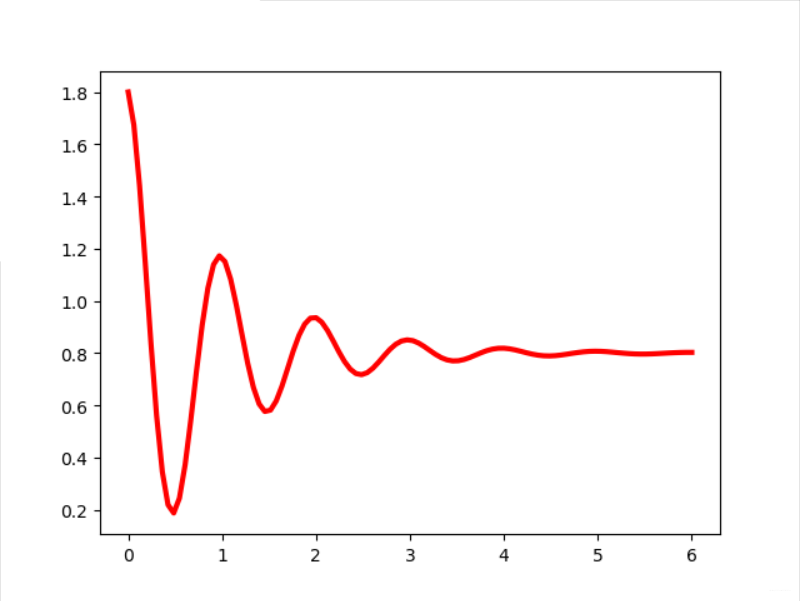
实例2:带标识的坐标系
1 import matplotlib.pyplot as plt 2 import matplotlib 3 matplotlib.rcParams['font.family']='SimHei' 4 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] 5 plt.plot([1,2,4], [1,2,3]) 6 plt.title("坐标系标题") 7 plt.xlabel('时间 (s)') 8 plt.ylabel('范围 (m)') 9 plt.xticks([1,2,3,4,5],[r'$pi/3$', r'$2pi/3$', r'$pi$', 10 r'$4pi/3$', r'$5pi/3$'])
11 plt.show()
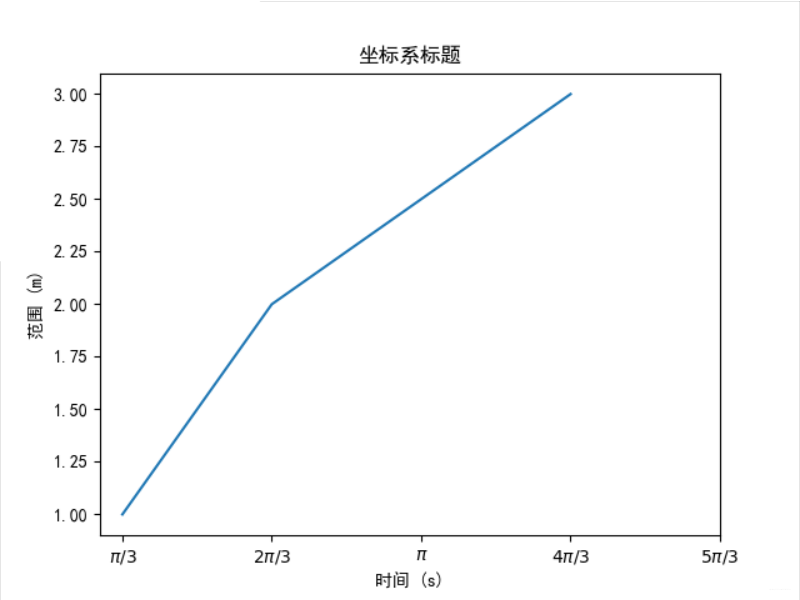
实例3:带阴影的坐标系
1 import matplotlib.pyplot as plt 2 import numpy as np 3 x = np.linspace(0, 10, 1000) 4 y = np.cos(2*np.pi*x) * np.exp(-x)+0.8 5 plt.plot(x,y,'k',color='r',label="$exp-decay$",linewidth=3) 6 plt.axis([0,6,0,1.8]) 7 ix = (x>0.8) & (x<3) 8 plt.fill_between(x, y ,0, where = ix, 9 facecolor='grey', alpha=0.25) 10 plt.text(0.5*(0.8+3), 0.2, r"$int_a^b f(x)mathrm{d}x$", 11 horizontalalignment='center') 12 plt.legend() 13 plt.show()
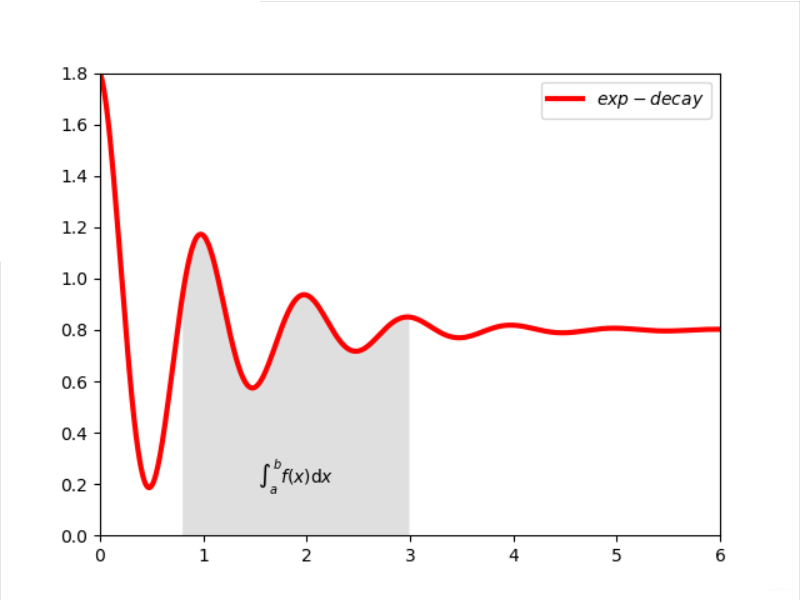
实例4:带阻尼衰减曲线坐标图绘制
1 ##e18.1PlotDamping.py 2 import numpy as np 3 import matplotlib.pyplot as plt 4 import matplotlib 5 matplotlib.rcParams['font.family']='SimHei' 6 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] 7 def Draw(pcolor, nt_point, nt_text, nt_size): 8 plt.plot(x, y, 'k', label="$exp_decay$", color=pcolor, linewidth=3, linestyle="-") 9 plt.plot(x, z, "b--", label="$cos(x^2)$", linewidth=1) 10 plt.xlabel('时间(s)') 11 plt.ylabel('幅度(mV)') 12 plt.title("阻尼衰减曲线绘制") 13 plt.annotate('$cos(2 pi t) exp(-t)$', xy=nt_point, xytext=nt_text, fontsize=nt_size, 14 arrowprops=dict(arrowstyle='->', connectionstyle="arc3,rad=.1")) 15 def Shadow(a, b): 16 ix = (x>a) & (x<b) 17 plt.fill_between(x,y,0,where=ix,facecolor='grey', alpha=0.25) 18 plt.text(0.5 * (a + b), 0.2, "$int_a^b f(x)mathrm{d}x$", 19 horizontalalignment='center') 20 def XY_Axis(x_start, x_end, y_start, y_end): 21 plt.xlim(x_start, x_end) 22 plt.ylim(y_start, y_end) 23 plt.xticks([np.pi/3, 2 * np.pi/3, 1 * np.pi, 4 * np.pi/3, 5 * np.pi/3], 24 ['$pi/3$', '$2pi/3$', '$pi$', '$4pi/3$', '$5pi/3$']) 25 x = np.linspace(0.0, 6.0, 100) 26 y = np.cos(2 * np.pi * x) * np.exp(-x)+0.8 27 z = 0.5 * np.cos(x ** 2)+0.8 28 note_point,note_text,note_size = (1, np.cos(2 * np.pi) * np.exp(-1)+0.8),(1, 1.4), 14 29 fig = plt.figure(figsize=(8, 6), facecolor="white") 30 plt.subplot(111) 31 Draw("red", note_point, note_text, note_size) 32 XY_Axis(0, 5, 0, 1.8) 33 Shadow(0.8, 3) 34 plt.legend() 35 plt.savefig('sample.JPG') 36 plt.show()
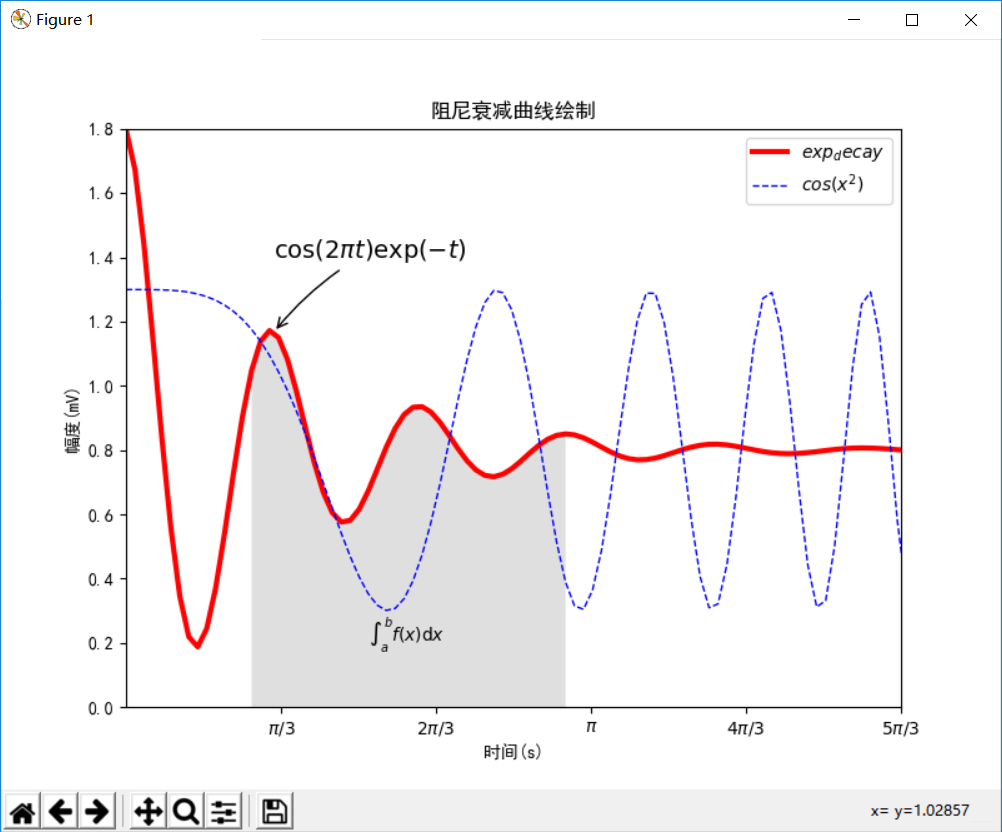
实例5:多级雷达图绘制
DOTA人物能力值雷达图绘制
1 #e19.1DrawRadar 2 import numpy as np 3 import matplotlib.pyplot as plt 4 import matplotlib 5 matplotlib.rcParams['font.family']='SimHei' 6 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] 7 labels = np.array(['综合', 'KDA', '发育', '推进', '生存','输出']) 8 nAttr = 6 9 data = np.array([7, 5, 6, 9, 8, 7]) #数据值 10 angles = np.linspace(0, 2*np.pi, nAttr, endpoint=False) 11 data = np.concatenate((data, [data[0]])) 12 angles = np.concatenate((angles, [angles[0]])) 13 fig = plt.figure(facecolor="white") 14 plt.subplot(111, polar=True) 15 plt.plot(angles,data,'bo-',color ='g',linewidth=2) 16 plt.fill(angles,data,facecolor='g',alpha=0.25) 17 plt.thetagrids(angles*180/np.pi, labels) 18 plt.figtext(0.52, 0.95, 'DOTA能力值雷达图', ha='center') 19 plt.grid(True) 20 plt.show()

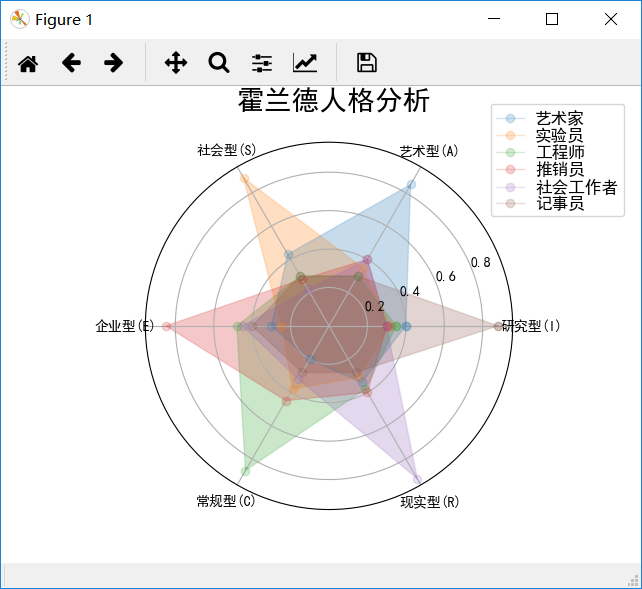
实例6:霍兰德人格分析雷达图绘制
1 #HollandRadarDraw.py 2 from numpy import array,shape,arange 3 import numpy as np 4 import matplotlib.pyplot as plt 5 import matplotlib 6 matplotlib.rcParams['font.family']='SimHei' 7 radar_labels = np.array(['研究型(I)','艺术型(A)','社会型(S)', 8 '企业型(E)','常规型(C)','现实型(R)']) #雷达标签 9 nAttr = 6 10 data = np.array([[0.40, 0.32, 0.35, 0.30, 0.30, 0.88], 11 [0.85, 0.35, 0.30, 0.40, 0.40, 0.30], 12 [0.43, 0.89, 0.30, 0.28, 0.22, 0.30], 13 [0.30, 0.25, 0.48, 0.85, 0.45, 0.40], 14 [0.20, 0.38, 0.87, 0.45, 0.32, 0.28], 15 [0.34, 0.31, 0.38, 0.40, 0.92, 0.28]]) #数据值 16 data_labels = ('艺术家', '实验员', '工程师', '推销员', '社会工作者','记事员') 17 angles = np.linspace(0, 2*np.pi, nAttr, endpoint=False) 18 data = np.concatenate((data, [data[0]])) 19 angles = np.concatenate((angles, [angles[0]])) 20 fig = plt.figure(facecolor="white") 21 plt.subplot(111, polar=True) 22 plt.plot(angles,data,'o-', linewidth=1, alpha=0.2) 23 plt.fill(angles,data, alpha=0.25) 24 plt.thetagrids(angles*180/np.pi, radar_labels) 25 plt.figtext(0.52, 0.95, '霍兰德人格分析', ha='center', size=20) 26 legend = plt.legend(data_labels, loc=(0.94, 0.80), labelspacing=0.1) 27 plt.setp(legend.get_texts(), fontsize='large') 28 plt.grid(True) 29 plt.savefig('holland_radar.jpg')
四、自定义手绘风
1 #e17.1HandDrawPic.py 2 from PIL import Image 3 import numpy as np 4 vec_el = np.pi/2.2 # 光源的俯视角度,弧度值 5 vec_az = np.pi/4. # 光源的方位角度,弧度值 6 depth = 10. # (0-100) 7 im = Image.open('D:\360安全浏览器下载xiaomanyao.jpg').convert('L') 8 a = np.asarray(im).astype('float') 9 grad = np.gradient(a) #取图像灰度的梯度值 10 grad_x, grad_y = grad #分别取横纵图像梯度值 11 grad_x = grad_x*depth/100. 12 grad_y = grad_y*depth/100. 13 dx = np.cos(vec_el)*np.cos(vec_az) #光源对x 轴的影响 14 dy = np.cos(vec_el)*np.sin(vec_az) #光源对y 轴的影响 15 dz = np.sin(vec_el) #光源对z 轴的影响 16 A = np.sqrt(grad_x**2 + grad_y**2 + 1.) 17 uni_x = grad_x/A 18 uni_y = grad_y/A 19 uni_z = 1./A 20 a2 = 255*(dx*uni_x + dy*uni_y + dz*uni_z) #光源归一化 21 a2 = a2.clip(0,255) 22 im2 = Image.fromarray(a2.astype('uint8')) #重构图像 23 im2.save('D:\360安全浏览器下载xaiomanyaoHandDraw.jpg')

**五、模仿实例对自己的成绩进行分析:**
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import matplotlib 4 matplotlib.rcParams['font.family']='SimHei' 5 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] 6 labels = np.array(['第一次', '第二次', '第三次', '第四次', '第五次']) 7 nAttr = 5 8 data = np.array([20,15,17,18,10]) #数据值 9 angles = np.linspace(0, 2*np.pi, nAttr, endpoint=False) 10 data = np.concatenate((data, [data[0]])) 11 angles = np.concatenate((angles, [angles[0]])) 12 fig = plt.figure(facecolor="white") 13 plt.subplot(111, polar=True) 14 plt.plot(angles,data,'bo-',color ='g',linewidth=2) 15 plt.fill(angles,data,facecolor='g',alpha=0.25) 16 plt.thetagrids(angles*180/np.pi, labels) 17 plt.figtext(0.52, 0.95, '舒新城的博客测试分析', ha='center') 18 plt.grid(True) 19 plt.show()

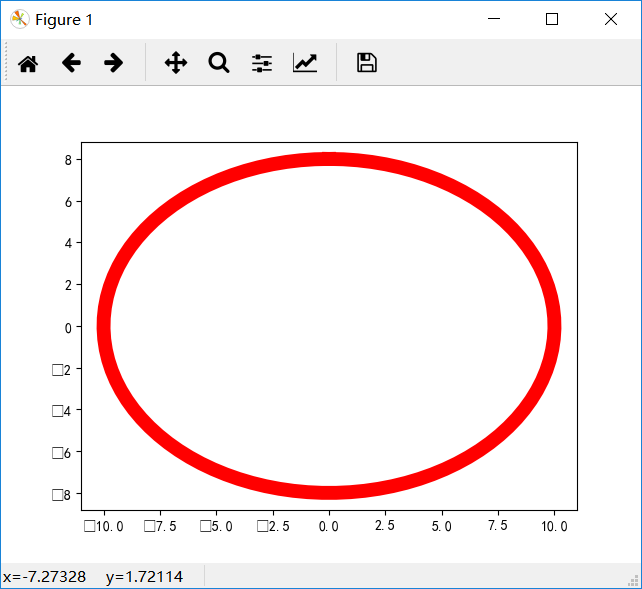
六、绘制一个数学规律图:用极坐标方程绘制圆锥曲线:
1 import numpy as py 2 import matplotlib.pyplot as plt 3 i=np.linspace(0,2*np.pi,100) 4 x=a*np.sin(i) 5 y=b*np.cos(i) 6 plt.plot(x,y,'k',color='r',linewidth='10',linestyle="-") 7 plt.show()
七、运用pandas库处理Excel文件数据