Age of Moyu
题意:
给出n个站点和m条线路(线路即边的权值),每换乘一次线路则钱数+1,问从1到n最少要花多少钱?
分析:
考虑以点建图的话每次转移无法选择哪条线路是最优的(存在多条线路相同的边),因为边具有特殊含义,所以我们就以边建图。定义d【i】为从1点到第i条边的距离,如果边的权值相同则前进一步的代价为0,否则为1,类似dijkstra的思想,不断去松弛其他的边,结果为所有与n相连的边对应d【i】的最小值。
学习博客:大佬博客
代码:

#include <set> #include <queue> #include <vector> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int mod=1e9+7; const int maxn=1e5+100; const int maxm=2e5+100; const int inf=0x3f3f3f3f; int n,m,tot; int d[maxm]; bool done[maxm]; vector<int>vertex[maxm]; struct Edge{ int u,v,c; }; Edge e[maxn<<1]; struct HeapNode { int id,d; HeapNode(int id,int d):id(id),d(d){} bool operator < (const HeapNode& rhs) const { return d > rhs.d; } }; priority_queue<HeapNode>que; void init() { for(int i=1;i<=n;i++){ vertex[i].clear(); } for(int i=1;i<=m;i++){ d[i]=inf; done[i]=false; } while(!que.empty()) que.pop(); } void dijkstra(int s,int t) { while(!que.empty()) { HeapNode x=que.top();que.pop(); int id=x.id; if(done[id]) continue; done[id]=true; int u=e[id].u,v=e[id].v; int lenu=vertex[u].size(); int lenv=vertex[v].size(); for(int i=0;i<lenu;i++){ int eid=vertex[u][i]; int val=!(e[id].c==e[eid].c); if(d[eid]>d[id]+val){ d[eid]=d[id]+val; que.push(HeapNode(eid,d[eid])); } } for(int i=0;i<lenv;i++){ int eid=vertex[v][i]; int val=!(e[id].c==e[eid].c); if(d[eid]>d[id]+val){ d[eid]=d[id]+val; que.push(HeapNode(eid,d[eid])); } } } int ans=inf; int sz=vertex[t].size(); for(int i=0;i<sz;i++){ ans=min(ans,d[vertex[t][i]]); } if(ans==inf) ans=-1; printf("%d ",ans); } int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif while(scanf("%d %d",&n,&m)!=EOF) { init(); for(int i=1;i<=m;i++){ scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].c); if(min(e[i].u,e[i].v)==1){ d[i]=1; que.push(HeapNode(i,d[i])); } vertex[e[i].u].push_back(i); vertex[e[i].v].push_back(i); } dijkstra(1,n); } return 0; }
GuGuFishtion
题意:

 ,给出n,m,p,输出后面式子的值。
,给出n,m,p,输出后面式子的值。
分析:
首先根据欧拉函数的性质phi(n) = (p-1)*p^(α-1)(如果n=p^α),phi(mn)=phi(m)phi(n)(m和n互质),不难得出phi(a)=phi(p1^a1)*phi(p2^a2)……phi(pi^ai),phi(b)=phi(p1'^a1)*phi(p2'^a2)……phi(pj'^ai)(其中pi,pj'为对应a,b质因数分解后的值,ai,bi为每个质因数出现的次数),考虑a*b的质因数分解即为a的质因数分解乘以b的质因数分解,所以对于a,b中独立的质因数(只在a,b的质因数中的一方出现),a*b的质因数分解中也会出现并且幂相同。对于相同的质因数,考虑
a:phi(pi^ai)=(pi-1)*pi^(ai-1)
b:phi(pi^bi)=(pi-1)*pi^(bi-1)
a*b:phi(pi^(ai+bi))=(pi-1)*pi^(ai+bi-1)
分子分母相除后Gu(a,b)=(pi*pj*pk……)/((pi-1) * (pj-1) * (pk-1)……)=(pi*pj*pk……)/(pi*pj*pk * (1-1/pi) * (1-1/pj) * (1-1/pk)……)=gcd(a,b)/phi(gcd(a,b))(其中pi,pj,pk……为a,b中相同的质因数)。
然后问题就可以转化为求,进一步转化为
,对于这个式子就可以枚举k,然后计算(gcd=k的个数)*(k)*(phi(k)的逆元)的累加和就可以了。(其中gcd=k的个数是莫比乌斯的模板题)
参考博客:大佬博客
代码:

#include <queue> #include <vector> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e6+100; int n,m,p,T; bool check[maxn]; int mu[maxn],inv[maxn],phi[maxn],prime[maxn]; void getinv(int n) { inv[1] = 1; for (int i=2; i<=n; ++i) { inv[i] = (ll) (p - p / i) * inv[p%i] % p; } } void geteuler(int n){ phi[1]=1; for(int i=2;i<=n;i++) phi[i]=i; for(int i=2;i<=n;i++) if(phi[i]==i) for(int j=i;j<=n;j+=i) phi[j]=phi[j]/i*(i-1); } void Moblus(int n) { mu[1]=1; int tot=0; cls(check); for(int i=2;i<=n;i++){ if(!check[i]){ prime[tot++]=i; mu[i]=-1; } for(int j=0;j<tot;j++){ if(i*prime[j]>n) break; check[i*prime[j]]=true; if(i%prime[j]==0){ mu[i*prime[j]]=0; break; } else { mu[i*prime[j]]=-mu[i]; } } } } ll calc(int n,int m,int k) { if(k==0) return 0; ll ans=0; n/=k;m/=k; if(n>m) swap(n,m); for(int i=1;i<=n;i++){ ans=(ans+(ll)mu[i]*(n/i)*(m/i))%p; } return ans; } int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif // ONLINE_JUDGE Moblus(maxn-1); geteuler(maxn-1); scanf("%d",&T); for(int kase=1;kase<=T;kase++){ scanf("%d %d %d",&n,&m,&p); ll ans=0; getinv(maxn-1); for(int i=1;i<=min(n,m);i++){ ans=(ans+calc(n,m,i)*i%p*inv[phi[i]]%p)%p; } printf("%lld ",ans); } return 0; }
Traffic Network in Numazu
题意:
给出n个点n条边,2种操作(修改第u条边的权值为v,求u到v之间的最短路)
分析:
这题有两种解法(树链剖分+线段树,lca+树状数组),大佬口中的模板题……
整体思想就是把树上的点通过dfs序或者欧拉序变成一段区间,通过线段树(树状数组)维护区间和。
代码:
树链剖分+线段树

#include <map> #include <queue> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e5+100; int tot; int n,q,T; bool vis[maxn]; int W[maxn],head[maxn]; struct E{ int u,v,w; }; E e[maxn<<1]; struct Edge { int v,nex; }; Edge edge[maxn<<1]; void addEdge(int u,int v) { edge[tot].v=v; edge[tot].nex=head[u]; head[u]=tot++; } void init() { tot=0; cls(vis); clslow(head); } namespace IntervalTree { #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 ll add[maxn<<2],sum[maxn<<2]; void PushUp(int rt) { sum[rt]=sum[rt<<1]+sum[rt<<1|1]; } void PushDown(int m,int rt) { if(add[rt]){ add[rt<<1]=add[rt<<1|1]=add[rt]; sum[rt<<1]=(m-(m>>1))*add[rt]; sum[rt<<1|1]=(m>>1)*add[rt]; add[rt]=0; } } void build(int l,int r,int rt) { add[rt]=0; if(l==r){ sum[rt]=W[l]; return; } int m=(l+r)>>1; build(lson); build(rson); PushUp(rt); } void update(int L,int R,int c,int l,int r,int rt) { if(L<=l&&r<=R){ add[rt]=c; sum[rt]=c*(r-l+1); return; } PushDown(r-l+1,rt); int m=(l+r)>>1; if(L<=m) update(L,R,c,lson); else update(L,R,c,rson); PushUp(rt); } ll query(int L,int R,int l,int r,int rt) { if(L<=l&&r<=R){ return sum[rt]; } PushDown(r-l+1,rt); ll ans=0; int m=(l+r)>>1; if(L<=m) ans+=query(L,R,lson); if(R>m) ans+=query(L,R,rson); PushUp(rt); return ans; } void debug(int l,int r,int rt) { PushDown(r-l+1,rt); if(l==r){ cout<<l<<" "<<sum[rt]<<endl; return; } int m=(l+r)>>1; debug(lson); debug(rson); PushUp(rt); } } namespace HLD { int cnt; int top[maxn<<1],rnk[maxn<<1],dfsid[maxn<<1]; int sz[maxn<<1],fa[maxn<<1],son[maxn<<1],dep[maxn<<1]; void init() { cnt=1; cls(sz); clslow(son); } void dfs1(int u,int father,int deep) { sz[u]=1; dep[u]=deep; fa[u]=father; for(int i=head[u];~i;i=edge[i].nex){ int v=edge[i].v; if(v==fa[u]) continue; dfs1(v,u,deep+1); sz[u]+=sz[v]; if(son[u]==-1||sz[v]>sz[son[u]]){ son[u]=v; } } } void dfs2(int u,int s) { top[u]=s; dfsid[u]=cnt; rnk[cnt++]=u; if(son[u]==-1) return; dfs2(son[u],s); for(int i=head[u];~i;i=edge[i].nex){ int v=edge[i].v; if(v!=son[u]&&v!=fa[u]){ dfs2(v,v); } } } ll query(int x,int y) { ll ans=0; int fx=top[x],fy=top[y]; while(fx!=fy){ if(dep[fx]<dep[fy]) swap(x,y),swap(fx,fy); ans+=IntervalTree::query(dfsid[fx],dfsid[x],1,cnt-1,1); x=fa[fx]; fx=top[x]; } if(x==y) return ans; if(dep[x]>dep[y]) swap(x,y); ans+=IntervalTree::query(dfsid[son[x]],dfsid[y],1,cnt-1,1); return ans; } } int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif // ONLINE_JUDGE scanf("%d",&T); while(T--) { init(); int x,y,w; scanf("%d %d",&n,&q); for(int i=1;i<=n;i++){ scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w); if(vis[e[i].u]&&vis[e[i].v]){ x=e[i].u; y=e[i].u=n+1; } vis[e[i].u]=vis[e[i].v]=true; addEdge(e[i].u,e[i].v);addEdge(e[i].v,e[i].u); } HLD::init(); HLD::dfs1(1,-1,1); HLD::dfs2(1,1); for(int i=1;i<=n;i++){ if(HLD::dep[e[i].u]<HLD::dep[e[i].v]) swap(e[i].u,e[i].v); int id=HLD::dfsid[e[i].u]; W[id]=e[i].w; } IntervalTree::build(1,HLD::cnt-1,1); for(int i=1;i<=q;i++){ int op,u,v; scanf("%d %d %d",&op,&u,&v); if(op==0){ int p=HLD::dfsid[e[u].u]; IntervalTree::update(p,p,v,1,HLD::cnt-1,1); } else if(op==1){ ll ans=HLD::query(u,v); ans=min(ans,HLD::query(u,x)+HLD::query(v,y)); ans=min(ans,HLD::query(u,y)+HLD::query(v,x)); printf("%lld ",ans); } } } return 0; }
lca+树状数组

#include <queue> #include <vector> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxlog=20; const int maxn=1e5+100; ll w; int n,q,T,u,v; int tot,dfn,dfs_clock; ll bit[maxn],W[maxn]; int L[maxn],R[maxn],G[maxn],head[maxn]; int dep[maxn<<1],pos[maxn],euler_order[maxn<<1]; struct Edge { int v,nex,eid; }; Edge edge[maxn<<1]; void init() { cls(bit); clslow(pos); clslow(head); dfn=1; tot=dfs_clock=0; } void addEdge(int u,int v,int eid) { edge[tot].v=v; edge[tot].eid=eid; edge[tot].nex=head[u]; head[u]=tot++; } void dfs(int u,int deep) { L[u]=++dfs_clock; euler_order[dfn]=u; dep[dfn]=deep;pos[u]=dfn++; for(int i=head[u];~i;i=edge[i].nex){ int v=edge[i].v; int eid=edge[i].eid; if(pos[v]==-1){ G[eid]=v; dfs(v,deep+1); dep[dfn]=deep; euler_order[dfn++]=u; } } R[u]=dfs_clock; } namespace ST { int d[maxn<<1][maxlog]; void init(int n) { for(int i=1;i<=n;i++) d[i][0]=i; for(int j=1;(1<<j)<=n;j++){ for(int i=1;i+(1<<j)<=n;i++){ int l=d[i][j-1]; int r=d[i+(1<<(j-1))][j-1]; if(dep[l]<dep[r]) d[i][j]=l; else d[i][j]=r; } } } inline int query(int L,int R) { int k=0; while((1<<(k+1))<=R-L+1) k++; if(dep[d[L][k]]<dep[d[R-(1<<k)+1][k]]) return d[L][k]; return d[R-(1<<k)+1][k]; } }; inline int lca(int u,int v) { if(pos[u]>pos[v]) return euler_order[ST::query(pos[v],pos[u])]; return euler_order[ST::query(pos[u],pos[v])]; } namespace BIT { inline int lowbit(int x) { return x&-x; } inline void update(int x,ll add) { while(x<=n) { bit[x]+=add; x+=lowbit(x); } } inline ll sum(int x) { ll res=0; while(x>0) { res+=bit[x]; x-=lowbit(x); } return res; } } inline ll getdis(int u,int v) { return BIT::sum(L[u])+BIT::sum(L[v])-2*BIT::sum(L[lca(u,v)]); } int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif // ONLINE_JUDGE scanf("%d",&T); while(T--) { init(); scanf("%d %d",&n,&q); for(int i=1;i<=n;i++){ scanf("%d %d %lld",&u,&v,&w); if(i<n){ addEdge(u,v,i); addEdge(v,u,i); } W[i]=w; } dfs(1,0); ST::init(dfn-1); for(int i=1;i<n;i++){ BIT::update(L[G[i]],W[i]); BIT::update(R[G[i]]+1,-W[i]); } for(int i=1;i<=q;i++){ ll y; int op,x; scanf("%d %d %lld",&op,&x,&y); if(op==0){ if(x==n){ W[x]=y; continue; } BIT::update(L[G[x]],y-W[x]); BIT::update(R[G[x]]+1,-y+W[x]); W[x]=y; } else { ll ans=getdis(x,y); ans=min(ans,getdis(x,u)+getdis(y,u)); ans=min(ans,getdis(x,v)+getdis(y,v)); ans=min(ans,getdis(x,u)+getdis(y,v)+w); ans=min(ans,getdis(x,v)+getdis(y,u)+w); printf("%lld ",ans); } } } return 0; }
Sequence
题意:
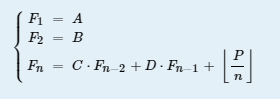 ,给出A,B,C,D,P,n,求Fn。
,给出A,B,C,D,P,n,求Fn。
分析:
对于P/n为定值(1,2……n)的区间用矩阵快速幂加速即可。
代码:

#include <set> #include <queue> #include <vector> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int mod=1e9+7; const int maxn=1e5+100; const int MatrixSize=3; int a,b,c,d,p,n,T; struct Matrix{ ll mat[10][10]; Matrix operator *(Matrix a) { Matrix res; for(int i=0;i<MatrixSize;i++){ for(int j=0;j<MatrixSize;j++){ res.mat[i][j]=0; for(int k=0;k<MatrixSize;k++){ res.mat[i][j]=(res.mat[i][j]+mat[i][k]*a.mat[k][j])%mod; } } } return res; } void show() { for(int i=0;i<MatrixSize;i++){ for(int j=0;j<MatrixSize;j++){ printf("%d ",mat[i][j]); } printf(" "); } printf("################# "); } }; Matrix ans,temp,res; void init(ll a1,ll a2,ll x) { cls(temp.mat); temp.mat[0][0]=d%mod; temp.mat[1][0]=c%mod; temp.mat[0][1]=1; temp.mat[2][2]=1; temp.mat[2][0]=x; cls(ans.mat); ans.mat[0][0]=a1%mod; ans.mat[0][1]=a2%mod; ans.mat[0][2]=1; } Matrix poww(Matrix ans,int k) { while(k) { if(k&1) ans=ans*temp; temp=temp*temp; k>>=1; } return ans; } int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif scanf("%d",&T); while(T--) { scanf("%d %d %d %d %d %d",&a,&b,&c,&d,&p,&n); if(n<=2){ if(n==1) printf("%lld ",a%mod); else if(n==2) printf("%lld ",b%mod); continue; } res.mat[0][0]=b%mod; res.mat[0][1]=a%mod; for(int i=3;i<=n;){ ll j=(p/i==0?n:min(n,p/(p/i))); init(res.mat[0][0],res.mat[0][1],p/i); res=poww(ans,j-i+1); i=j+1; } printf("%lld ",res.mat[0][0]); } return 0; }
Swordsman
题意:
人和怪物有k个属性,如果人的每个属性都大于等于怪物的属性,那么人可以杀掉这个怪物,并且人的每个属性对应加上怪物贡献的属性值,输出人最多能杀几只怪物和人的属性值。
分析:
考虑把所有怪物加入一个优先队列中(按照第一个属性排序),将怪物属性小于等于人的第一个属性的怪物加入第二个优先队列中(按照第二个属性排序)……直到最后找不到一个怪物的所有属性值都小于等于人的属性值时结束。
代码:

#include <set> #include <queue> #include <vector> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) #define FI(n) FastIO::read(n) namespace FastIO { const int SIZE = 1 << 16; char buf[SIZE], obuf[SIZE], str[60]; int bi = SIZE, bn = SIZE, opt; int read(char *s) { while (bn) { for (; bi < bn && buf[bi] <= ' '; bi++); if (bi < bn) break; bn = fread(buf, 1, SIZE, stdin); bi = 0; } int sn = 0; while (bn) { for (; bi < bn && buf[bi] > ' '; bi++) s[sn++] = buf[bi]; if (bi < bn) break; bn = fread(buf, 1, SIZE, stdin); bi = 0; } s[sn] = 0; return sn; } bool read(int& x) { int n = read(str), bf; if (!n) return 0; int i = 0; if (str[i] == '-') bf = -1, i++; else bf = 1; for (x = 0; i < n; i++) x = x * 10 + str[i] - '0'; if (bf < 0) x = -x; return 1; } }; const int maxk=7; const int maxn=1e5+100; int n,k,T; int v[maxk]; struct Monster { int b[maxk],v[maxk]; }; Monster m[maxn]; priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >que[maxk]; int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); #endif FI(T); while(T--) { FI(n);FI(k); for(int i=1;i<maxk;i++){ while(!que[i].empty()) que[i].pop(); } for(int i=1;i<=k;i++) FI(v[i]); for(int i=1;i<=n;i++){ for(int j=1;j<=k;j++) FI(m[i].v[j]); for(int j=1;j<=k;j++) FI(m[i].b[j]); que[1].push(make_pair(m[i].v[1],i)); } int cnt=0; while(true) { for(int i=2;i<=k+1;i++){ while(!que[i-1].empty()) { int id=que[i-1].top().second; int value=que[i-1].top().first; if(value<=v[i-1]){ que[i].push(make_pair(m[id].v[i],id)); que[i-1].pop(); } else break; } } if(que[k+1].empty()) break; while(!que[k+1].empty()) { cnt++; int id=que[k+1].top().second; for(int i=1;i<=k;i++){ v[i]+=m[id].b[i]; } que[k+1].pop(); } } printf("%d ",cnt); for(int i=1;i<=k;i++){ if(i>1) printf(" "); printf("%d",v[i]); if(i==k) printf(" "); } } return 0; }
