一、用赋值的方法可以扩展一个已知的数组:
arr= 1:1:4;
arr(8)=6;
此时,arr = 1 2 3 4 0 0 0 6
arrNew=arr;
此时arrNew = 1 2 3 4 0 0 0 6。
由上面可以看出,每一次扩展数组,都要经过以下
步骤:第一步,创建一个新数组。第二步,把旧数组的元素复制到新数组当中。第三步,把
扩展的元素写入新数组。第四步,删除旧数组。对于大数组来说这些步骤是相当耗时的。
二、用向量法
好的编程习惯
在循环执行开始之前 ,总是要预先分配一个数组,这样能大大增加循环运行的速度。
所以
用向量语句它的执行速度非常快。
向量算法的缺点是需要很大的内存, 因为一些间接的数组需要创建。 这就是向量算法的一个小缺点,但它的执行速度比 for 循环算法快得多。
在 MATLAB 中, 用向量算法代替循环的算法的过程称之为向量化(vectorization)。 向量化能够改进许多的 MATLAB 程序。
比较向量算法和循环
为了比较循环和向量算法执行所用的时间,用两种方法编程并测试三个运算所花的时
间。
1.用 for 循环计算 1 到 10000 的之间每一个整数的平方,而事先不初始化平方数组。
2.用 for 循环计算 1 到 10000 的之间每一个整数的平方,而事先初始化平方数组。
3.用向量算法计算 1 到 10000 的之间每一个整数的平方。
答案:
这个程序必须用上面提供的三种方式计算出 1 到 10000 之间的每一个整数的平方, 并测
试每一个种算法的时间。测试时间要用到 MATLAB 函数 tic 和 toc。tic 函数复位内建计时器,
而 toc 函数则从最后一次调用 tic 以秒开始计时。
因为在许多的计算机中它的时间钟是相当粗略的, 所以有必要多运行几次以获得相应的
平均数。
% 脚本文件 times.m % % 目标: % 该程序用三种方式测量整数从1到10000的平方所用的时间 % % 1. 用for循环,没有初始化平方数组 % 2. 用for循环,初始化平方数组 % 3. 用向量法计算 % %版本记录 % 日期 编者 变化描述 % ==== ========== ===================== % 2015-10-5 18:12 泡泡 源代码 % % 定义变量 % ii, jj 循环索引 % average1 用方式1计算所用平均时间 % average2 用方式2计算所用平均时间 % average3 用方式3计算所用平均时间 % maxcount 循环次数 % square 平方数组 % %----------------------------------------------------------------- % for循环:没有初始化平方数组 % 循环1次 % 因为很慢 maxcount = 1; % 1次重复 tic; % 计时开始 for jj = 1:maxcount clear square % 把以前是这个变量名的清除 for ii = 1:10000 square(ii) = ii^2; % 平方计算 end end average1 = (toc)/maxcount; % 所用时间平均值 %----------------------------------------------------------------- % for循环:初始化平方数组 % 循环10次 % 对比作用 maxcount = 10; % 10次重复 tic; % 计时开始 for jj = 1:maxcount clear square % Clear变量 square = zeros(1,10000); % 初始化平方数组,全部值为0 for ii = 1:10000 square(ii) = ii^2; % 平方计算 end end average2 = (toc)/maxcount; % 所用时间平均值 %----------------------------------------------------------------- % 用向量法计算 % 循环100次 % 因为非常快 maxcount = 100; % 100次重复 tic; % 计时开始 for jj = 1:maxcount clear square % Clear变量 ii = 1:10000; % Set up vector square = ii.^2; % 平方计算 end average3 = (toc)/maxcount; % 所用时间平均值 % 结果对比显示 fprintf('for 循环 / 没有初始化数组 = %8.4f ', average1); fprintf('for 循环/ 初始化数组 = %8.4f ', average2); fprintf('用向量法 = %8.4f ', average3);
结果:
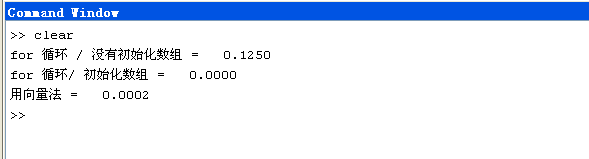
可以看到,用初始化了数组合向量法几乎不耗费时间
好的编程习惯
那种既可以用向量可以解决的问题,也可以用循环解决的问题,最好用向量解决,这
是因为向量执行的速度快。