HashMap中tableSizeFor

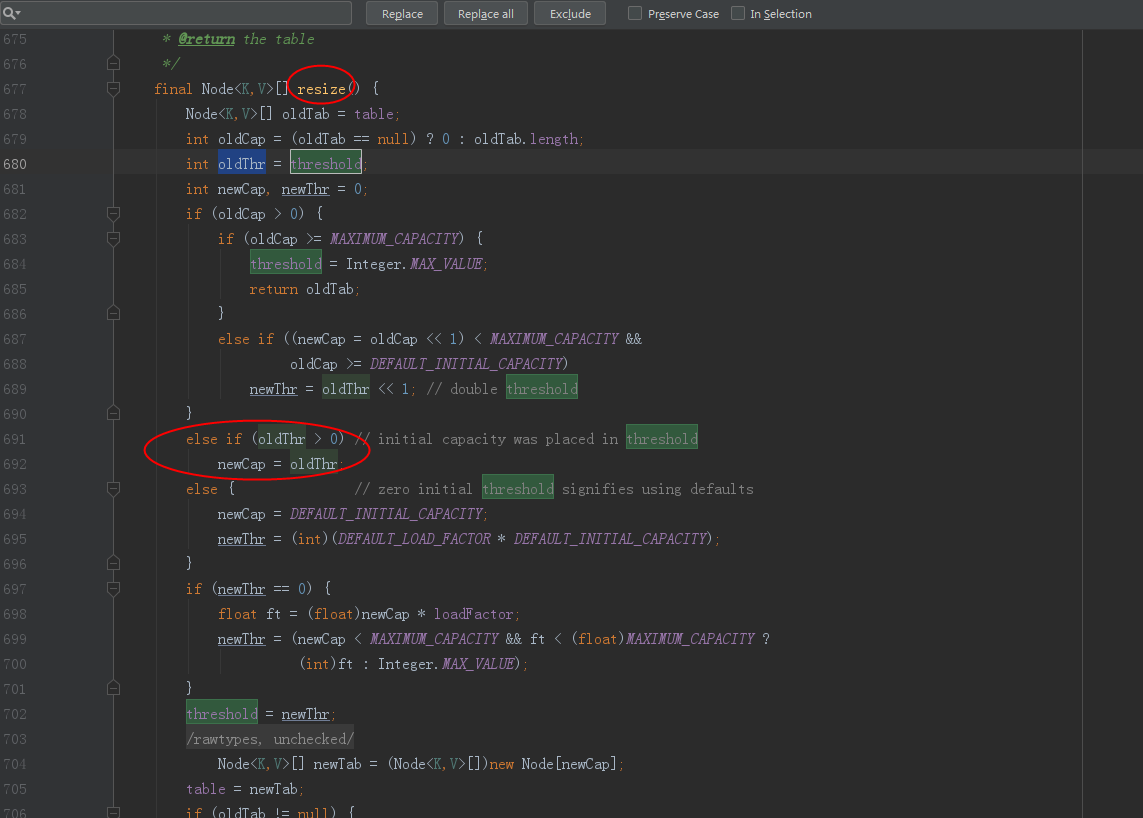
    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

这个方法被调用的地方：

    public HashMap(int initialCapacity, float loadFactor) {
        /**省略此处代码**/
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }

由此可以看到，当在实例化HashMap实例时，如果给定了initialCapacity，由于HashMap的capacity都是2的幂，因此这个方法用于找到大于等于initialCapacity的最小的2的幂（initialCapacity如果就是2的幂，则返回的还是这个数）。 
下面分析这个算法： 
首先，为什么要对cap做减1操作。int n = cap - 1; 
这是为了防止，cap已经是2的幂。如果cap已经是2的幂， 又没有执行这个减1操作，则执行完后面的几条无符号右移操作之后，返回的capacity将是这个cap的2倍。如果不懂，要看完后面的几个无符号右移之后再回来看看。 
下面看看这几个无符号右移操作： 
如果n这时为0了（经过了cap-1之后），则经过后面的几次无符号右移依然是0，最后返回的capacity是1（最后有个n+1的操作）。 
这里只讨论n不等于0的情况。 
第一次右移

n |= n >>> 1;

由于n不等于0，则n的二进制表示中总会有一bit为1，这时考虑最高位的1。通过无符号右移1位，则将最高位的1右移了1位，再做或操作，使得n的二进制表示中与最高位的1紧邻的右边一位也为1，如000011xxxxxx。 
第二次右移

n |= n >>> 2;

注意，这个n已经经过了n |= n >>> 1; 操作。假设此时n为000011xxxxxx ，则n无符号右移两位，会将最高位两个连续的1右移两位，然后再与原来的n做或操作，这样n的二进制表示的高位中会有4个连续的1。如00001111xxxxxx 。 
第三次右移

n |= n >>> 4;

这次把已经有的高位中的连续的4个1，右移4位，再做或操作，这样n的二进制表示的高位中会有8个连续的1。如00001111 1111xxxxxx 。 
以此类推 
注意，容量最大也就是32bit的正数，因此最后n |= n >>> 16; ，最多也就32个1，但是这时已经大于了MAXIMUM_CAPACITY ，所以取值到MAXIMUM_CAPACITY 。 
举一个例子说明下吧。 

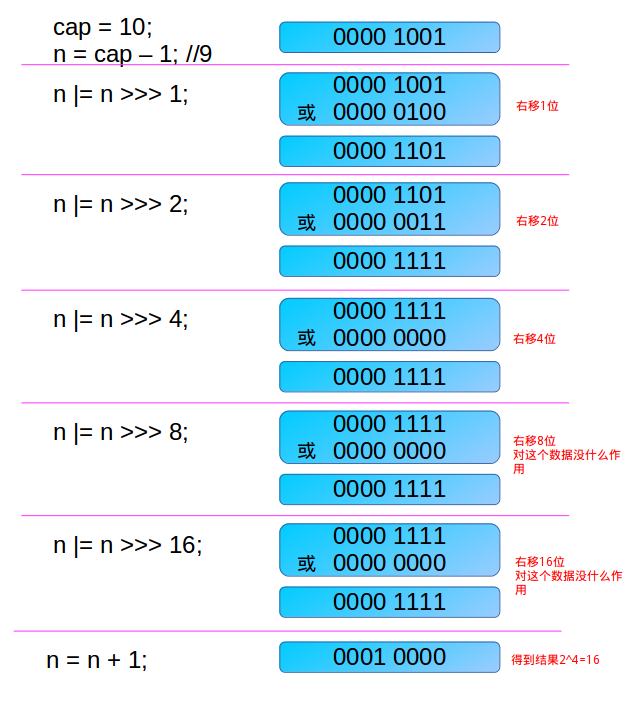
这个算法着实牛逼啊！

注意，得到的这个capacity却被赋值给了threshold。

this.threshold = tableSizeFor(initialCapacity);

开始以为这个是个Bug，感觉应该这么写：

this.threshold = tableSizeFor(initialCapacity) * this.loadFactor;

这样才符合threshold的意思（当HashMap的size到达threshold这个阈值时会扩容）。 
但是，请注意，在构造方法中，并没有对table这个成员变量进行初始化，table的初始化被推迟到了put方法中，在put方法中会对threshold重新计算

后面再进行put操作中会使用这个threshold 进行操作