kruskal算法和prim算法
都说 kruskal是加边法,prim是加点法
这篇解释也不错:这篇
1、kruskal算法
因为是加边法,所以这个方法比较合适稀疏图。要码这个需要先懂并查集。因为我不会画好看的图,所以看不懂的话推荐下面博客的说明。这里是下面。
步骤:
1、把每个点都看成一棵树,那么你就会得到一片森林。。。
2、把每棵树之间的距离从小到大排序,即把边排序
3、从小到大取边,把不在同一棵树的点连通到同一棵树上。。。最后你会得到一棵树,就是最小生成树
我去盗图。。。这里的图
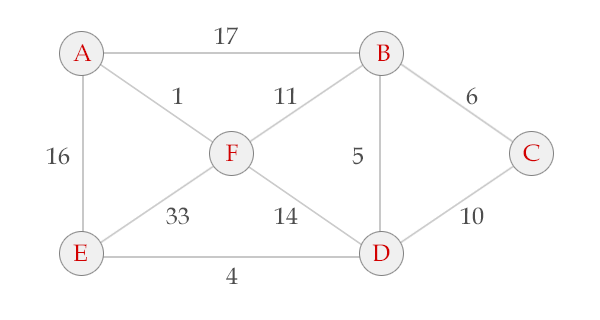
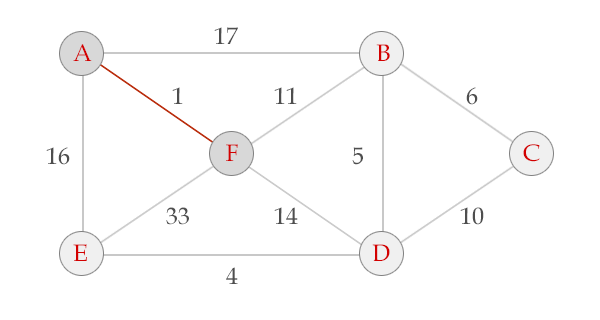
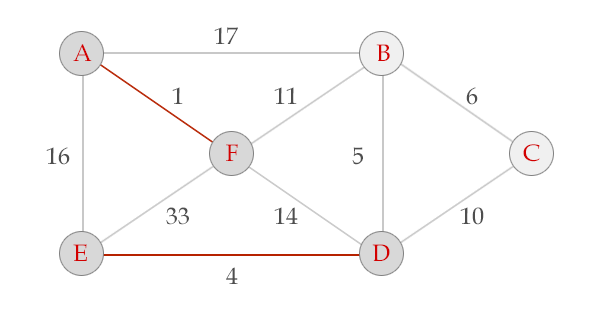
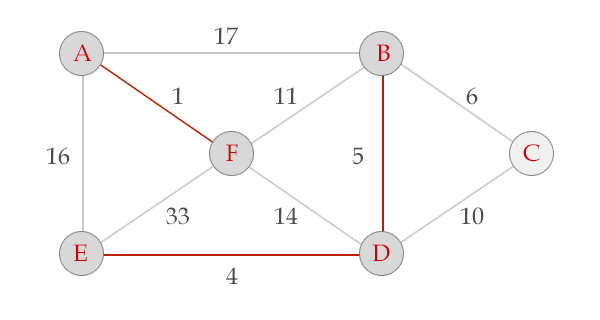
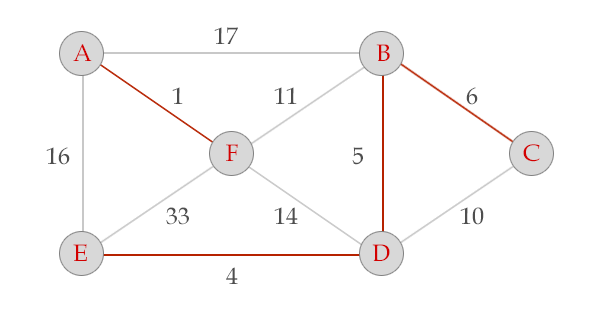
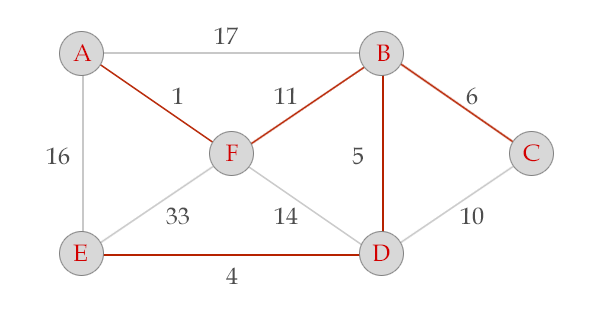
给个模板题吧。。HDU1233
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 5005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) struct Edge { int u, v, w; bool operator < (const Edge &a) const { return w < a.w; } }edge[MAXN]; int n, ans, fa[105]; //找父节点并压缩路径,这是并查集的知识 int Get_f(int x) { if(fa[x] == x) return x; return fa[x] = Get_f(fa[x]); } void Kruskal() { //初始化 for(int i = 1;i <= n;++i) fa[i] = i; sort(edge, edge + (n - 1) * n / 2); ans = 0; int x, y, cnt = 1; for(int i = 0;i < n * (n - 1) / 2;++i) { x = Get_f(edge[i].u), y = Get_f(edge[i].v); //加边 if(x != y) { ans += edge[i].w; fa[x] = y; cnt++; } //加入所有点了 if(cnt >= n) break; } printf("%d ", ans); } int main() { while(scanf("%d", &n) != EOF && n) { for(int i = 0;i < n * (n - 1) / 2;++i) scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].w); Kruskal(); } return 0; }
2、Prim算法
这算法写起来跟最短路的 Dijkstra算法很像。来复习一下 Dijkstra算法,先找出距离源点最短的点(这里是找出离一个点最近的路),然后把这个点与。源点连接(这里是连接这两个点),之后再更新最短路(更新到各个点的最短的边,这里代码有点不同)。。。就没有哈哈哈哈。。。直接上上面那道模板题代码吧。。。。。
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 1005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) int mp[MAXN][MAXN], dis[MAXN], n, ans; bool vis[MAXN]; void Prim(int s) { Mem0(vis); int i, j; for(i = 1;i <= n;++i) dis[i] = mp[s][i]; dis[s] = 0; int v, w; vis[s] = true; for(i = 1;i < n;++i) { w = INF; for(j = 1;j <= n;++j) { if(!vis[j] && dis[j] < w) { w = dis[j]; v = j; } } vis[v] = true; ans += w; for(j = 1;j <= n;++j) if(!vis[j] && dis[j] > mp[v][j])//这里不同 dis[j] = mp[v][j]; } printf("%d ", ans); } int main() { int a, b, c; while(scanf("%d", &n) != EOF && n) { MemM(mp); ans = 0; for(int i = 0;i < n * (n - 1) / 2;++i) { scanf("%d%d%d", &a, &b, &c); mp[a][b] = mp[b][a] = c; } Prim(1); } return 0; }
3、 STL与kruskal(理论上 Prim算法应该能用优先队列简化找最短路径的操作,就。。不码这个了)
用map存边,简化排序操作。。。先是模板题练练手,可是跑出来时间慢了十几毫秒
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 1005; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) int ans, n, fa[MAXN]; int Get_F(int x) { if(fa[x] == x) return x; return fa[x] = Get_F(fa[x]); } int main() { while(scanf("%d", &n) != EOF && n) { ans = 0; multimap<int, pair<int, int> > mp; for(int i = 1;i <= n;++i) fa[i] = i; int a, b, c; for(int i = 0;i < n * (n - 1) / 2;++i) { scanf("%d%d%d", &a, &b, &c); mp.insert(make_pair(c, make_pair(a, b))); } multimap<int, pair<int, int> > :: iterator it; int x, y; for(it = mp.begin();it != mp.end();++it) { x = Get_F((*it).second.first), y = Get_F((*it).second.second); if(x != y) { fa[x] = y; ans += (*it).first; } } printf("%d ", ans); } return 0; }
再给多一道题 UVALive - 6437 ,先用Prim写一下,感觉Prim比较容易理解,然后再用 kruskal写个简单版的。
Prim思路:。。。。下面注释吧。
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 205; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) //点数 n,边数 m ,发电站数量 num, 图 mp, 发电站 power int ans, n, m, num, vis[MAXN], dis[MAXN], mp[MAXN][MAXN]; int power[MAXN]; int Prim() { int i, j, k; // 各个城镇到各个发电站的最短距离 MemM(dis); for(i = 1;i <= n;++i) for(j = 0;j < num;++j) dis[i] = min(dis[i], mp[i][power[j]]); int w, v; // 还要对 n - num 个点找最短路 for(i = 0;i < n - num;++i) { w = INF; for(j = 1;j <= n;++j) if(!vis[j] && dis[j] < w) { w = dis[j]; v = j; } vis[v] = true; ans += w; // 这里可以理解为城镇新建了发电站,就看其他城镇到这个新发电站的距离 for(j = 1;j <= n;++j) if(!vis[j] && dis[j] > mp[v][j]) dis[j] = mp[v][j]; } return ans; } int main() { int T; scanf("%d", &T); for(int cas = 1;cas <= T;++cas) { MemM(mp); Mem0(vis); ans = 0; scanf("%d%d%d", &n, &m, &num); for(int i = 1;i <= n;++i) mp[i][i] = 0; int a, b, c; for(int i = 0;i < num;++i) { scanf("%d", &power[i]); vis[power[i]] = true;//这里先处理发电站比较方便 } for(int i = 0;i < m;++i) { scanf("%d%d%d", &a, &b, &c); mp[a][b] = mp[b][a] = c; } printf("Case #%d: %d ", cas, Prim()); } return 0; }
Kruskal。。。这道题把所有发电站都先放到一个集合里,那么最后出来的最小生成树就是答案了。。。。具体点就是把所有发电站的祖先都设为同一个,这样不管连接哪一个发电站都有共同祖先。
慢了30ms左右
#include <iostream> #include <cstdio> #include <string> #include <cstring> #include <cmath> #include <sstream> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <iomanip> #include <stack> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int MAXN = 205; const int MOD = 1e9 + 7; #define MemI(x) memset(x, -1, sizeof(x)) #define Mem0(x) memset(x, 0, sizeof(x)) #define MemM(x) memset(x, 0x3f, sizeof(x)) int ans, n, m, k, fa[MAXN]; int Get_F(int x) { if(fa[x] == x) return x; return fa[x] = Get_F(fa[x]); } int main() { int T; scanf("%d", &T); for(int cas = 1;cas <= T;++cas) { multimap<int, pair<int, int> > mp; multimap<int, pair<int, int> > :: iterator it; ans = 0; scanf("%d%d%d", &n, &m, &k); for(int i = 1;i <= n;++i) fa[i] = i; int a, b, c; //处理发电站 scanf("%d", &a); for(int i = 1;i < k;++i) { scanf("%d", &b); fa[b] = a; } for(int i = 0;i < m;++i) { scanf("%d%d%d", &a, &b, &c); mp.insert(make_pair(c, make_pair(a, b))); } ans = 0; int x, y; for(it = mp.begin();it != mp.end();++it) { x = Get_F((*it).second.first), y = Get_F((*it).second.second); if(x != y) { ans += (*it).first; fa[x] = y; } } printf("Case #%d: %d ", cas, ans); } return 0; }