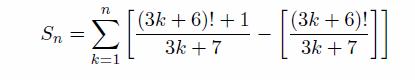威尔逊定理--HDU2973

参考博客
HDU-2973

题目

Problem Description

The math department has been having problems lately. Due to immense amount of unsolicited automated programs which were crawling across their pages, they decided to put Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on their webpages. In short, to get access to their scientific papers, one have to prove yourself eligible and worthy, i.e. solve a mathematic riddle.

However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).

The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute

where [x] denotes the largest integer not greater than x.

Input

The first line contains the number of queries t (t <= 10^6). Each query consist of one natural number n (1 <= n <= 10^6).

Output

For each n given in the input output the value of Sn.

Sample Input

13
1
2
3
4
5
6
7
8
9
10
100
1000
10000

Sample Output

0
1
1
2
2
2
2
3
3
4
28
207
1609

思路

威尔逊定理及其逆定理、前缀和

威尔逊定理：当且仅当p为素数时：

[(p-1)!equiv -1(mod p) ]

否则

[(p-1)!equiv 0(mod p) ]

设

[a_n=[frac {(3k+6)!+1}{3k+7}-[frac {(3k+6)!}{3k+7}]] ]

所以当（3k+7)为素数时，a_n为1，否则为0

[[frac {(3k+6)!+1}{3k+7}-[frac {(3k+6)!}{3k+7}]]=[frac {kp+p-1+1}{p}-[frac {kp+p-1}{p}]]=[k+1-k]=1 ]

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <string>
#include <algorithm>

using namespace std;

typedef long long LL;
const int maxn=1e6+5;
const double pi = acos(-1);
const int mod=1e9+7;
const int N = 1000005;

int vis[N * 4], p[N * 4];
int ans[N];
void Init()\埃式筛
{
    for(int i = 2;(i - 7) / 3 < N;++i)
    {
        if(!vis[i])
        {
            if((i - 7) % 3 == 0)
                p[(i - 7) / 3] = 1;
            for(int j = i + i;j <= N * 4;j += i)
                vis[j] = true;
        }
    }
    for(int i = 1;i < N;++i)
        ans[i] = ans[i - 1] + p[i];
}

int main()
{
    Init();
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        cin >> n;
        cout << ans[n] << endl;
    }
    return 0;
}

[素数定理]（https://en.wikipedia.org/wiki/Dirichlet's_theorem_on_arithmetic_progressions）
当a、b为素数时，则形如 a+nb 的素数有无穷多个