题目链接:https://www.luogu.org/problem/P3389
题意:给你方程组,如果存在多组解,输入 No solution,如果有唯一解,输出唯一解。

比如上面这个方程组,怎么用计算机解?
高斯消元算法描述:看大佬文章吧,比我写的好,总的思路就是矩阵的行列式变化。最后把行列式变成上三角形状,盗用女装大佬的一个图
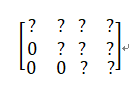
图上最后一列是方程右边的值,前面的列是变换后的系数,可以发现,在最后一行就只有一个系数,求出最后一行的变量解后,倒数第二行也就只要求一个变量。
大佬博客地址:
https://45475.blog.luogu.org/linear-equation-group
import java.io.BufferedReader; import java.io.File; import java.io.FileInputStream; import java.io.IOException; import java.io.InputStream; import java.io.InputStreamReader; import java.util.Scanner; import java.util.StringTokenizer; public class Main { static Scanner scanner; static int N = 110; // static int N = 5; static double[][] a = new double[N][N]; static double[] result = new double[N]; static int n; public static void init() { for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { a[i][j] = 0; } result[i] = 0; } } public static void main(String[] args) throws IOException { InputStream in = System.in; //InputStream in = new FileInputStream(new File("D://1.text")); Reader.init(in); n = Reader.nextInt(); // Reader.next(); for (int i = 0; i < n; i++) { for (int j = 0; j <= n; j++) { a[i][j] = Reader.nextInt(); } } // 高斯消元算法 for (int c = 0; c < n - 1; c++) { int maxR = c; // 寻找最大值的行 for (int i = maxR + 1; i < n; i++) { if (Math.abs(a[i][c]) > Math.abs(a[maxR][c])) { maxR = i; } } if (maxR != c) { swapRow(maxR, c, n + 1); maxR = c; } dump(); // 检查a[maxR][c] 是否等于0 if (a[maxR][c] == 0) { break; } for (int r = c + 1; r < n; r++) { // 判断a[r][c]是否是0 if (a[r][c] == 0) { // 当前的列已经等于0,不用再消元 continue; } // 对当前行的每一列开始减数 double val = a[maxR][c] / a[r][c]; for (int c2 = c; c2 <= n; c2++) { a[r][c2] = a[r][c2] * val - a[maxR][c2]; } } dump(); } // 判断是否无解 int solution = 1; for (int i = 0; i < n; i++) if ((a[i][i] == 0 && a[i][n] != 0) || (a[i][i] == 0 && a[i][n] ==0)) { solution = 0; break; } if (solution == 0) { System.out.println("No Solution"); } else { // 求解 int k = 0; for (int i = n - 1; i >= 0; i--) { double total = 0; for (int j = 0; j < k; j++) { total += result[n - j - 1] * a[i][n - j - 1]; } if (a[i][n - 1 - k] == 0) { result[i] = 1; } else { result[i] = (a[i][n] - total) / a[i][n - 1 - k]; } k++; } for (int i = 0; i < n; i++) { System.out.printf("%.2f ", result[i]); } } } static void dump() { // for (int i = 0; i < n; i++) // { // for (int j = 0; j <= n; j++) // { // System.out.print(" " + a[i][j]); // } // System.out.println(); // } // System.out.println(); // System.out.println(); } static void swapRow(int i, int j, int n) { for (int c = 0; c < n; c++) { double t = a[j][c]; a[j][c] = a[i][c]; a[i][c] = t; } } static class Reader { static BufferedReader reader; static StringTokenizer tokenizer; /** call this method to initialize reader for InputStream */ static void init(InputStream input) { reader = new BufferedReader(new InputStreamReader(input)); tokenizer = new StringTokenizer(""); } /** get next word */ static String next() throws IOException { while (!tokenizer.hasMoreTokens()) { String s = reader.readLine(); if (s == null) return s; tokenizer = new StringTokenizer(s); } return tokenizer.nextToken(); } static int nextInt() throws IOException { return Integer.parseInt(next()); } static double nextDouble() throws IOException { return Double.parseDouble(next()); } } }