https://blog.csdn.net/u013709270/article/details/49642397
https://github.com/xuewenyuan/Gabor_Visualization
https://blog.csdn.net/u013709270/article/details/49642397
第三种
使用的第三种gabor模型:

代码opencv实现
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <math.h>
cv::Mat mkKernel(int ks, double sig, double th, double lm, double ps)
{
int hks = (ks-1)/2;
double theta = th*CV_PI/180;
double psi = ps*CV_PI/180;
double del = 2.0/(ks-1);
double lmbd = lm;
double sigma = sig/ks;
double x_theta;
double y_theta;
cv::Mat kernel(ks,ks, CV_32F);
for (int y=-hks; y<=hks; y++)
{
for (int x=-hks; x<=hks; x++)
{
x_theta = x*del*cos(theta)+y*del*sin(theta);
y_theta = -x*del*sin(theta)+y*del*cos(theta);
kernel.at<float>(hks+y,hks+x) = (float)exp(-0.5*(pow(x_theta,2)+pow(y_theta,2))/pow(sigma,2))* cos(2*CV_PI*x_theta/lmbd + psi);
}
}
return kernel;
}
int kernel_size=21;
int pos_sigma= 5;
int pos_lm = 50;
int pos_th = 0;
int pos_psi = 90;
cv::Mat src_f;
cv::Mat dest;
void Process(int , void *)
{
double sig = pos_sigma;
double lm = 0.5+pos_lm/100.0;
double th = pos_th;
double ps = pos_psi;
cv::Mat kernel = mkKernel(kernel_size, sig, th, lm, ps);
cv::imshow("kernel window", kernel);
cv::filter2D(src_f, dest, CV_32F, kernel);
cv::imshow("Process window", dest);
cv::Mat Lkernel(kernel_size*20, kernel_size*20, CV_32F);
cv::resize(kernel, Lkernel, Lkernel.size());
Lkernel /= 2.;
Lkernel += 0.5;
cv::imshow("Kernel", Lkernel);
cv::Mat mag;
cv::pow(dest, 2.0, mag);
cv::imshow("Mag", mag);
}
int main(int argc, char** argv)
{
cv::Mat image = cv::imread("1.jpg",1);
cv::imshow("Src", image);
cv::Mat src;
cv::cvtColor(image, src, CV_BGR2GRAY);
src.convertTo(src_f, CV_32F, 1.0/255, 0);
if (!kernel_size%2)
{
kernel_size+=1;
}
cv::namedWindow("Process window", 1);
cv::createTrackbar("Sigma", "Process window", &pos_sigma, kernel_size, Process);
cv::createTrackbar("Lambda", "Process window", &pos_lm, 100, Process);
cv::createTrackbar("Theta", "Process window", &pos_th, 180, Process);
cv::createTrackbar("Psi", "Process window", &pos_psi, 360, Process);
Process(0,0);
cv::waitKey(0);
return 0;
}
第四种 :最完整的变化:代码在下面
二、Gabor函数
Gabor变换属于加窗傅立叶变换,Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。另外Gabor函数与人眼的生物作用相仿,所以经常用作纹理识别上,并取得了较好的效果。二维Gabor函数可以表示为:

其中:

v的取值决定了Gabor滤波的波长,u的取值表示Gabor核函数的方向,K表示总的方向数。参数![]() 决定了高斯窗口的大小,这里取
决定了高斯窗口的大小,这里取![]() 。程序中取4个频率(v=0, 1, ..., 3),8个方向(即K=8,u=0, 1, ... ,7),共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示:
。程序中取4个频率(v=0, 1, ..., 3),8个方向(即K=8,u=0, 1, ... ,7),共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示:


图片来源:GaborFilter.html

图片来源:http://www.bmva.ac.uk/bmvc/1997/papers/033/node2.html
三、代码实现
Gabor函数是复值函数,因此在运算过程中要分别计算其实部和虚部。代码如下:
private void CalculateKernel(int Orientation, int Frequency)
{
double real, img;
for(int x = -(GaborWidth-1)/2; x<(GaborWidth-1)/2+1; x++)
for(int y = -(GaborHeight-1)/2; y<(GaborHeight-1)/2+1; y++)
{
real = KernelRealPart(x, y, Orientation, Frequency);
img = KernelImgPart(x, y, Orientation, Frequency);
KernelFFT2[(x+(GaborWidth-1)/2) + 256 * (y+(GaborHeight-1)/2)].Re = real;
KernelFFT2[(x+(GaborWidth-1)/2) + 256 * (y+(GaborHeight-1)/2)].Im = img;
}
}
private double KernelRealPart(int x, int y, int Orientation, int Frequency)
{
double U, V;
double Sigma, Kv, Qu;
double tmp1, tmp2;
U = Orientation;
V = Frequency;
Sigma = 2 * Math.PI * Math.PI;
Kv = Math.PI * Math.Exp((-(V+2)/2)*Math.Log(2, Math.E));
Qu = U * Math.PI / 8;
tmp1 = Math.Exp(-(Kv * Kv * ( x*x + y*y)/(2 * Sigma)));
tmp2 = Math.Cos(Kv * Math.Cos(Qu) * x + Kv * Math.Sin(Qu) * y) - Math.Exp(-(Sigma/2));
return tmp1 * tmp2 * Kv * Kv / Sigma;
}
private double KernelImgPart(int x, int y, int Orientation, int Frequency)
{
double U, V;
double Sigma, Kv, Qu;
double tmp1, tmp2;
U = Orientation;
V = Frequency;
Sigma = 2 * Math.PI * Math.PI;
Kv = Math.PI * Math.Exp((-(V+2)/2)*Math.Log(2, Math.E));
Qu = U * Math.PI / 8;
tmp1 = Math.Exp(-(Kv * Kv * ( x*x + y*y)/(2 * Sigma)));
tmp2 = Math.Sin(Kv * Math.Cos(Qu) * x + Kv * Math.Sin(Qu) * y) - Math.Exp(-(Sigma/2));
return tmp1 * tmp2 * Kv * Kv / Sigma;
}
有了Gabor核函数后就可以采用前文中提到的“离散二维叠加和卷积”或“快速傅立叶变换卷积”的方法求解Gabor变换,并对变换结果求均值和方差作为提取的特征。32个Gabor核函数对应32次变换可以提取64个特征(包括均值和方差)。由于整个变换过程代码比较复杂,这里仅提供测试代码供下载。该代码仅计算了一个101×101尺寸的Gabor函数变换,得到均值和方差。代码采用两种卷积计算方式,从结果中可以看出,快速傅立叶变换卷积的效率是离散二维叠加和卷积的近50倍。
代码下载请点 >>>> 这里 。注意,代码中没有包含Exocortex.DSP,请测试者到相应网站上下载并包含在自己的项目中。
解压缩后,里面有一"GaborTest.png"文件,程序中默认路径是“D:”,请将此图片放置到此路径下。(程序代码在Visual Studio .net 2003下调试通过)。
1.Introduction
下面开始介绍Gabor 滤波器以及相关的知识,首先上wiki上关于Gabor filter的介绍:In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for edge detection. Frequency and orientation representations of Gabor filters are similar to those of the human visual system, and they have been found to be particularly appropriate for texture representation and discrimination. In the spatial domain, a 2D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plane wave.说白了就是说这个滤波器与视觉通路信息处理结构很相似,从信号处理的角度上是一个正弦波平面波调制的高斯函数,公式和图如下:
-------------------------------------------- 1
Real part:
-------------------------------------------------------- 2
Imaginary part:
--------------------------------------------------------- 3
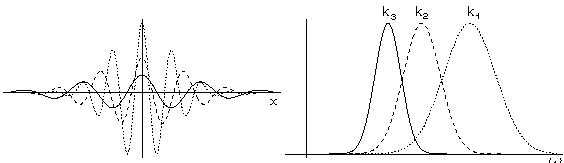
解释一下参数:lamda 是波长,不同波长的效果如下:
, heta 是角度,如果想得到不同方向上的滤波器的话,就需要做旋转,我们知道这个可以通过乘上一个旋转矩阵得到:
-------------------------------------------------------------------- 4
下面展示的就是不同角度的Gabor filter:
上面两个是最关键的参数,我们常说Gabor filter可以得到多尺度多方向的响应,其实就是这两个参数在起作用。其他参数phi指的是phase offset, gamma 指的是aspect ratio,也就是x方向和y方向的比例,具体各个参数的效果参考:http://matlabserver.cs.rug.nl/edgedetectionweb/web/edgedetection_params.html
而二维Gabor在三维下显示的样子就是:
如果没有正弦调制,二维高斯就是平滑的一个凸起,现在因为有了正弦波调制,就有了这种沟壑。而不要小看了这个沟壑,从图像处理的角度来讲:傅立叶变换在很大程度上只是一个体现大局观的概念,而无法反映图像局部的特点,,因此我们无法通过傅立叶变换来对图像进行细节上更准确的操作。幸运的是,人们之后的研究中,发现了Gabor于1946年发表的论文《the Theory of Communication》,于是在识别的方法上,尤其在纹理识别上达到了一个新的高度。当然小波变换的应用也是差不多这个时间段开始的,由此我们也可以理解数学在图像领域的价值[1].
===========================================理论==========================================
下面我再从公式开始重新展示一下Gabor filter,目的就是为了解释为什么会出现我一开始说的多种版本的Gabor filter。其实,我也正是因为搞不懂这个,才重新研究Gabor filter。
Part 1;高斯正弦平面波
我们已经说过Gabor filter是用正弦平面波调制高斯,先说正弦平面波,也就是是二维的正弦波,公式表达为:------- 5,
我们可视化之后样子如下:
当然,最标准的complex sinusoid 函数形式是:------------------------------------- 6,
两者的区别在于后者得到的曲面不是与x轴平行的而是旋转了45度,考虑到可以对 heta采用旋转得到一样的效果,所以两个形式的函数都是可以的,我们采用第二种形式(公式6)。
Part 2 高斯权重分布或者Gaussian envelope
二维高斯分布的标准形式为:
---------------------------------------------------------------- 7
如果令,那么上式就可以写成:
----------------------------------------------------------- 8
其中K=1/ab, .
Part 3 Compelte Gabor filter form:
我们将公式8和公式6合并在一起,就得到了:
------------------------------------------------------ 9
我们再把公式1贴过来:
--------------------------- 10
比较两个公式,我们发现两者之间有些许的区别,我们找出之间的关联:
波长与频率关系:.那么两个公式不同的地方呢,开头和结尾,公式9的开头有系数,结尾还有指数常数项。
而这也是导致出现不同版本Gabor程序的原因所在。
Part4 多尺度和多方向
对于多尺度和多方向,就是要对公式9进行细化:
这样,就可以得到一组多尺度多方向的滤波器组了:
=========================程序部分===========================================
程序部分主要涉及的就是参数问题,因为随着Gabor的大规模应用,人们对参数进行了简化或者采用一些默认值。
比如在链接:http://blog.csdn.net/watkinsong/article/details/7882443 中,第三,四种实现方式就对应着公式2,而我再这里想重点介绍第五种实现方式,首先先介绍一下
这种方式对应的Gabor filter的函数形式:
其中:
于是多尺度和多方向就可轻松搞定了。这个就是第五种实现方式的原理,个人感觉这种方式才是最正宗的方式。
Reference:
[1]http://blog.csdn.net/watkinsong/article/details/7859185
---------------------
作者:Kevein111
来源:CSDN
原文:https://blog.csdn.net/carrierlxksuper/article/details/47189713
版权声明:本文为博主原创文章,转载请附上博文链接!