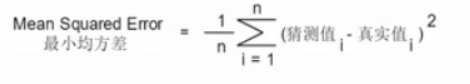• <人工智能>人工智能基础

    问题1：扔下圆球的位置（feature特征变量）变化，最终掉落奖项（label结果标签）的变化

    • feature ----输入
    • f(x) ----模型，算法
    • label ----输出

    　　大量已知的数据，训练得出f(x)

    • 一般的三步
      • 收集数据feature,label
      • 选择数据模型建立feature,label的关系--f(x)
      • 根据选择的模型进行预测　
    • 人类建立模型：多次尝试增加经验提高预测到达公司的时间
    • 机器学习：利用统计学，概率论，信息论的数学方法，利用已知的数据，创建一种模型，利用这种模型进行预测（高考与之类似）
      • 机器学习经典模型：KNN模型（人以类聚，物以群分）
        • 基本步骤　　
          • 1.采集数据
          • 2.计算实验数据与预测位置的距离
          • 3.按照距离从小到大排序
          • 4.选取最顶部的K条记录，得到最大概率的落点
          • 5.预测预测位置的落点
        • python实现 
          • import numpy as np
import collections as c
# 1.采集数据
data = np.array([
	[154, 1],
	[126, 2],
	[70, 2],
	[196, 2],
	[161, 2],
	[371, 4],
])

# feature,label
feature = data[:, 0]
label = data[:, -1]

# 2.计算实验数据与预测点的距离
predictPoint = 200
distance = list(map(lambda x: abs(x - predictPoint), feature))

# 3.按照距离从小到大排序,排序下标
sortindex = np.argsort(distance)


# 4.选取最顶部的K条记录，得到最大概率的落点,假设K=3
sortedlabel = label[sortindex]
k = 3
# 预测结果[(结果，次数)]
# 5.预测预测位置的落点
predictlabel = c.Counter(sortedlabel[0:k]).most_common(1)[0][0]

print(predictlabel)
        • 代码封装 
          • import numpy as np
import collections as c


# 代码封装

def knn(k, predictPoint, feature, label):
	distance = list(map(lambda x: abs(x - predictPoint), feature))
	sortindex = np.argsort(distance)
	sortedlabel = label[sortindex]
	predictlabel = c.Counter(sortedlabel[0:k]).most_common(1)[0][0]
	return predictlabel


if __name__ == '__main__':
	data = np.array([
		[154, 1],
		[126, 2],
		[70, 2],
		[196, 2],
		[161, 2],
		[371, 4],
	])
	# feature,label
	feature = data[:, 0]
	label = data[:, -1]
	k = 3
	predictPoint = 200
	res = knn(k, predictPoint, feature, label)
	print(res)
        • 实际数据验证
          • 数据集https://pan.baidu.com/s/1rw5aFlVzZb6SBdY09Rckhg
          • import numpy as np
import collections as c


# 代码封装

def knn(k, predictPoint, feature, label):
	distance = list(map(lambda x: abs(x - predictPoint), feature))
	sortindex = np.argsort(distance)
	sortedlabel = label[sortindex]
	predictlabel = c.Counter(sortedlabel[0:k]).most_common(1)[0][0]
	return predictlabel


if __name__ == '__main__':
	data = np.loadtxt("数据集/data0.csv", delimiter=",")
	# feature,label
	feature = data[:, 0]
	label = data[:, -1]
	k = 3
	predictPoint = 300
	res = knn(k, predictPoint, feature, label)
	print(res)
          训练集和测试集
          • 打散数据得到训练集和测试集
          • import numpy as np
          • import collections as c


# 代码封装

def knn(k, predictPoint, feature, label):
	distance = list(map(lambda x: abs(x - predictPoint), feature))
	sortindex = np.argsort(distance)
	sortedlabel = label[sortindex]
	predictlabel = c.Counter(sortedlabel[0:k]).most_common(1)[0][0]
	return predictlabel


if __name__ == '__main__':
	data = np.loadtxt("数据集/data0.csv", delimiter=",")
	# 打散数据
	np.random.shuffle(data)
	# 训练90%
	traindata = data[100:-1]
	# 测试10%
	testdata = data[0:100]
	# 保存训练数据,测试数据
	np.savetxt("data0-test.csv", testdata, delimiter=",", fmt="%d")
	np.savetxt("data0-train.csv", traindata, delimiter=",", fmt="%d")

	traindata = np.loadtxt("data0-train.csv", delimiter=",")

	# feature,label
	feature = traindata[:, 0]
	label = traindata[:, -1]
	max_accuracy = 0
	max_k = []
	# 预测点，来自测试数据的每一条记录
	testdata = np.loadtxt("data0-test.csv", delimiter=",")
	for k in range(1,100):
		count = 0
		for item in testdata:
			predict = knn(k, item[0], feature, label)
			real = item[1]
			if predict == real:
				count += 1

		accuracy = count * 100.0 / len(testdata)
		if accuracy >= max_accuracy:
			max_accuracy = accuracy
			max_k.append(k)
		print("k = {},准确率：{}%".format(k,count*100.0/len(testdata)))
	print(set(max_k))　

        • 多维数据的距离的选取

          • 欧式距离即可

        • 预测不是很准确
          • 1.模型的参数选择不够好，调参---调参工程师
            • K选择太小，噪音干扰太明显
            • K选择太大，其他类型的会涵盖　
            • K值的评价标准
              • 训练集trainData---得到模型
              • 测试集testData---验证模型　
            • 经验：K一般选取样本集开平方　　　　
          • 2.影响因子不够多
            • 增加数据的维度
              • 球的颜色导致弹性不同
              • 特殊数据的导入 
                • import numpy as np

def colornum(str):
	dict = {"红":0.50,"黄":0.51,"蓝":0.52,"绿":0.53,"紫":0.54,"粉":0.55}
	return dict[str]


data = np.loadtxt('数据集/data1.csv',delimiter=",",converters={1:colornum},encoding="gbk")
print(data)
          • 3.样本数据量不够
          • 4.选择的模型不够好，选择其他机器学习的模型　　　
      • 线性回归　　
        • 是一种总结规律，总结模型的解决方法。不需要全数据集
        • 损失函数：评测算法的好坏
        • 最小均方差　
        • 最小均方差越接近0越好
        • 步骤
          • 1.随机选取m和b
          • 2.分别计算m和b的偏导数
          • 3.如果m和b的偏导都很小，就成功
          • 4.根据学习速率，计算出修改的值
          • 5.b和m分别减去要修改的值　　
        • python实import numpy as np
        • # data = np.array([
# 	[80, 200],
# 	[95, 230],
# 	[104, 245],
# 	[112, 274],
# 	[125, 259],
# 	[135, 262],
# ])

data = np.loadtxt('数据集/cars.csv', delimiter=",", skiprows=1, usecols=(4, 1))

m = 1
b = 1

xarray = data[:, 0]
yreal = data[:, -1]
learningrate = 0.00001


# 梯度下降
def grandentdecent():
	# 求斜率
	bslop = 0
	for index, x in enumerate(xarray):
		bslop = bslop + m * x + b - yreal[index]
	bslop = bslop * 2 / len(xarray)
	# print("对b求导的斜率={}".format(bslop))

	mslop = 0
	for index, x in enumerate(xarray):
		mslop = mslop + (m * x + b - yreal[index]) * x
	mslop = mslop * 2 / len(xarray)
	# print("对m求导的斜率={}".format(mslop))

	return (bslop, mslop)


def train():
	for i in range(1, 10000000):
		bslop, mslop = grandentdecent()
		global m
		m = m - mslop * learningrate
		global b
		b = b - bslop * learningrate
		if (abs(mslop) < 0.5 and abs(bslop) < 0.5):
			break

	print("m={},b={}".format(m, b))


if __name__ == '__main__':
	train()

	# 用训练集得到公式
	# 用测试集验证正确率
        • import numpy as np

# 面积，房价
data = np.array([
	[80, 200],
	[95, 230],
	[104, 245],
	[112, 274],
	[125, 259],
	[135, 262],
])
# 1.feature,label,axis=1保留原始维度
feature = np.expand_dims(data[:, 0], axis=1)
# feature = data[:,0:1]
label = np.expand_dims(data[:, -1], axis=1)

# 2.weight
m = 1
b = 1

weight = np.array([
	[m],
	[b],
])
# 3.feature*weight,需要在feature后面补一列1---每一行代表mx+b
feature = np.append(feature, np.ones(shape=(6, 1)), axis=1)

print(feature)
# 4.feature*weight - label  得到差值difference
difference = np.dot(feature, weight) - label
# 5.feature^T*difference/n 先将feature转置在乘，得到对B和M的偏导bslop,mslop
bmslop = np.dot(feature.T, difference)
bmslop = bmslop*2/len(feature)
# 6.仅需使其数字接近0即可　　　　　　　　 

      • 图形变化

        • import matplotlib.pyplot as plt
import numpy as np
import math

points = np.array([
	[0, 0],
	[0, 5],
	[3, 5],
	[3, 4],
	[1, 4],
	[1, 3],
	[2, 3],
	[2, 2],
	[1, 2],
	[1, 0],
	[0, 0],
])
plt.plot(points[:, 0], points[:, 1])
for i in range(1,13):
	# # 1.平移
	# matrix = np.array([0.5*i, 0])
	# newpoints = points + matrix
	# 2.旋转
	# matrix = np.array([
	# 	[math.cos(math.pi/6),-math.sin(math.pi/6)],
	# 	[math.sin(math.pi/6),math.cos(math.pi/6)],
	# ])
	# points = np.dot(points,matrix)
	# 3.缩放
	matrix = np.array([
		[1.05,0],
		[0,1.05],
	])
	points = np.dot(points, matrix)
	plt.plot(points[:, 0], points[:, 1])
	plt.xlim(-10,10)
	plt.ylim(-10,10)
	plt.show()　　

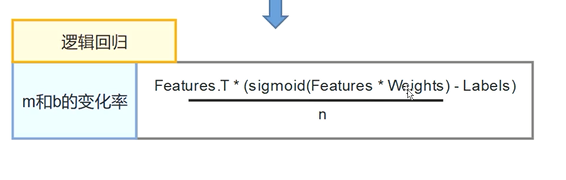
      • 逻辑回归

        • 将线性回归置于e的指数即可

        • e的求法

          • import math

n = 1000000

e = math.pow((1+1.0/n),n)

print(e)

        • 激活函数，sigmoid　

          • 逻辑回归实现梯度下降

            • import numpy as np

data = np.array([
	[5, 0],
	[15, 0],
	[25, 1],
	[35, 1],
	[45, 1],
	[55, 1],
])

# 1.feature,label,axis=1保留原始维度
feature = np.expand_dims(data[:, 0], axis=1)
# feature = data[:,0:1]
label = np.expand_dims(data[:, -1], axis=1)

learingrate = 0.00001
m = 1
b = 1

weight = np.array([
	[m],
	[b],
])

feature = np.append(feature, np.ones(shape=(6, 1)), axis=1)


def gradentDecent():
	predict = 1 / (1 + np.exp(-np.dot(feature, weight)))
	difference = predict - label
	bmslop = np.dot(feature.T, difference)
	bmslop = bmslop / len(feature)
	return bmslop


def train():
	for i in range(1, 10):
		slop = gradentDecent()
		global weight
		weight = weight - learingrate * slop
		print(slop)


if __name__ == '__main__':
	train()

      • 神经网络：主要用于分类和聚类

        • 用一条线划分两种类型的属性---分割线计算

        • 高维空间，只是变成了矩阵相乘---用面分割

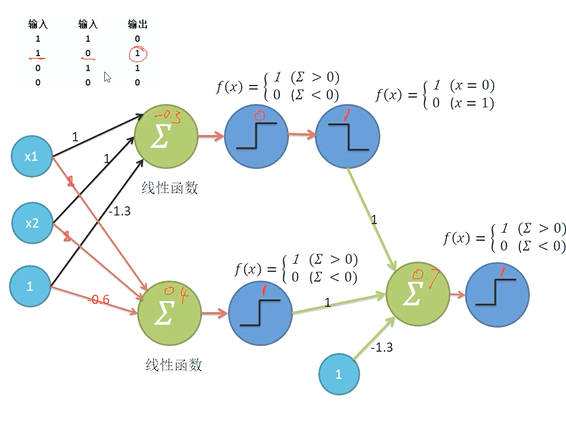
        • 神经元=激活函数=f(x)

        • 手工拟合OR，AND，XOR 

        • 感知机：梯度下降实现

          • 随便划线，感知点的情绪（- -），向着开心的方向进行移动

          • 调整线的斜率，使结果更好　　

          • 梯度下降：连续可导，可以求斜率

          • MSE最小均方差

          • Cross-entropy交叉熵

            • p(red)=p(blue)

            • sigmoid函数处理线性函数，　　　　

    • 聚类算法

      • 相似的事务归为一类-标签化---物以类聚

      • k-means

        • k:中心点的个数，质心

        • means：求平均

        • 不断迭代，更新质心　

        • 步骤

          • 1.选择聚类的个数K

          • 2.生成K个聚类中心点

          • 3.计算所有样本点到聚类中心点的距离

          • 4.更新质心(求聚类后的x,y平均值)，迭代聚类

          • 5.重复4直到满足收敛要求

          • import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans, KMeans
# 测量
from sklearn import metrics
# 球状簇
from sklearn.datasets.samples_generator import make_blobs

# 生成数据集，样本数=1000，特征数=2，中心=以哪些点为中心生成样本点,标准差=围绕中心的标准差，随机状态值=每次运行生成散点图一致
x, y = make_blobs(n_samples=1000, n_features=2, centers=([-1, -1], [0, 0], [1, 1], [2, 2]),
				  cluster_std=(0.4, 0.2, 0.2, 0.2), random_state=9)
# 生成散点图
plt.scatter(x[:, 0], x[:, 1], marker="o")
plt.show()

# 可视化
for index, k in enumerate((2, 3, 4, 5)):
	plt.subplot(2, 2, index + 1)
	# 随机选取200个点，分别用特征2,3,4,5作为特征值，进行K——means
	y_pred = MiniBatchKMeans(n_clusters=k, batch_size=200, random_state=9).fit_predict(x)
	# 聚类效果评分
	score = metrics.calinski_harabaz_score(x, y_pred)
	plt.scatter(x[:, 0], x[:, 1], c=y_pred)
	plt.text(.99,.01,
			 ('k=%d,score:%.2f' % (k, score)),
			 fontsize=10,
			 transform=plt.gca().transAxes,
			 horizontalalignment="right")
plt.show()

        • 　　　

        • 完整的预处理例子

          • '''
完整的机器学习流程
'''

# 1.导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy.random as nr
import math
from sklearn.cluster import MiniBatchKMeans, KMeans
# 测量
from sklearn import metrics
# 球状簇
from sklearn.datasets.samples_generator import make_blobs


# 2.观察数据集
# 路径带中文，前面先用open打开
auto_prices = pd.read_csv(open('工业汽车数据集应用实践/Automobile price data _Raw_.csv'))
# print(auto_prices.head(20))

# 3.数据的预处理，重新编码
auto_prices.columns = (str.replace('-', '_') for str in auto_prices.columns)

# 4.处理缺失值
# 找出所有缺失值
(auto_prices.astype(np.object) == '?').any()

for col in auto_prices.columns:
	if auto_prices[col].dtypes == object:
		count = 0
		count = [count + 1 for x in auto_prices[col] if x == '?']
		print(col + '	' + str(sum(count)))

# 处理缺失值
auto_prices.drop('normalized_losses', axis=1, inplace=True)
cols = ['price', 'bore', 'stroke', 'horsepower', 'peak_rpm']
for column in cols:
	auto_prices.loc[auto_prices[column] == '?', column] = np.nan
auto_prices.dropna(axis=0, inplace=True)
print(auto_prices.shape)

# 5.转换列数据类型
for column in cols:
	auto_prices[column] = pd.to_numeric(auto_prices[column])
print(auto_prices[cols].dtypes)

# 6.特征工程
# 汇总变量类别，转换ln,交互的变量合并
# 聚合特征变量
print(auto_prices['num_of_cylinders'].value_counts())
# print(auto_prices.columns)

cylinder_categories = {
	'three': 'three_four',
	'four': 'three_four',
	'five': 'five_six',
	'six': 'five_six',
	'eight': 'eight_twelve',
	'twelve': 'eight_twelve', }
auto_prices['num_of_cylinders'] = [cylinder_categories[x] for x in auto_prices['num_of_cylinders']]
print(auto_prices['num_of_cylinders'].value_counts())


# 7.箱型图
# 哪个特征影响价格走向
def plot_box(auto_price, col, col_y='price'):
	sns.set_style('whitegrid')
	sns.boxplot(col, col_y, data=auto_price)
	plt.xlabel(col)
	plt.ylabel(col_y)
	plt.show()


plot_box(auto_prices, 'num_of_cylinders')

print(auto_prices['body_style'].value_counts())
body_cats = {
	'sedan': 'sedan',
	'hatchback': 'hatchback',
	'wagon': 'wagon',
	'hardtop': 'hardtop_convert',
	'convertible': 'hardtop_convert', }
auto_prices['body_style'] = [body_cats[x] for x in auto_prices['body_style']]
print(auto_prices['body_style'].value_counts())


# 8.特征图
# 哪个特征有别于其他特征
def plot_box(auto_price, col, col_y='price'):
	sns.set_style('whitegrid')
	sns.boxplot(col, col_y, data=auto_price)
	plt.xlabel(col)
	plt.ylabel(col_y)
	plt.show()


plot_box(auto_prices, 'body_style')


# 9.转换变量
def hist_plot(vals, lab):
	sns.distplot(vals)
	plt.title('Histogram of' + lab)
	plt.xlabel('value')
	plt.ylabel('Density')
	plt.show()


hist_plot(auto_prices['price'], 'prices')
# 对数转换
auto_prices['log_price'] = np.log(auto_prices['price'])
hist_plot(auto_prices['log_price'], 'log_price')


# 10.可视化
# 看价格与其他特征是否存在线性或非线性的关系
def plot_scatter_shape(auto_prices, cols, shape_col='fuel_type', col_y='log_price', alpha=0.2):
	shapes = ['+', 'o', 's', 'x', '^']
	unique_cats = auto_prices[shape_col].unique()
	for col in cols:
		sns.set_style('whitegrid')
		for i, cat in enumerate(unique_cats):
			temp = auto_prices[auto_prices[shape_col] == cat]
			sns.regplot(col, col_y, data=temp, marker=shapes[i], label=cat,
						scatter_kws={'alpha': alpha}, fit_reg=False, color='blue')

		plt.title('scatter plot of' + col_y + 'vs.' + col)
		plt.xlabel(col)
		plt.ylabel(col_y)
		plt.legend()
		plt.show()


num_cols = ['curb_weight', 'engine_size', 'horsepower', 'city_mpg']
plot_scatter_shape(auto_prices, num_cols)

      • 算法效果的衡量标准

        • SSE（Sum of Squear due to Error）误差平方和

          • 每个点跟质心的距离　　

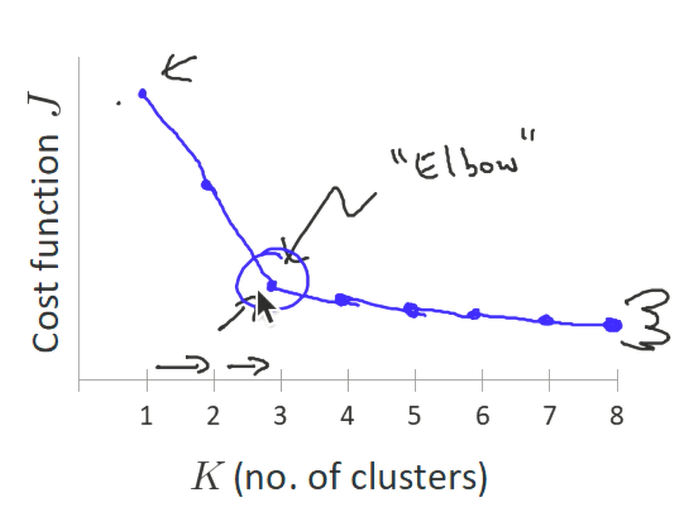
        • K值确定：Elbow method 肘方法

          • SSE跟聚类个数画图
          • 找出拐点来确定聚类数　　
          • 　　　　　　　　
        • 轮廓系数法（Silhouette Coefficient）
          • 根据轮廓边缘的变化感知聚类的凝聚度和分离度
          • 　　

        • CH（Calinski-Harabasz）

          • 数据类别距离平方和越小越好，类别之间平方和越大越好

          • 　　　　　　　　　　　　　　　　　　

            　　　　　　

     　　
  • 相关阅读:
    Oracle 验证A表的2个字段组合不在B表2个字段组合里的数据
    jQuery方法一览
    Maven构建项目时index.jsp文件报错
    ＤＤＬ——对数据库表的结构进行操作的练习
    不经意的小错误——onclick和click的区别
    UML基础——统一建模语言简介
    基于UML的面向对象分析与设计
    数据结构之——树与二叉树
    UML类图几种关系的总结
    C3P0连接参数解释
  • 原文地址：https://www.cnblogs.com/shuimohei/p/12052321.html
Copyright © 2020-2023  润新知