<数据可视化>Matplotlib（2D+3D）

1.Matplotlib介绍(2D)

　　Matplotlib 是 Python 2D-绘图领域使用最广泛的套件。它能让使用者很轻松地将数据图形化，并且提供多样化的输出格式。

　　pylab 是 matplotlib 面向对象绘图库的一个接口。

　　pylab模块里面集成了matplotlib和numpy，也可以导入pylab模块。
　　模块导入：

import numpy as np
import matplotlib.pyplot as plt

　　或者

from pylab import *

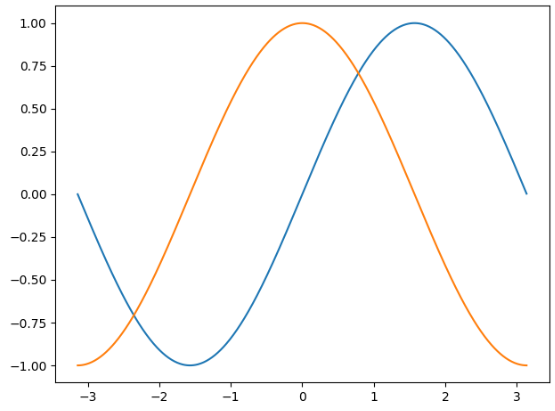
1.1 简单的例子

from pylab import *
# 生成一个数组，类似range
a = np.arange(1,9,1)
# 例子1：正弦和余弦函数
# np.pi就是π，x→[-π，π]，步长0.01
x = np.arange(-np.pi,np.pi,0.01)
y = np.sin(x)
y1 = np.cos(x)
plt.plot(x,y)
plt.plot(x,y1)
plt.show()

还有一种X的写法：

# endpoint:True一定包括终点，False不包括终点；x→[-π，π]，生成256个值，包括终点
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)

图形如下

1.2  默认配置的内容

# 导入 matplotlib 的所有内容（nympy 可以用 np 这个名字来使用）
from pylab import *

# 创建一个 8 * 6 点（point）的图，并设置分辨率为 80
figure(figsize=(8,6), dpi=80)

# 创建一个新的 1 * 1 的子图，接下来的图样绘制在其中的第 1 块（也是唯一的一块）
subplot(1,1,1)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

# 绘制余弦曲线，使用蓝色的、连续的、宽度为 1 （像素）的线条
plot(X, C, color="blue", linewidth=1.0, linestyle="-")

# 绘制正弦曲线，使用绿色的、连续的、宽度为 1 （像素）的线条
plot(X, S, color="green", linewidth=1.0, linestyle="-")

# 设置横轴的上下限
xlim(-4.0,4.0)

# 设置横轴记号
xticks(np.linspace(-4,4,9,endpoint=True))

# 设置纵轴的上下限
ylim(-1.0,1.0)

# 设置纵轴记号
yticks(np.linspace(-1,1,5,endpoint=True))

# 以分辨率 72 来保存图片
savefig("0001png",dpi=72)

# 在屏幕上显示
show()

图形如下：

　

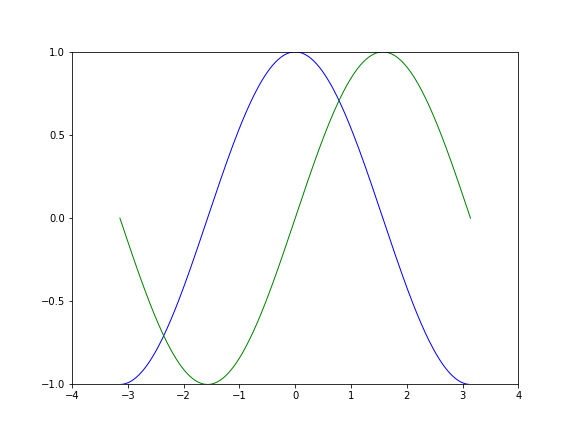
1.3 改变线条的颜色、粗细及图形的尺寸

from pylab import *
figure(figsize=(12,6), dpi=80)
x = np.arange(-np.pi,np.pi,0.01)
y = np.sin(x)
y1 = np.cos(x)
plt.plot(x,y,color="blue", linewidth=3.0, linestyle="-")
plt.plot(x,y1,color="red", linewidth=3.0, linestyle="-")
savefig("0001png",dpi=72)
plt.show()

图形为：

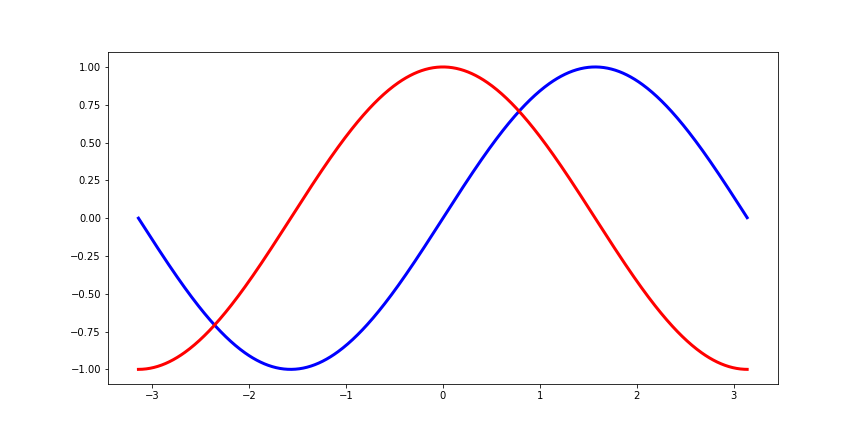
 1.4 设置图片边界

　　直接设定大小或等比例设定大小

# 设定坐标轴的上下限
xlim(-4.0, 4.0)
ylim(-1.0, 1.0)
# 按照具体的最大最小值设定上下限（这里设定为1.5倍）
xlim(x.min() * 1.5, x.max() * 1.5)
ylim(y.min() * 1.5, y.max() * 1.5)
# 通过差值的倍数去衡量更好
xmin, xmax = x.min(), x.max()
ymin, ymax = y.min(), y.max()

dx = (xmax - xmin) * 0.01
dy = (ymax - ymin) * 0.01　

图片为：

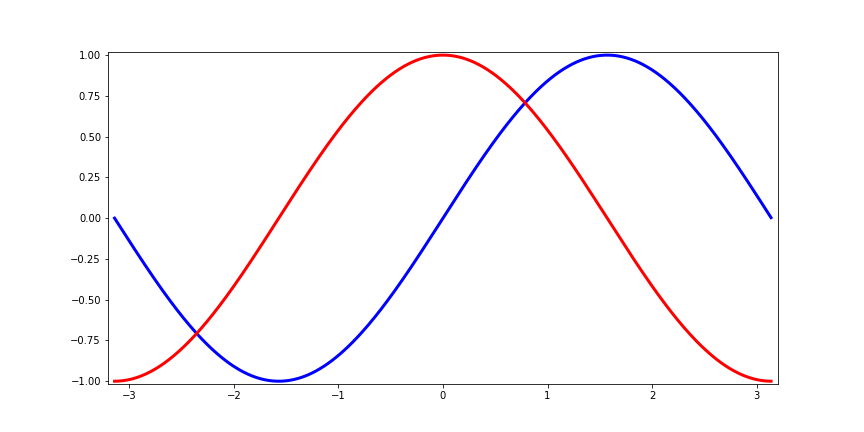
1.5 设置记号和对应的标签

# 记号-π，-π/2,0,π/2,π;第二行的标签使用了LaTeX（类似于HTML,长于写公式）
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-pi$', r'$-pi/2$', r'$0$', r'$+pi/2$', r'$+pi$'])

yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

图像为：

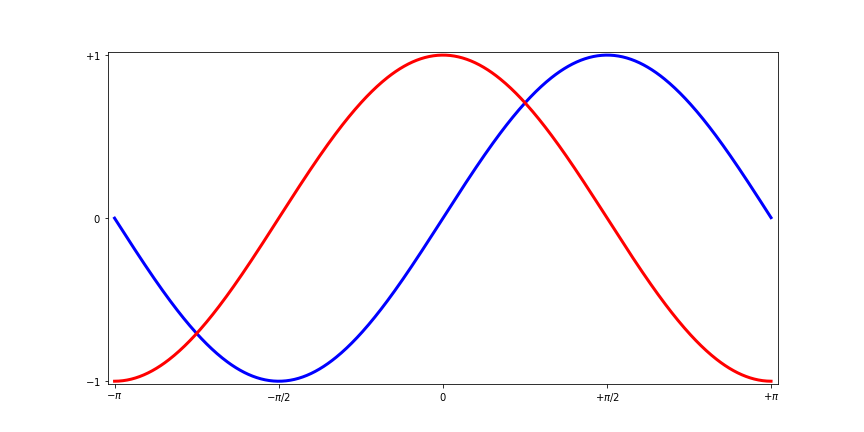
1.6 编写坐标轴

# 获取当前坐标轴对象
ax = gca()
# 一共有上下左右四条边框，设定2个边框为无色none,然后移动另外边框的位置，形成坐标轴
# 设定右边框为无色
ax.spines['right'].set_color('none')
# 设定上边框为无色
ax.spines['top'].set_color('none')
# 将水平坐标的刻度置于底边框（X轴下边）
ax.xaxis.set_ticks_position('bottom')
# 以底边框为X轴，将其置于数据坐标的原点
ax.spines['bottom'].set_position(('data',0))
# 将垂直坐标的刻度置于左边框（Y轴左边）
ax.yaxis.set_ticks_position('left')
# 以左边框为Y轴，将其置于数据坐标的原点
ax.spines['left'].set_position(('data',0))

图像为：

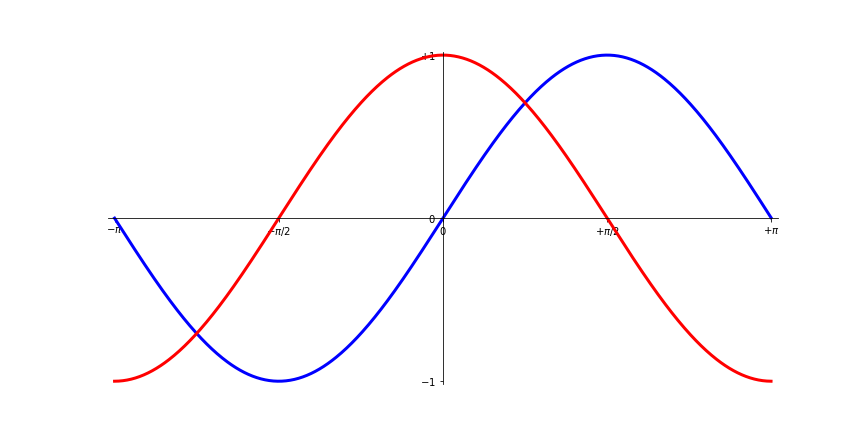
1.7  添加图例（小标签）

　　仅需要在画图的时候加一个label就行，类似：

plt.plot(x, y, color="blue", linewidth=3.0, linestyle="-",label="sin(x)")
plt.plot(x, y1, color="red", linewidth=3.0, linestyle="-",label="cos(x)")
plt.legend(loc=0)
# 跟上面作用一样
# legend(loc=0)
# legend(loc='upper left')

　　其中loc的值对应图例的位置，对应关系如下表：

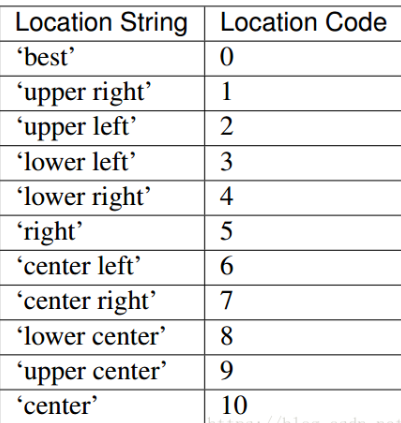
图像为：

1.8 坐标轴描述（文字说明）

　　主要是没有用坐标轴的时候使用，作为X轴和Y轴的说明

# import matplotlib as mpl
# 正常显示中文
mpl.rcParams['font.sans-serif']=['SimHei']
# 正常显示负数
mpl.rcParams['axes.unicode_minus']=False
# 添加X轴文字说明
plt.xlabel("abcdefg中文")
# 添加Y轴的文字说明
plt.ylabel("-1234567")

 图像为：

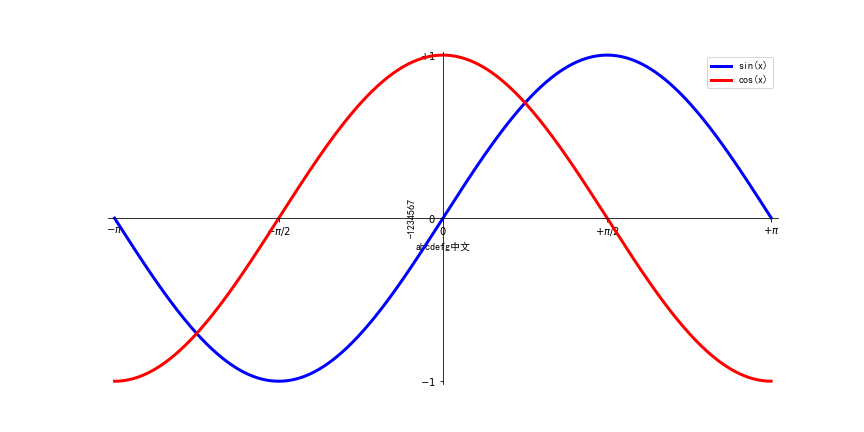
1.9 特殊点的标注（注释）

# annotate(注解，标注)，标注的文字，xy指箭头尖端位置[t，np.cos(t)],箭头的位置
# 文字的最左端的坐标（正数图像右边，负数图像左边），文字的位置，文字的大小
# 箭头类型
annotate(r'$cos(frac{2pi}{3})=frac{sqrt{3}}{2}$',
         xy=(t, np.cos(t)), xycoords='data',
         xytext=(-90, -50), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
# 同理
plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")
scatter([t,],[np.sin(t),], 50, color ='red')

annotate(r'$cos(frac{2pi}{3})=-frac{1}{2}$',
         xy=(t, np.sin(t)), xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

xycoords及textcoords的值：

| 参数 | 坐标系 | 
| 'figure points' | 距离图形左下角的点数量 | 
| 'figure pixels' | 距离图形左下角的像素数量 | 
| 'figure fraction' | 0,0 是图形左下角，1,1 是右上角 | 
| 'axes points' | 距离轴域左下角的点数量 | 
| 'axes pixels' | 距离轴域左下角的像素数量 | 
| 'axes fraction' | 0,0 是轴域左下角，1,1 是右上角 | 
| 'data' | 使用轴域数据坐标系 |

图像为：

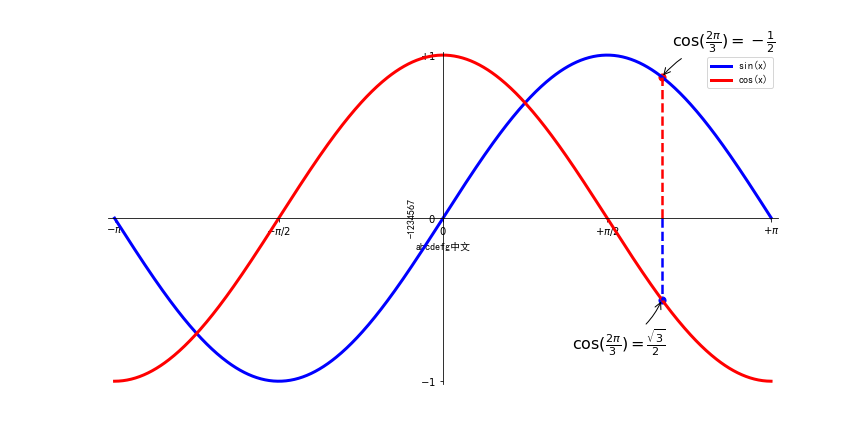
 1.10 显示坐标轴上被曲线挡住的标签

# 对于X和Y轴的的标签，设置大小为20，设置标签的底色，边框颜色，透明度
for label in ax.get_xticklabels() + ax.get_yticklabels():
    label.set_fontsize(20)
    label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.85))

图像为：

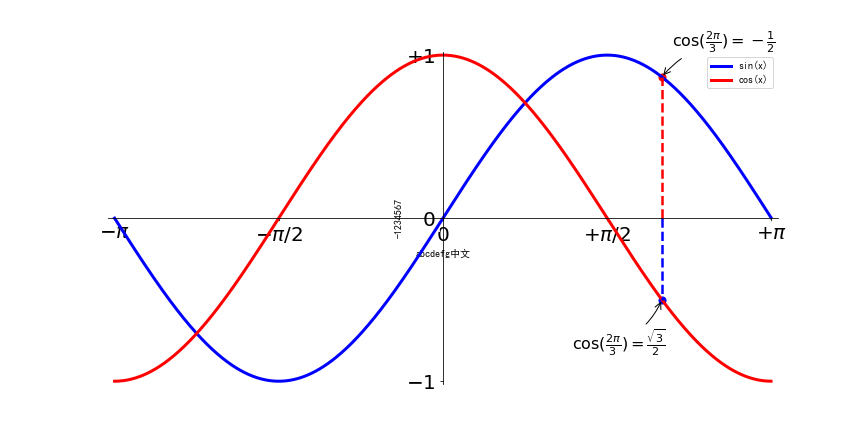
　　大小的改变实现了，挡住的标签貌似还是被挡住

1.11 子图的绘制

from pylab import *
# 两个子图的摆放
# (2,1,1) 分别代表：行数，列数，编号
plt.subplot(2, 1, 1)
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'subplot(2,1,1)', ha='center', va='center',
        size=20, alpha=.5)

plt.subplot(2, 1, 2)
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'subplot(2,1,2)', ha='center', va='center',
        size=20, alpha=.5)
# 自动调整子图参数，使之填充整个图像区域。它仅仅检查坐标轴标签、刻度标签以及标题的部分。
plt.tight_layout()
savefig("0002", dpi=72)
plt.show()

图像为：

以此类推：类似子图

另一种类型：

from pylab import *

import matplotlib.gridspec as gridspec

plt.figure(figsize=(18, 4))
# 设置三行三列
G = gridspec.GridSpec(3, 3)
# 第一行
axes_1 = plt.subplot(G[0, :])
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 1', ha='center', va='center', size=24, alpha=.5)
# 第二行第一个
axes_2 = plt.subplot(G[1:, 0])
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 2', ha='center', va='center', size=24, alpha=.5)
# 第二行最后一个
axes_3 = plt.subplot(G[1:, -1])
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 3', ha='center', va='center', size=24, alpha=.5)
# 第二行倒数第二个
axes_4 = plt.subplot(G[1, -2])
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 4', ha='center', va='center', size=24, alpha=.5)
# 最后一行（第三行）倒数第二个
axes_5 = plt.subplot(G[-1, -2])
plt.xticks(())
plt.yticks(())
plt.text(0.5, 0.5, 'Axes 5', ha='center', va='center', size=24, alpha=.5)
# 自动调整
plt.tight_layout()

savefig("0002", dpi=72)
plt.show()

图像为：

 

大图里面画小图（可以形成折叠效果）

from pylab import *

plt.figure(figsize=(8, 8))
# 最底下，初始位置（相对占比x,y），占据大小
plt.axes([.1, .1, .5, .5])
plt.xticks(())
plt.yticks(())
# 标签位置 内容等
plt.text(.5, .1, 'axes([0.1, 0.1, .5, .5])', ha='center', va='center',
		 size=20, alpha=.5)

# 倒数第二
plt.axes([.2, .2, .5, .5])
plt.xticks(())
plt.yticks(())
plt.text(.5, .1, 'axes([0.2, 0.2, .5, .5])', ha='center', va='center',
		 size=20, alpha=.5)
# 最上面
plt.axes([.3, .3, .5, .5])
plt.xticks(())
plt.yticks(())
plt.text(.5, .1, 'axes([0.3, 0.3, .5, .5])', ha='center', va='center',
		 size=16, alpha=.5)

plt.tight_layout()

savefig("0002", dpi=72)
plt.show()

　　

图像为：

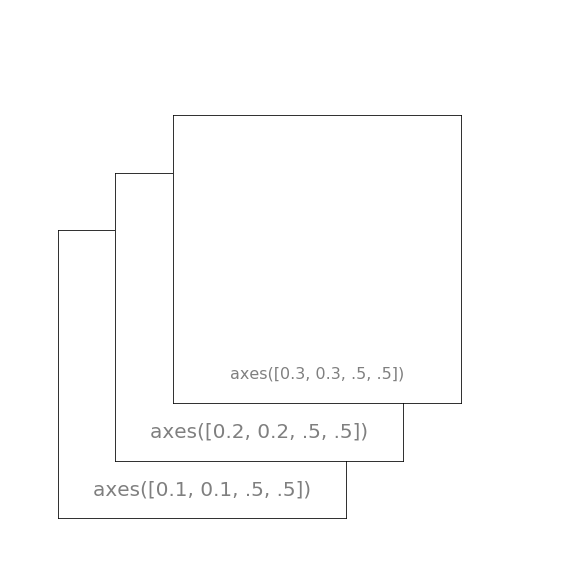
1.12 各种类型的2D图

普通图

from pylab import *

n = 256
X = np.linspace(-np.pi,np.pi,n,endpoint=True)
Y = np.sin(2*X)

plot (X, Y+1, color='blue', alpha=1.00)
plot (X, Y-1, color='blue', alpha=1.00)

savefig("0003", dpi=72)
plt.show()

图像为：

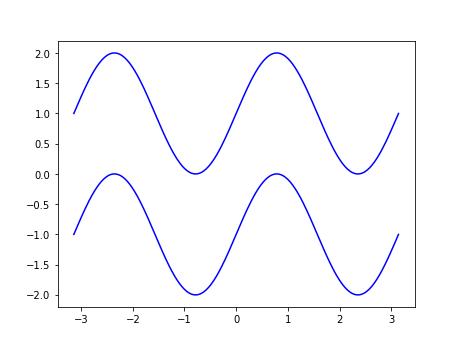
散点图

from pylab import *

n = 1024
X = np.random.normal(0,1,n)
Y = np.random.normal(0,1,n)

scatter(X,Y)

savefig("0003", dpi=72)
plt.show()

图像为：

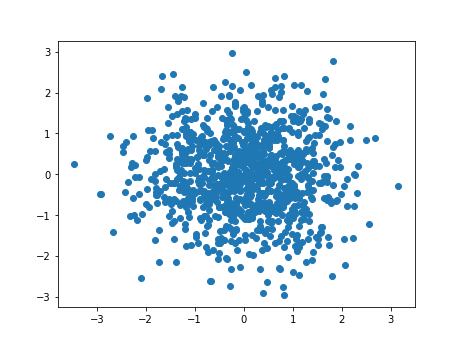
条形图

from pylab import *

n = 12
X = np.arange(n)
Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)

bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
bar(X, -Y2, facecolor='#ff9999', edgecolor='white')

for x,y in zip(X,Y1):
    text(x+0.05, y+0.05, '%.2f' % y, ha='center', va= 'bottom')

ylim(-1.25,+1.25)

savefig("0003", dpi=72)
plt.show()

图像为：

 

等高线图

from pylab import *


def f(x, y): return (1 - x / 2 + x ** 5 + y ** 3) * np.exp(-x ** 2 - y ** 2)


n = 256
x = np.linspace(-3, 3, n)
y = np.linspace(-3, 3, n)
X, Y = np.meshgrid(x, y)

contourf(X, Y, f(X, Y), 8, alpha=.75, cmap='jet')
C = contour(X, Y, f(X, Y), 8, colors='black', linewidth=.5)

savefig("0003", dpi=72)
plt.show()

图像为：

灰度图

from pylab import *


def f(x, y): return (1 - x / 2 + x ** 5 + y ** 3) * np.exp(-x ** 2 - y ** 2)


n = 10
x = np.linspace(-3, 3, 4 * n)
y = np.linspace(-3, 3, 3 * n)
X, Y = np.meshgrid(x, y)

imshow(f(X, Y))
savefig("0003", dpi=72)
plt.show()

　　

图像为：

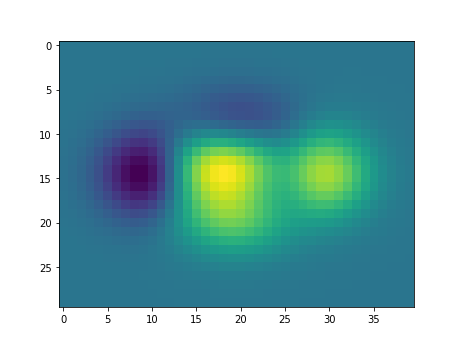
饼状图

from pylab import *

n = 20
Z = np.random.uniform(0,1,n)
pie(Z)
savefig("0003", dpi=72)
plt.show()

图像为：

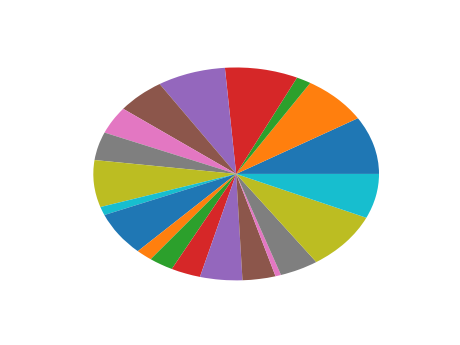
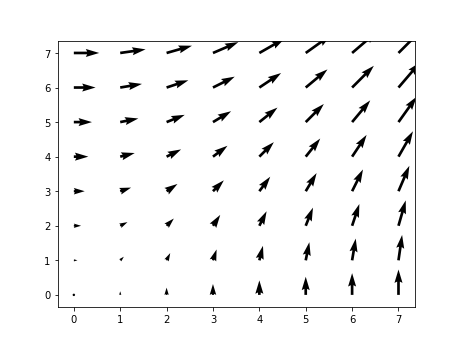
量场图

from pylab import *

n = 8
X,Y = np.mgrid[0:n,0:n]
quiver(X,Y)
savefig("0003", dpi=72)
plt.show()

图像为：　

2.Matplotlib介绍(3D)

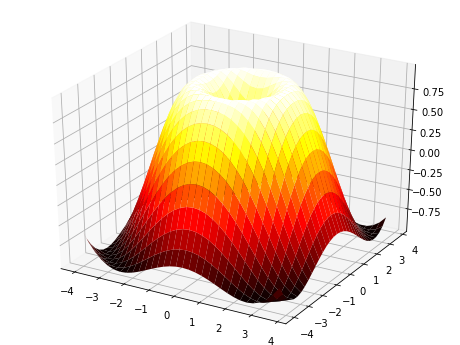
3D图

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot')

savefig("0003", dpi=72)
plt.show()

图像为：

2.1 3D图例子

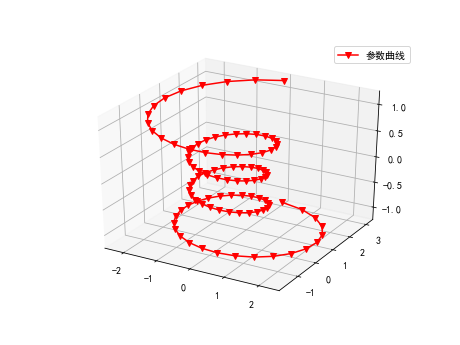
普通图3D系列

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

# 绘制三维图形
fig = plt.figure()
ax = fig.gca(projection="3d")

# 生成测试数据
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-4, 4, 100) * 0.3
r = z**4 +1
x = r*np.sin(theta)
y = r*np.cos(theta)

# 绘制三维曲线，标签
ax.plot(x,y,z,'rv-',label="参数曲线")

# 可以设置字体，字号，显示图例
mpl.rcParams['legend.fontsize'] = 10
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
ax.legend()
savefig("0003", dpi=72)
plt.show()

图像为：

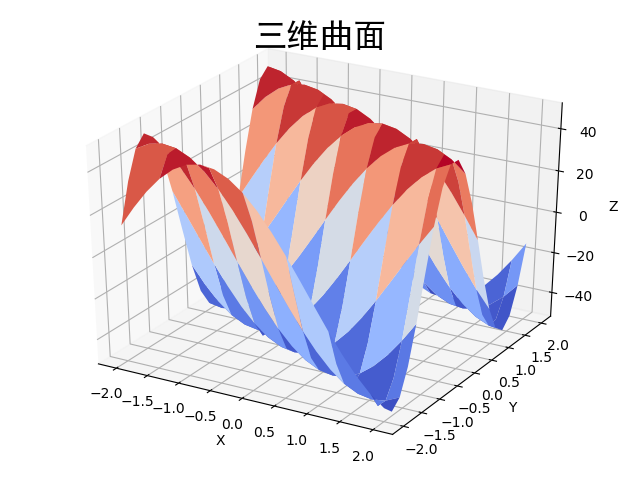
三维曲面

from pylab import *
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d
# 生成测试数据
x,y = np.mgrid[-2:2:20j,-2:2:20j]
z = 50 * np.sin(x+y*2)

# 创建三维图像
ax = plt.subplot(111,projection='3d')
# 绘制三维曲面
ax.plot_surface(
	x,y,z,
	rstride=3,cstride=2,
	cmap=plt.cm.coolwarm,
)
# 设置坐标轴标签
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# 设置图形标题
ax.set_title("三维曲面",fontproperties='simhei',fontsize=24)
plt.show()

　　图像为：

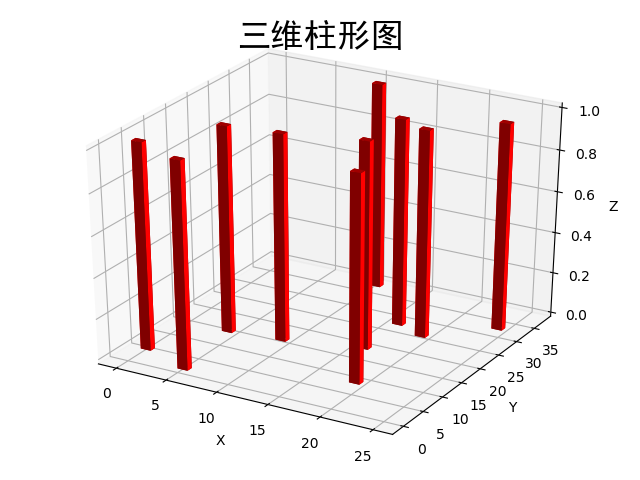
三维柱状图

from pylab import *
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d
# 生成测试数据
x = np.random.randint(0,40,10)
y = np.random.randint(0,40,10)
z = 80*abs(np.sin(x+y))
# 创建三维图像
ax = plt.subplot(111,projection='3d')
# 绘制三维曲面
ax.bar3d(
	x,y,
	np.zeros_like(z), #设置z的起始坐标为0
	dx =1,
	dy =1,
	dz =1, # x,y,z方向的宽度，厚度，高度
	color = 'red',
)
# 设置坐标轴标签
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# 设置图形标题
ax.set_title("三维柱形图",fontproperties='simhei',fontsize=24)
plt.show()

　　图像:

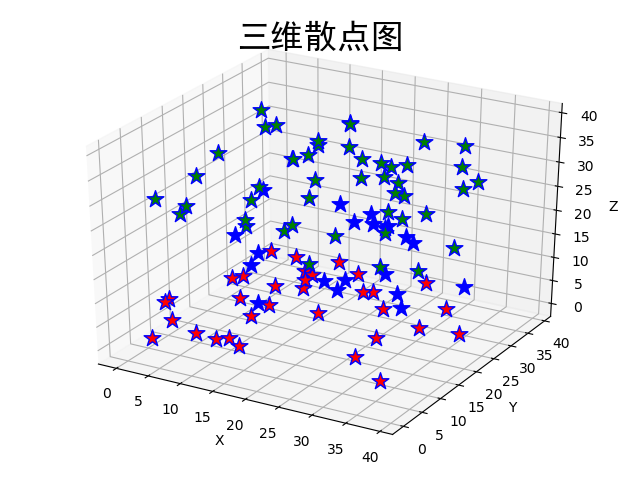
三维散点图

from pylab import *
from mpl_toolkits.mplot3d import Axes3D
import mpl_toolkits.mplot3d
# 生成测试数据
x = np.random.randint(0,40,100)
y = np.random.randint(0,40,100)
z = np.random.randint(0,40,100)

# 创建三维图像
ax = plt.subplot(projection='3d')
# 绘制三维散点
for xx,yy,zz in zip(x,y,z):
	color = 'r'
	if 10<zz<20:
		color='b'
	elif zz>=20:
		color='g'
	ax.scatter(xx,yy,zz,c=color,marker='*',
			   s=160,linewidths=1,edgecolor='b')
# 设置坐标轴标签
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# 设置图形标题
ax.set_title("三维散点图",fontproperties='simhei',fontsize=24)
plt.show()

图像为