本文参考:https://zhuanlan.zhihu.com/p/39762178
设 是一个函数,它的输入是向量
,输出是向量
:
那么雅可比矩阵是一个m×n矩阵:
由于矩阵描述了向量空间中的运动——变换,而雅可比矩阵看作是将点 转化到点
,或者说是从一个n维的欧式空间转换到m维的欧氏空间。
如果m = n, 可以定义雅可比矩阵 的行列式,也就是雅可比行列式(Jacobian determinant)。
在微积分换元中,也就是给出了 从x到y的n维体积的比率
2.二维雅可比矩阵的几何意义
在二维情况(有直观的图),雅可比行列式代表xy平面上的面积微元与uv平面上的面积微元的比值。
设 ,雅可比行列式是:
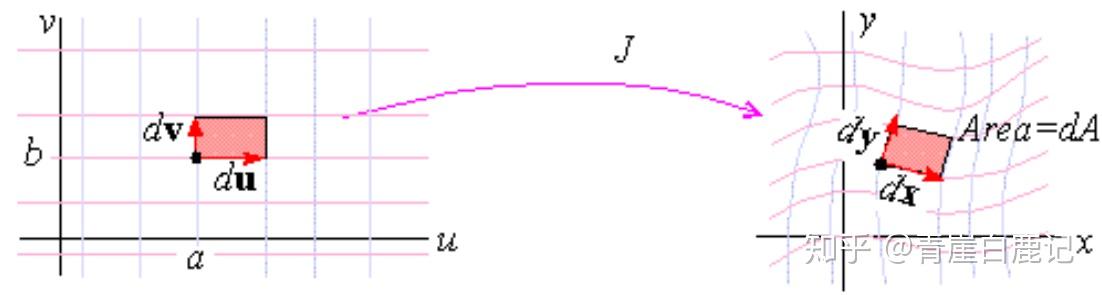
如图所示:dA代表dx和dy张成的平行四边形的面积,如果du和dv充分接近于0,那么dA:
二重积分换元:
n维情况以此类推。