逻辑回归-1.原理

逻辑回归

解决分类问题：将样本的特征和样本发生的的概率联系起来，逻辑回归既可以看作是分类算法，也可以看作回归算法

考虑之前的线性回归算法：$hat y = f(x) $ --> $ hat y = X_b cdot heta $ ,其中值域为：$ (-infty,+infty)$
对于概率来讲，它的值域为[0,1]，所以，需要将结果作为特征值传入$ sigma $函数：

[hat p = sigma (X_b cdot heta) ]

其中$ sigma $ 的表达式为：$ sigma (t)= frac{1}{1+e^{-t}} $

绘制$ sigma(t) $函数

import numpy
import matplotlib.pyplot as plt

def sigmoid(t):
    return 1/(1+numpy.exp(-t))
    
x = numpy.linspace(-10,10,500)
y = sigmoid(x)
plt.plot(x,y)
plt.show()

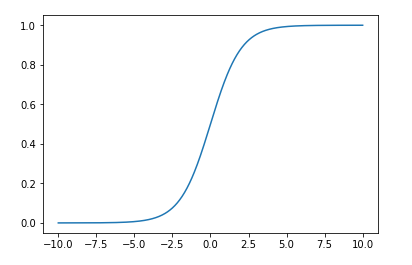
由上可以看出，函数将值域映射到[0,1]了，当t取0时，$ sigma $取0.5
逻辑回归结构：

逻辑回归的损失函数

如果y的真实分类值为1，而预测的p越大，损失越小，预测的p越小，损失越大
如果y的真实分类值为0，而预测的p越大，损失越大，预测的p越小，损失越小

由此特性，可以定义损失函数：

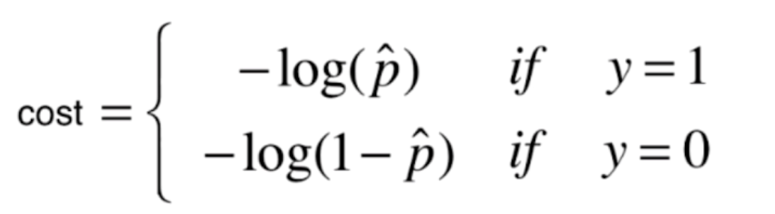
画出y=1时的损失函数：$ -log(hat p) $:

def log(t):
    return numpy.log(t)
    
p = numpy.linspace(0,1,500)
y1 = -log(p)
plt.plot(p,y1)
plt.show()

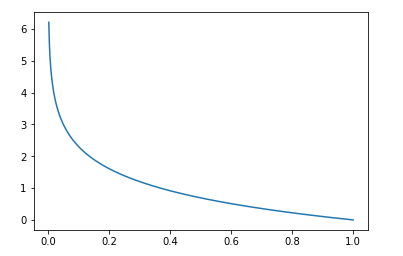
预测的概率p越大，准确率越高，损失值越小，当p为1时，准确率100%，损失为0
画出y=0时的损失函数：$ -log(1-hat p) $:

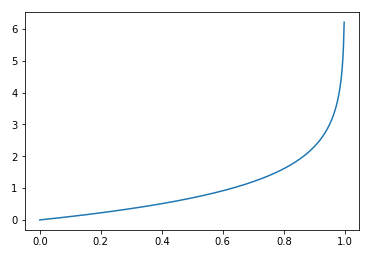
预测的概率p越大，准确率越低，损失值越大，当p为1时，准确率为0，损失无穷大

将上面损失函数合二为一：$ cost = -ylog(hat p)-(1-y)log(1-hat p) $

由此得出逻辑回归的损失函数：

[J( heta) = -frac{1}{m}sum_{i=1}^{m}y^{(i)}log(hat p^{(i)})+(1-y^{(i)})log(1-hat p^{(i)}) ]

其中：$ hat p^{(i)} = sigma ( heta^T cdot x_b) = frac{1}{1+e^{-X_b{(i)} cdot heta }} $