线性回归算法的实现
import numpy
import matplotlib.pyplot as plt
# 使用自己模拟的简单数据集
x = numpy.array([1,2,3,4,5])
y = numpy.array([1,3,2,3,5])
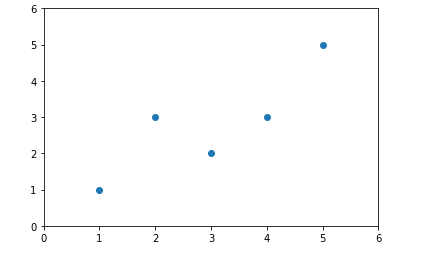
plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()
线性回归算法核心,求a,b的值:
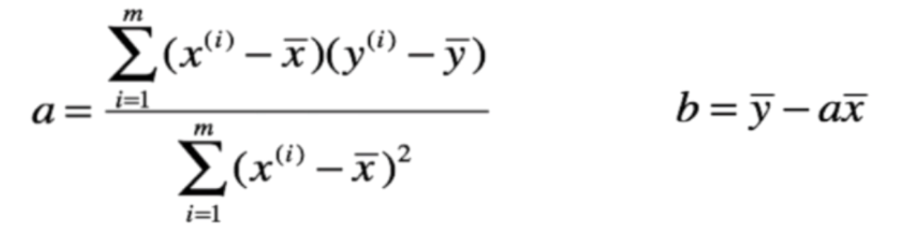
# 求数据集的平均数
x_mean = numpy.mean(x)
y_mean = numpy.mean(y)
# 求a和b的值
m = 0
z = 0
#此处计算效率太低,后续需要进行向量化
for x_i,y_i in zip(x,y):
z += (x_i-x_mean)*(y_i-y_mean)
m += (x_i-x_mean)**2
a = z/m
b = y_mean - a*x_mean

y_hat = a*x+b
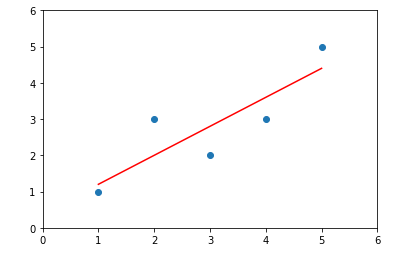
plt.scatter(x,y)
plt.plot(x,y_hat,color='r')
plt.axis([0,6,0,6])
plt.show()
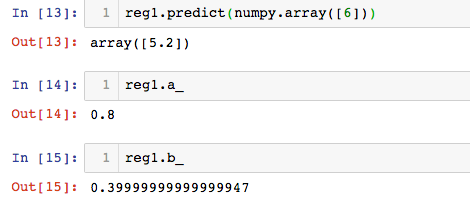
调用自己封装的库
调用SimpleLineRegression库
from mylib.SimpleLineRegression import SimpleLineRegression
reg1 = SimpleLineRegression()
reg1.fit(x,y)
reg1.predict(numpy.array([6]))
向量化
a值计算时采用for循环,效率较低,观察a的表达式发现,可以用向量间的点乘实现:
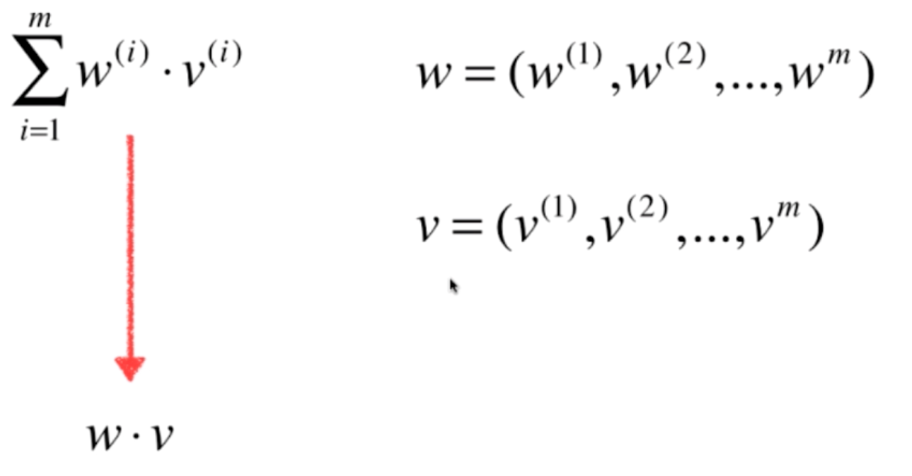
实现:
z = (x_train-x_mean).dot(y_train-y_mean)
m = (x_train-x_mean).dot(x_train-x_mean)
a = z/m
b = y_mean - a*x_mean
性能比较
# 用随机数生成100万个样本
m = 1000000
big_x = numpy.random.random(size=m)
# 模拟线性回归 a=2,b=3,构造y=ax+b,每个样本加入正态分布的干扰
big_y = 2.0*big_x + 3.0 + numpy.random.normal(size=m)
from mylib.SimpleLineRegression import SimpleLineRegression_1,SimpleLineRegression_2
reg1 = SimpleLineRegression_1()
reg2 = SimpleLineRegression_2()
%timeit reg1.fit(big_x,big_y) # for循环
%timeit reg2.fit(big_x,big_y) # 向量化
由下图可以看出,向量化运算比简单的for循环要快100倍
