uva 11538 (排列组合)
主要是推公式nP2 n为有多少个点可以选放两个皇后,行和列的公是显而易见
分别为 n*m*(m-1) and m*n*(n-1)主要是对角线的公式难出来。先分析一个4*7的棋盘
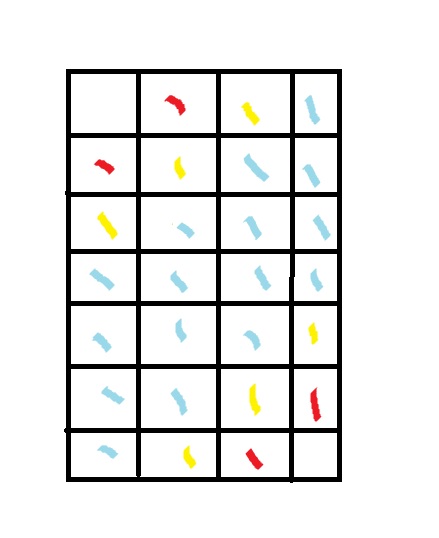
图上蓝色的均为有m个格子可以选对于这部分可以推出公是(n-m+1)*m*(m-1)
对于彩色的格子则可以看出他是从2-(n-1)的2*∑i*(i-1)
推出公式m*(m-1)*(2*m-4)/3然后就是编程求解了,代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #define ll long long 5 using namespace std; 6 7 //m<=n 8 inline ll solve(ll m, ll n) 9 { 10 ll row = m*n*(n-1), col = n*m*(m-1), dia = (n-m+1)*m*(m-1)+m*(m-1)*(2*m-4)/3; 11 return row+col+2*dia; 12 } 13 14 int main() 15 { 16 // freopen("in.txt", "r", stdin); 17 18 ll m, n; 19 while(scanf("%lld%lld", &m, &n)!=EOF) 20 { 21 if(n==0 && m==0)break; 22 ll ans = solve(min(m, n),max(m,n)); 23 printf("%lld ", ans); 24 } 25 return 0; 26 }
uva 11401 (简单递推)
从1-n中选出三个数组成三角形,有多少种不同的方案。
由于数据较大无法暴力,只能想递推公式了。ans[i]的意义是最长边长为i能有做少种方案。
ans[i] = ans[i-1]+c[i];
下面来讨论c[i]中包含哪些项 设三角形三边为a, b, i(最长边)有a+b>i
由于i固定枚举a可知道当a = 1,2,3,...,i-1时b的方案。正好得出b = 0,1,2...,i-2
这样可得出总的情况b = (i-1)*(i-2)/2但是这样计入了a==b的情况(方案数-(int)(n/2))
最后由于每种情况都计算了两遍所以直接除以二就是c[i]的正确值了。
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #define ll long long 6 #define maxn 1001000 7 using namespace std; 8 9 ll ans[maxn]; 10 11 void init() 12 { 13 ans[3] = 0; 14 for(ll i=4; i<1000001; i++){ 15 ans[i] = ans[i-1] + ((i-1)*(i-2)/2 - (i-1)/2)/2; 16 } 17 } 18 19 int main() 20 { 21 // freopen("in.txt", "r", stdin); 22 23 int n; 24 init(); 25 while(scanf("%d", &n)!=EOF){ 26 if(n<3)break; 27 printf("%lld ", ans[n]); 28 } 29 return 0; 30 }
uva 11806 (容斥原理)
很容易想到是容斥原理,但是WA了好多次一直在查原因查不出来,最后无奈用liurujia书上的代码一块块替换,刚换初始化时交上去就ac了。
接下来想了一下初始化哪里错了。一开始我初始化算C(nk)使用公式算的,而书上则使用的递推虽然复杂度一样但是仔细考虑一下发现问题出在了MOD上面。
一旦后一个阶乘足够大则会导致他与前面的阶乘除法出错。所以很无奈我这个初始化貌似不行,然后貌似我能想到的改进方法则是开二维数组初始化jc。这个貌似小题大作了。
还是应该把书上的学会。(我实在是太菜了!)
代码如下:

1 //Cheerleader.cpp 2 //容斥原理 3 #include <iostream> 4 #include <cstdio> 5 #include <cstring> 6 #define ll long long 7 #define MOD 1000007 8 using namespace std; 9 10 int T; 11 ll n, m, k, jc[2000], c[510][510]; 12 13 //一开始wa的初始化函数 14 //void init() 15 //{ 16 // jc[0] = 1; 17 // for(int i=1; i<1000; i++){ 18 // jc[i] = (jc[i-1]*i)%MOD; 19 // } 20 //} 21 22 //inline ll C(ll _n, ll _k) 23 //{ 24 // if(_k>_n) return 0; 25 // return (jc[_n]/(jc[_n-_k]*jc[_k]))%MOD; 26 //} 27 28 void init() 29 { 30 memset(c, 0, sizeof c); 31 c[0][0] = 1; 32 for(int i=0; i<510; i++){ 33 c[i][0] = c[i][i] = 1; 34 for(int j=1; j<i; j++){ 35 c[i][j] = (c[i-1][j]+c[i-1][j-1])%MOD; 36 } 37 } 38 } 39 40 inline ll C(ll _n, ll _k){return c[_n][_k];} 41 42 ll solve() 43 { 44 ll ret = C(n*m,k); //总的情况 45 ret = ret + 4*MOD - 2*C((n-1)*m,k)-2*C((m-1)*n,k); //有一行或一列不选 46 ret %= MOD; 47 ret = ret + 4*C((n-1)*(m-1),k) + C(n*(m-2),k) + C((n-2)*m,k); //两行或两列或一行一列不选 48 ret %= MOD; 49 ret = ret + 4*MOD - 2*C((n-1)*(m-2),k)-2*C((m-1)*(n-2),k); 50 ret %= MOD; 51 ret = ret + C((n-2)*(m-2),k); //两行两列都不选 52 ret %= MOD; 53 return ret; 54 } 55 56 int main() 57 { 58 // freopen("in.txt" ,"r", stdin); 59 60 init(); 61 scanf("%d", &T); 62 for(int cnt=1; cnt<=T; cnt++){ 63 scanf("%lld%lld%lld", &m, &n, &k); 64 ll ans = solve(); 65 printf("Case %d: %lld " ,cnt, ans); 66 } 67 return 0; 68 }
