上次我们学习了环形链表的数据结构,那么接下来我们来一起看看下面的问题,
判断一个单向链表是否是环形链表?
看到这个问题,有人就提出了进行遍历链表,记住第一元素,当我们遍历后元素再次出现则是说明是环形链表,如果没有这是一个单向非环形链表。
我们来分析下上述的解决方法,我们分析这个程序的时间复杂度则是O(n)。 那么是不是最优的选择呢?
我们引入新的解决思路,那就是“快慢指针”。 我们来看看接下来的解决思路,是否比上面的思路有优化的地方。
思路: 当我们在遍历链表的时候,我们设计两个指针,分别是快指针和慢指针,块指针每次走2步,而慢指针每次走1步,这样的话在当我们两个指针在链表中,如果会第二次相遇则说明这里面的链表是环形链表。
我们来用代码实现
|
/** * 查看 链表中是否存在环形 * * @return */ public boolean hasRing() { if (head != null && size > 0) { Node<T> fastTemp = head, lowTemp = head; while (lowTemp.getNext() != null && fastTemp.getNext() != null) { fastTemp = fastTemp.getNext().getNext(); lowTemp = lowTemp.getNext(); if (lowTemp == fastTemp) { return true; } } } return false; } |
解析:定义了两个指针节点 分别是 Node<T> fastTemp = head, lowTemp = head;
分别都是从head 开始 移动。那么下一次项目的时候,则是快指针走了两圈,慢指针走了一圈,所一下次相遇在原地位置。
接下来的问题就是我们在设计快慢指针的时候,是否必须是2倍速速的快慢指针。
如图所示:
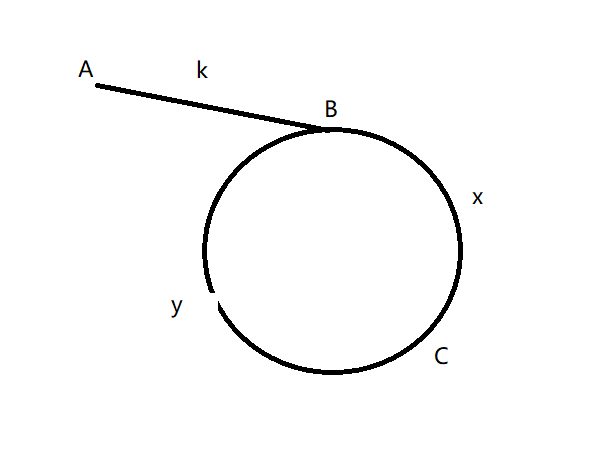
假设: 快慢指针在C点相遇,那么相遇点在离循环点B之间是x 那么头节点A离B的距离为 k
在相遇的时候
慢指针:K + X + n*(X+Y) = m; ①
X+Y 绕环一圈的距离;n 慢指针 总共绕了几圈在环内
快指针:
快指针是慢指针 速度的2倍,当它们相遇时 所用的时间是一样的。那么快指针 走过得距离是2*m;
K+X +N*(X+Y) = 2*m; ②
N为快指针绕过得圈数
将 ② - ① 得到下面公式
(N-n)*(X+Y) = m;
接下将 ① 代入 上式得到
(N-n)*(X+Y) = K+X+n*(X+Y);
这里X+Y 环长是个定值。 假设环长为M
(N-n)*M = K+X+n*M; ---- > 得出变形得到 K+X = (N-2*n)*M ;
公式 :K+X = (N-2*n)*M
由于我们设计的是O型循环链表,那么 起始就是循环点B上,则(N-2*n)*M = 0。
N = 2*n; 相遇时 快慢指针所绕 环的圈数 前者是后者的2倍,所用时间相同。这里跟环有多少节点没有关系。
上海尚学堂java培训原作,陆续有数据机构等等java技术文章奉上,请多关注!
下面看一个例子:
给定一个未知的长度的单向环形链表,如何确定链表中间位置的节点元素?
我们也可以使用“快慢指针”来实现,当快指针走一圈,然后停止,那么慢指针的位置则是,中间元素的位置。此时的 时间复杂O(n) = 1/2 n