想学ac自动机,发现要先学字典树,学了字典树,看到一道题是字典树和欧拉回路配合使用的(POJ2513)很有兴趣,来看看欧拉路径。
一、概念
欧拉路径:一条经过图G上每一条边(不是点)恰好一次的路径。(一笔画问题)
欧拉回路:起点和终点相同
二、存在前提
1.必然是一个连通图
2.如果是无向图,图上 奇数度数的 点的个数 必须是0或者2
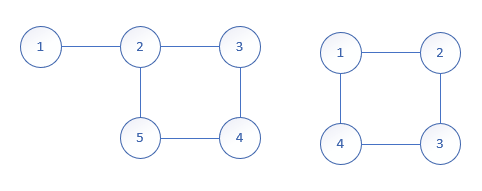
左图度数为奇数的点有1和2,个数为2
右图度数为奇数的点的个数为0(欧拉回路)
3.如果是有向图,则要么所有点的入度和出度一样,要么有两个点的入度分别比出度多1和少1
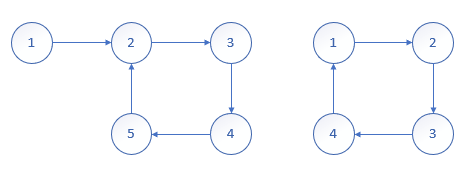
左图:1号点,入度为0,出度为1;2号点,入度为2,出度为1;其他入度和出度相同
右图:所有点入度和出度相同(欧拉回路)
三、证明
自己画一画,居然全对,那应该就是真的了
四、解题套路
一般用并查集和dfs,视情况而定,递归不熟练的还是用并查集稳点。dfs常用于输出字典序最小的欧拉路径。
五、例题
题目1:http://acm.hdu.edu.cn/showproblem.php?pid=1878
无向图判断是否存在欧拉回路,并查集+标记度数。(学到欧拉路径的人并查集肯定是会的)

#include<stdio.h> #include<iostream> #include<algorithm> #include<cstring> #include<math.h> #include<string> #define ll long long #define inf 0x3f3f3f3f using namespace std; int n,m; int par[10086]; int deg[10086]; void init() { memset(deg,0,sizeof(deg)); for(int i=1;i<=n;i++) par[i]=i; } int find(int x) { if(x!=par[x]) return par[x]=find(par[x]); else return x; } void unite(int x,int y) { int xx=find(x); int yy=find(y); if(xx!=yy) par[xx]=yy; } int main()///hdu1878 { while(scanf("%d",&n)!=EOF && n) { init(); scanf("%d",&m); for(int i=1;i<=m;i++) { int a,b; scanf("%d %d",&a,&b); unite(a,b); deg[a]++; deg[b]++; } int boss=find(1); int flag=true;///判断是否连通 以及 度数为奇数的点的个数为0 for(int i=1;i<=n;i++) { if(find(i)!=boss || deg[i]%2) { flag=false; break; } } if(flag) printf("1 "); else printf("0 "); } return 0; }
题目2:https://www.luogu.org/problem/P1341
判断将能否将许多个两个字母的字符串首位相接,要求字典序最小。也是欧拉路径的题目,这道题没上一道裸,不过后台数据很水,没有判断连不连通,代码最后加了一组不连通的数据。详看代码

#include<stdio.h> #include<iostream> #include<algorithm> #include<cstring> #include<math.h> #include<string> #include<vector> #define ll long long #define inf 0x3f3f3f3f using namespace std; struct node { int x; int idx;///边的下标,欧拉回路是数边 }; int n,cnt; char s[5];///A-Z=65-90 a-z=97-122; int deg[60];///A-Z=0-25 a-z=32-57 bool flag; string ans=""; vector<node>a[60]; bool vis[100005];///n大小也不知道是多少 bool cmp(node p1,node p2) { return p1.x<p2.x; } void dfs(int now,int num,string res)///当前点,当前遍历的边数,存储的答案 { if(flag) return; if(num==n) { flag=true;///第一次进来必然是num=n,即走完所有的边,随后进来都是因为找到第一个答案了 ans=res; return; } int len=a[now].size(); for(int i=0;i<len;i++) { int next=a[now][i].x; int id=a[now][i].idx; if(vis[id])///如果这条边走过,则跳过 continue; else { vis[id]=true; dfs(next,num+1,res+(char)(next+'A')); vis[id]=false; } } } int main()///P1341 { while(scanf("%d",&n)!=EOF && n) { memset(deg,0,sizeof(deg)); memset(vis,false,sizeof(vis)); for(int i=0;i<60;i++) a[i].clear(); for(int i=1;i<=n;i++) { scanf("%s",s); int x=s[0]-'A'; int y=s[1]-'A'; deg[x]++; deg[y]++; a[x].push_back({y,i}); a[y].push_back({x,i}); } for(int i=0;i<60;i++) sort(a[i].begin(),a[i].end(),cmp);///邻接表按顺序排,dfs第一次成功就能搜出字典树最小的 for(int i=0;i<60;i++) if(deg[i]%2) cnt++; if(cnt!=2 && cnt!=0)///两个度数为奇数的点作为起点和终点,否则无法形成一条字符串 { printf("No Solution "); continue; } int start=-1; for(int i=0;i<60;i++)///找到第1个字母 if(deg[i]) { start=i; break; } for(int i=0;i<60;i++)///如果不是回路,找到第一个入度为奇数的,当作起点;如果是回路则选择上面那个 if(deg[i]%2) { start=i; break; } ans=""; flag=false; string temp=""; temp+=(char)(start+'A'); dfs(start,0,temp); if(ans.size()) cout<<ans<<endl; else cout<<"No Solution "; } return 0; } /** 不连通数据 7 ab bc cd AB BC CD DA */
题目3:http://poj.org/problem?id=1386
通过很多单词判断能否形成欧拉路径,每个单词只取第一个和最后一个字母,字母看作节点,单词作为有向边,在头部是出度,在尾部是入度,acm可以表示为a→m,先用无向图的方式通过并查集判断是否连通,再以有向图的方式判断是否存在欧拉路径。

#include<stdio.h> #include<iostream> #include<algorithm> #include<cstring> #include<math.h> #include<string> #include<vector> #define ll long long #define inf 0x3f3f3f3f using namespace std; int t,n; char s[1005]; int in[26]; int out[26]; int par[26]; void init() { for(int i=0;i<=25;i++) par[i]=i; } int find(int x) { if(x==par[x]) return x; else return par[x]=find(par[x]); } void unite(int x,int y) { int xx=find(x); int yy=find(y); par[xx]=yy; } int main()///POJ1386 { scanf("%d",&t); while(t--) { init(); memset(in,0,sizeof(in)); memset(out,0,sizeof(out)); scanf("%d",&n); bool flag=true; int x,y; for(int i=1;i<=n;i++) { scanf("%s",s); x=s[0]-'a'; y=s[strlen(s)-1]-'a'; out[x]++; in[y]++; unite(x,y);///先当作无向图连通 } int boss=find(x); for(int i=0;i<=25;i++) { if( (in[i]||out[i]) && find(i)!=boss ) { flag=false; break; } } int st=-1,se=-1; int cnt1=0,cnt2=0;///起点和终点数量 for(int i=0;i<=25;i++) { if(in[i]||out[i]) { int cha=in[i]-out[i]; if(cha==1&&!cnt1)///入度比出度大1,则是终点 se=i,cnt1++; else if(cha==-1&&!cnt2)///出度比入度大1,则是起点 st=i,cnt2++; else if(cha==0) ; else { flag=false; break; } } } if(flag) printf("Ordering is possible. "); else printf("The door cannot be opened. "); } return 0; }
题目4:http://poj.org/problem?id=2513
题意:有25W根木棒,两头各有颜色,用单词表示,相同颜色的头可以连接,问这些木棒能不能连成一条。
思路:把颜色通过字典树转化成数字当作节点,每输入两个就合并。详看代码注释。

#include<stdio.h> #include<iostream> #include<algorithm> #include<cstring> #include<math.h> #include<string> #include<map> #include<queue> #include<stack> #include<set> #include<ctime> #define ll long long #define inf 0x3f3f3f3f const double pi=3.1415926; using namespace std; class node { int id;///第几个颜色,这个将 node* next[30]; node() ///类似java里的构造函数,创建的时候执行清0。不写也没关系,全局变量定义都是默认0 { id=0; memset(next,0,sizeof(next)); } }; node* root=new node;///根节点始终为空 char s1[15],s2[15]; int num[500005];///累计颜色的数量,即度数 int par[500005]; int cnt=0;///标记当前颜色是第几个颜色 void init() { for(int i=0;i<500005;i++) par[i]=i,num[i]=0; ///root=NULL;///自己踩的小坑,加上这一句会Runtime Error,在insert里即NULL->next[x],显然不行 cnt=0; } int find(int x) { if(x==par[x]) return x; else return par[x]=find(par[x]); } void unite(int x,int y) { int xx=find(x); int yy=find(y); par[xx]=yy; } int insert(char* s) { node* p=root; int len=strlen(s); for(int i=0;i<len;i++) { int x=s[i]-'a'; if((p->next[x])==NULL)///当前遍历到的字母还没有开创节点 { p->next[x]=new node();///新开一个节点 p=p->next[x]; } else { p=p->next[x];///不空则进入 } } if(p->id==0)///第一次遇到有颜色在这里结尾,则cnt为这个颜色编号,在num数组里+1 p->id=++cnt; num[p->id]++; return p->id;///返回颜色编号 } int main()///POJ2513 字典树+欧拉路径 { init(); while(scanf("%s %s",s1,s2)!=EOF) { int x=insert(s1); int y=insert(s2); unite(x,y); } int boss=find(1); int flag=true; int deg=0;///统计度数为奇数的点 的个数 for(int i=1;i<=cnt;i++) { if(find(i)!=boss || deg>2)///不连通 或者 奇数度数的点>2 都不可能形成无向图的欧拉路径 { flag=false; break; } if(num[i]%2) deg++; } if(deg!=0 && deg!=2) flag=false; if(flag) printf("Possible "); else printf("Impossible "); }
