目录
20182312 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
1.稀疏图和稠密图,如果e(边数)<n(顶点数)与顶点数取二的对数的乘积,那么称为稀疏图,反之称为稠密图。
2.网:边上带权的图称为网。
3.权:边上带有的和边相关的数据信息。
4.入度出度:无向图中一个点的度为和该点相关联的边的数目。有向图中入度:以该点为终点的边的条数。有向图中出度:以该点为起点的边的条数。有向图中的度为与入度与出度的总和。
5.第一个顶点和最后一个顶点相同且边不重复的路径称为环。
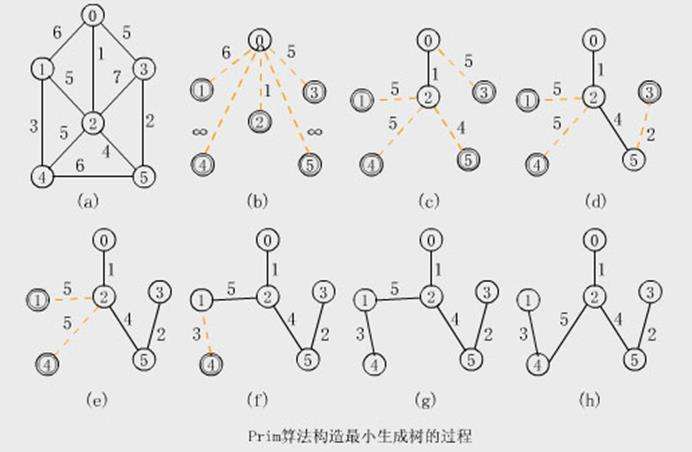
6.最小生成树prim(点)
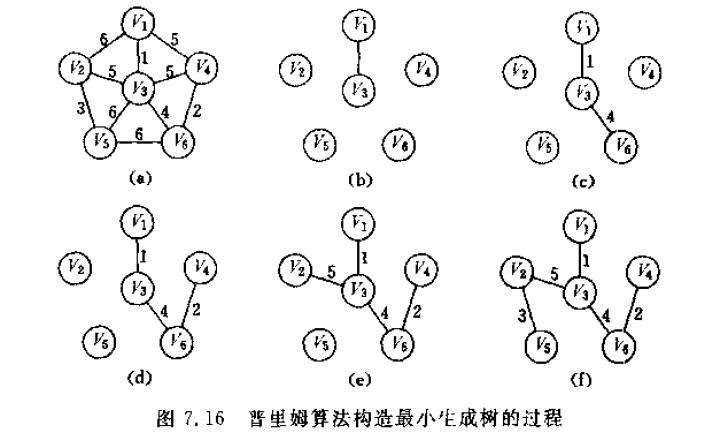
Kruscal(边)
教材学习中的问题和解决过程
- 问题1:怎么判断图是否连通。
- 问题1解决方案:当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所含的顶点数时,图是连通的。
- 问题2:图的深度优先遍历与广度优先遍历在代码中的差异体现在哪里
- 问题2解决方案:广度优先遍历适合使用队列,而深度优先遍历适合使用栈。
代码调试中的问题和解决过程
- 问题1:在用邻接矩阵实现BFS的时候,如果图是不连通的怎么办。
- 问题1解决方案:如下判断队列是否为空,不为空重新调用该方法。
if(!list.isEmpty()){
BFS();
}
- 问题2:在使用邻接表的时候,怎么实现有向图算入度。
- 问题2解决方案:再建个逆邻接表,镜像操作。
代码托管

点评过的同学博客和代码
其他(感悟、思考等,可选)
这一章的概念理解起来不是很难,图的实现也可以从树的那一章寻找到类似的规律,总体来说都算简单。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 130/130 | 2/2 | 23/23 | |
| 第二周 | 451/581 | 3/5 | 42/67 | |
| 第三周 | 451/581 | 3/5 | 42/67 | |
| 第四周 | 617/1068 | 2/7 | 28/95 | |
| 第五周 | 632/1700 | 2/9 | 17/112 | |
| 第六周 | 666/2366 | 1/10 | 22/134 | |
| 第七周 | 1666/4032 | 3/13 | 42/178 | |
| 第八周 | 247/4279 | 1/14 | 3/181 | |
| 第九周 | 2817/7096 | 3/17 | 40/221 | |
| 第十周 | 1002/8098 | 2/19 | 20/241 |
-
计划学习时间:30小时
-
实际学习时间:20小时
-
改进情况:尝试用全局的思维去编代码。