和CPU模式中的内存-cache-寄存器模式一样,GPU也是通过设置全局存储器,局部存储器,寄存器的方式来加速,很多时候我们需要自定义处理数据布局才能真正提高在GPU上的运算速度。
首先,从是否可编程角度,GPU可分为:
1)可编程的存储:寄存器,共享存储,局部存储,常量存储,纹理存储,全局存储;
2)不可编程的存储:L1 cache,L2 cache,常量缓存(只读禁写),只读缓存(纹理,只读禁写)。
从是板载存储(on-board,off-chip)还是片上存储(on-chip)角度,GPU可分为:
1)板载存储:全局存储,局部存储(计算能力2.0之前),常量存储(最大支持64KB),纹理存储;
2)片上存储:寄存器,共享存储,局部存储(CC为3.x时,存储在L1 和L2中,CC在5.x和6.x时,总是在L2上),L1 cache,L2 cache,常量缓存(只读禁写),只读缓存(纹理,只读禁写) 。
从生命周期,GPU可分为:
1)线程:寄存器,局部存储;
2)块:共享存储(核函数内声明表示该变量可被该核函数访问;核函数外声明表示该变量可被所有核函数访问,但是也是块级别的);
3)网格:全局存储,常量存储,纹理存储。
从物理角度,GPU可分为:
1)SM内存储器:
ps:tex 为texture filtering units
i)CC为3.x时:
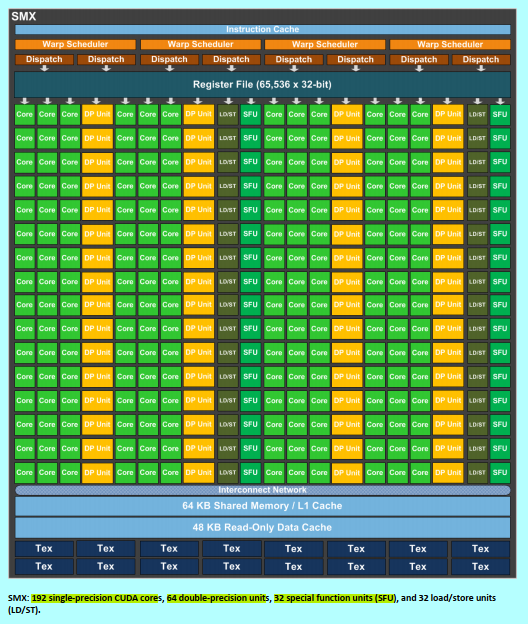
寄存器,64KB(共享存储+L1 cache),只读缓存(纹理,只读禁写,48KB,图1中Read Only),常量缓存(只读禁写,8KB,图1中Constant)??;
ii)CC为5.x时:

寄存器,64KB(共享存储,CC为5.2时是96KB), 24KB(L1+纹理缓存),只读常量缓存(8KB);
iii)CC为6.x时:

寄存器,64KB(共享存储,CC为6.0和6.2时是64KB,为6.1时是96KB),24KB(L1+纹理缓存,CC为6.0和6.2时是24KB,为6.1时是48KB),只读常量缓存(8KB);
iv) CC为7.x时:
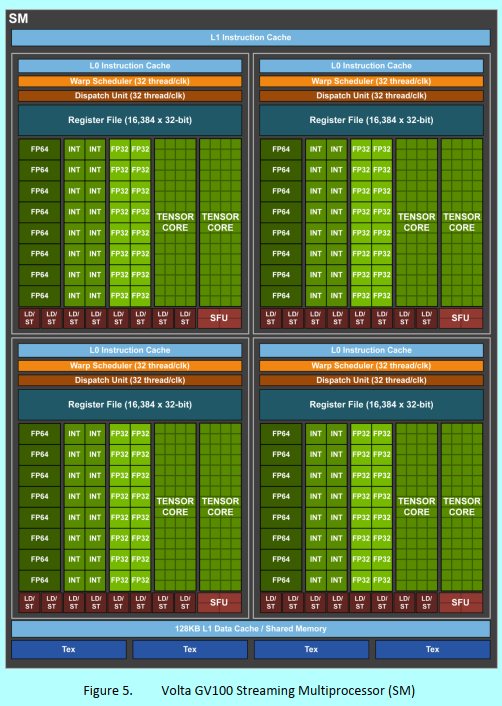
寄存器,128KB(共享存储+数据缓存(即L1+纹理缓存),Volta架构时128KB,Turing时96KB),只读常量缓存(8KB)。
2)SM到全局之间的存储器:L2 cache;
3)板载存储器:全局存储,常量存储(最大支持64KB),纹理存储三者共同所有。
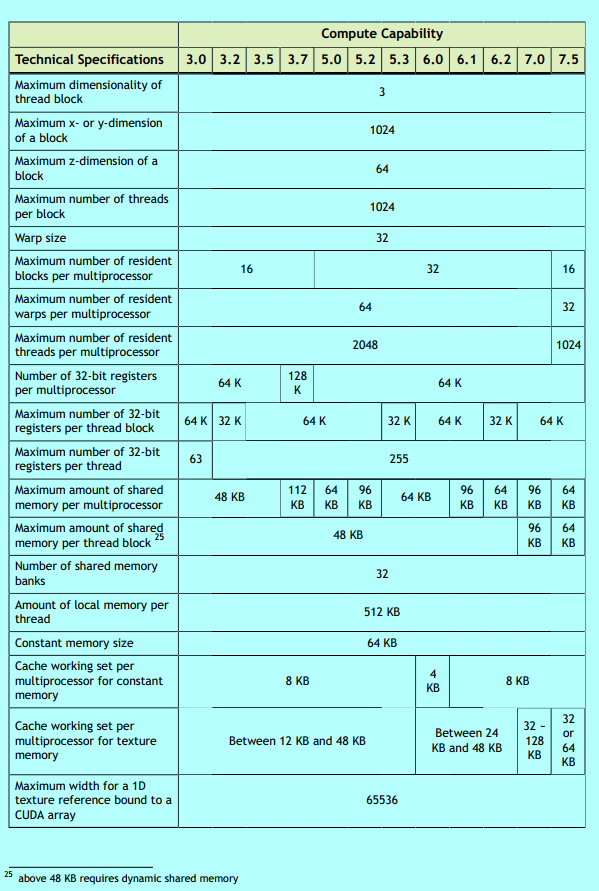
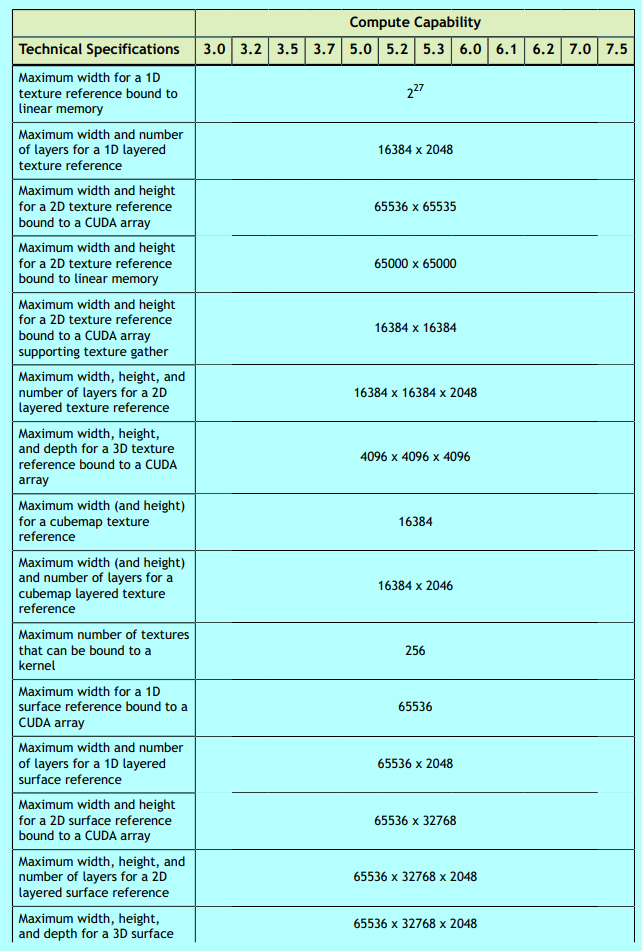

一、存储器访问效率的重要性
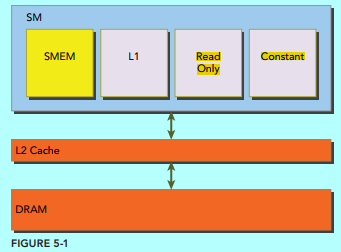
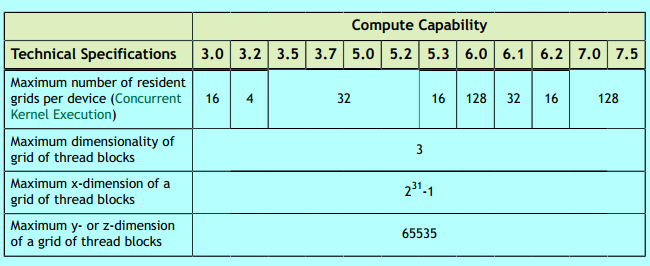
nvidia的显卡中的排布是如图:
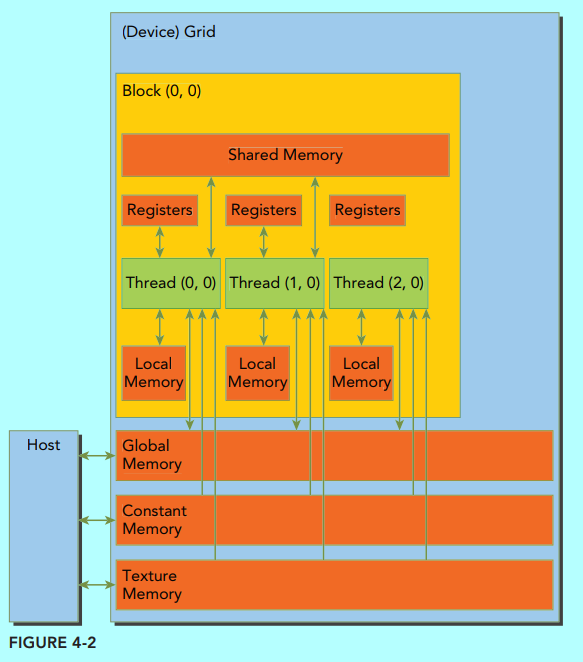

图1.来自《professional cuda c programming》 图2.来自《cuda大规模并行处理器编程实战》
通常CPU和GPU的主存都采用的DRAM(动态随机存取存储器),而低延时内存(如CPU的一级缓存等)用的是SRAM(静态随机存取存储器)。全局存储器是动态随机访问,所以会出现长延时和访问带宽有限的情况,如果很多线程在执行,那么发生拥塞的时候也不影响整个GPU的效率,但是如果拥塞了,而执行的线程很少,都在等着从全局存储器中接收数据,那么结果可想而知,很多的SM就没事可干就得休息了。
这里举个例子:
__global__ void MatrixMulKernel(float *Md,float *Pd,int Width){
int Row = blockIdx.y*TILE_WIDTH+threadIdx.y;//计算矩阵的第几行
int Col = blockIdx.x*TILE_WIDTH+threadIdx.x;//计算矩阵的第几列
float Pvalue= 0;//临时变量
for(int k = 0;k<Witdh;++k){
Pvalue += Md[Row*Width+k]*Nd[k*Witdh +Col];//循环计算行向量乘以列向量
Pd[Row*Width +Col] = Pvalue;//将值赋值给结果矩阵
}
}
上面的代码看出时间主要消耗在for循环中的一次浮点乘和一次浮点加法上,而它们需要访问全局存储器2次,刚好比例是1:1,这个比值被称为CGMA(compute to global memory access),是在某一区域中每次访问全局存储器时执行浮点运算的次数。所以应该提高这个比值,而且通过比较发现GPU的性能主要就在数据传输上,因为SM的计算数据吞吐率远远高于从全局存储器中传输的数据吞吐率,让访问了一次全局存储器之后能够执行不止一次的运算,而不在数据的传输上浪费时间。所以就需要用各种方法来使得数据与流处理器之间的供求关系(现在是供远小于求)能够平衡些。
二、存储设备类型与变量声明类型
跨越不同块的存储器就是全局存储器和常量存储器,这可以通过API让主机对这两种存储器进行读写,不过对于GPU,常量存储器只支持读不支持写,使得能够为GPU提供短延时、高带宽的只读访问。而其他的共享存储、寄存器都是块内的存储器,所以可以不同块之间不相互干涉,达到并行的目的。
寄存器:分配给单一线程,每个线程也只能访问分配给自己的寄存器,可以用来保存那些线程需要频繁访问的变量;在Fermi GPU中,每个线程限制最多63个寄存器,而Kepler GPU每个线程可以有最多255个寄存器。
局部存储:如果一个核函数使用超过硬件限制的寄存器,则会用局部存储来代替多占用的寄存器,通常有:1)编译时使用未知索引引用的局部数组;2)可能会占用大量寄存器空间的较大本地结构体和数组;3)任何不满足核函数集存储限定条件的变量。最开始这块局部存储是直接存储在全局存储器上所以也是高延迟低带宽,对于计算能力2.0及以上的GPU,局部内存数据也存储在每个SM的L1 cache和每个GPU的L2 cache中。
共享存储器:分配给线程块,同一个块中的所有线程都能够访问共享存储器中的变量,所以可以采用线程协作的方式,比如共享块内线程的输入数据和中间的计算结果。共享内存与L1 cache共用64KB的片上内存,通过静态划分形式使用。
常量内存:通过__constant__进行修饰,为板载内存,但是每个SM都有专用的常量缓存器,其必须在全局空间内和所有核函数之外进行声明,对所有计算能力的设备,都只有64KB的常量内存(即一个CUDA程序只有64KB,The 64 KB constant limit is per CUmodule which is a CUDA compilation unit. The concept of CUmodule is hidden under the CUDA runtime but accessible by the CUDA Driver API[7].),其是静态声明的,并对同一编译单元中所有核函数可见。
我们在声明CUDA变量的时候就可以进行不同存储的选择,通过对指定变量的可见性和访问速度来提高整个GPU的计算效率。
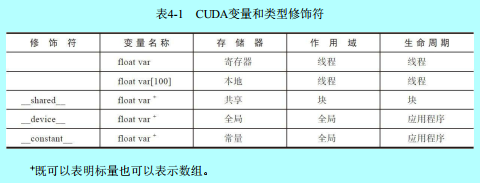
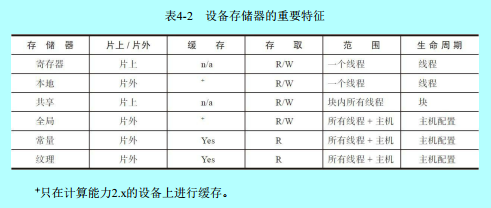
上图就是一个不同的变量类型限定符所影响的变量的作用域和生命周期了,如果作用域是单个线程,那么该变量的会创建很多副本,让每个线程人手一个,从而每个线程只能访问其私有版本的变量;如果想要让变量的生命周期贯穿整个应用程序,记得要放在所有函数体外声明。上表中的除数组外的自动变量是在kernel函数和所有的设备函数中声明的自动标量变量,不过不包含标量变量的数组,例如上面代码中的tx、ty、Pvalue等都是属于这一类。
自动数组变量不存储在寄存器中(不过当所有的访问操作都是通过常数值索引的,那么编译器也可以将自动数组变量存储在寄存器中,也就是编译阶段就知道数组的大小而且知道每个线程需要数组的哪个位置的值),而是存储在全局存储器中,虽然放在全局存储器中,但是作用域却和自动标量变量的作用域相同,也就是每个线程都有一个自动数组变量的私有版本,不过kernel和设备函数中很少需要使用这样的类型,否则也会造成访问延时和潜在的访问拥塞。
a、如果在变量声明前有关键字 __shared__(或者是__device__ __shared__),则它在CUDA中声明一个共享变量(“extern_shared_SharedArray[]”在运行时决定允许使用共享存储器数组的大小)。这样的声明通常在kernel或者设备函数中,其作用域是一个块,也就是一个块中所有的线程看到的是同一个变量,块中的线程都能进行读写,在kernel函数运行的时候,每个块有一个私有版本,生命周期和kernel函数执行周期一致。该变量通常是放在共享存储器上,用来保存全局存储器中kernel函数的执行阶段中需要频繁使用的那部分数据,所以可能需要调整用于创建执行阶段的算法,以便主要集中在全局存储器的小部分数据上。
b、如果在变量声明前有关键字 __constant__(或者是__device__ __shared__),则声明的是常数变量,该变量必须位于任何函数之外。作用域是整个网格,生命周期是整个应用程序的执行过程。一般该变量常用于为kernel函数提供输入值的变量。常数变量存放在全局存储器中(个人:这里的意思应该是说数据是放在全局存储器上但是之前的常数存储器是相对于全局存储器一个缓冲区,可以并行访问),不过采用缓存提高访问效率,访问常数存储器的速度相当快,而且可以并行访问。本书中的时期的时候常数变量的总大小被限制为65535个字节(现在应该不止了),所以可能需要分解输入数据量。
c、如果在变量声明前有关键字 __device__ ,那么该变量是一个全局变量而且放在全局存储器上。可以用来作为块间的线程协作的方法,不过不同块中的线程还没法同步,所以访问全局存储器的时候,线程上也没法保持数据的一致性,除非终止当前执行的kernel。不过该变量通常用来作为一个kernel函数和另一个kernel函数的传递信息。
这里需要注意的是使用在设备存储器上声明的变量的指针的时候有些限制。通常来说,指针是指向全局存储器中的数据对象的。a、如果是主机端函数分配的数据对象,那么通过cudaMalloc()函数初始化得到全局存储器上的内存地址然后作为参数传递给kernel函数(这其中的数据可以通过cudaMemcpy传递过去);b、将全局存储器中变量的地址赋给指针变量,例如{float *ptr = &GlobalVar},将变量GlobalVar的地址赋给自动指针变量ptr。
三、减少全局存储器流量的方法
可以看出全局存储器大,但是访问慢,局部的那些存储器小,可是访问块,所以现在问题就来了,如何将数据划分成不同的小块以存放在局部存储器中,一个重要的划分标准就是块上的kernel函数可以独立的计算每个块,但是注意在给定任意一个kernel函数,不是所有的数据结构都能够划分成块的。
举例:
上图是一个4×4的矩阵与4×4的矩阵相乘的过程,其中将使用2×2的块,也就是Pd矩阵分成四个块来执行,上图显示的是(0,0)块的执行结果,按照矩阵乘法的过程可以看出,得到Pd_(0,0)和Pd_(1,0)两个结果是由两个线程完成的,但是它两都需要访问Md矩阵的第一行的四个值,这就说明Md矩阵的第一行需要被访问两次(这里的前提是分块的第一个块中,当然不同块之间还是会有重复访问的问题);同样的也会访问Nd矩阵的每一行两次,如果说能够采用某种方法使得线程(0,0)和线程(1,0)之间能够合作,那么Md中的元素只要从全局存储器中加载一次就行了,这样对于全局存储器的访问就减少了一半。这里可以发现矩阵乘法这个例子中全局存储器流量潜在的减少量与使用的块的维度成正比,对于N×N的块来说,全局存储器流量就可以减少N倍,也就是流量只有原来的1/N了。
这就是使用线程合作的方式将Md和Nd中的元素加载到共享存储器中,但是共享存储器容量相当小,所以还是得注意,不过可以将矩阵Md和Nd中的元素划分成更小的块,而且块的大小是可以选择的,从而放在共享存储器中。最简单的就是将块的维度等于Md和Nd中分成的块的维度:
通过将Md和Nd两个矩阵也分成2×2的块,然后单独的将不同的块加载到共享存储器中,所以得到的Pd值也被分成几个不同的阶段(这里是分成两个阶段,就是先计算Md_(0,0),Md(1,0)和Nd_(0,0)和Nd(0,1),然后第二个阶段在计算后面一半)。在每个阶段中,一个块中所有的线程相互合作将Md和Nd中的块加载到共享存储器中:
上图就是具体的执行过程,时间从左往右,其中Mds和Nds表示在共享存储器中对应的位置,线程T_(0,0)负责在第一阶段中将Md_(0,0)和Nd_(0,0)加载到对应的共享寄存器中,以此类推,在阶段一中当加载了Md和Nd矩阵的对应的第(0,0)块的时候,计算一半的值;然后进行第二阶段加载Md和Nd矩阵的(0,1)的块然后接着计算后一半的值。
一般来说,如果一个输入矩阵的维度是N而且块大小为TILE_WIDTH(就是想要将这个矩阵分成的小块的维度,比如上面4×4的矩阵分成的小块的维度是2),那么点积运算分成N/TILE_WIDTH个阶段。这种将每个阶段中使用输入矩阵元素的一个很小的子集,这种集中访问的行为称为局部性。所以如果一个算法能够具有这种局部性,那么无论是在多核CPU还是GPU中,都可以提高性能。
下面就是实现上面步骤的例子代码:
代码解释:第一行和第二行进行声明Mds和Nds为共享存储器变量;第三行和第四行将线程索引和块索引放入自动变量中,所以可以利用寄存器来快速的访问这些变量(在函数中自动的标量变量是会放入寄存器中的,作用域是单个线程,也就是每个线程会有tx,ty,bx,by的私有版本);第五行和第六行创建对应的Pd矩阵的行索引和列索引:
上图就是用来解释第五行和第六行的代码的,如何来进行索引Pd矩阵;第八行中m指明点积执行过程中现在执行第几个阶段,每个阶段用到Md中的一个块元素和Nd中的一个块元素,表示已经执行完Md和Nd中m×TILE_WINDTH对元素了;
第九行和第十行就是通过一个块中的线程协作的方式将Md和Nd中一个块内的数据加载到共享存储器中,因为这里还是将2维矩阵以1维向量存储的方式,所以先跳过前面的Row*Width个,从第(Row+1)行开始计算;第十一行使用栅栏同步函数_syncthreads(),确保同一个块中所有的线程都加载好了Mds和Nds;第十二行和第十三行用来计算第m个阶段上的点积部分;第十四行再次调用栅栏同步函数,用于进入下一次的循环中加载Md和Nd的下一个块,保证当前块中所有的线程都已经使用完Mds和Nds的数据。
虽然采用寄存器,共享存储器和常数存储器可以有效的减少对全局存储器的访问,但是它们自身也是有容量限制的,如果说每个线程要求的存储单元越多,那么每个SM中可以同时驻留的线程就越少,导致在整个存储器中驻留的线程数也越少。假设(G80中)一个SM中寄存器大小为8KB,而且最多能够容纳768个线程,那么每个线程可使用的寄存器个数为8KB/768 = 10.如果每个线程使用11个寄存器,那么线程数目势必要减少,而且是以块的形式来减少的,如果当前块中执行的有256个线程,那么算下来每个SM中可同时驻留的线程数就减少256个,只有512个,使得大大减少线程调度是可用的warp的数量(个人:这里的SM中可以最大驻留768个线程,而一个SM中的寄存器是放在一起的不是单独线程分开的,然后你在kernel函数中指定了块的维度,也就是一个块中有256个线程,那么方便调度就从768减去256,如果寄存器还是不够用那么接着在减少256个线程,这样就使得在kernel中分配的块能够放在一个SM中运行);同样的共享存储器也是个问题,假设(G80)每个SM中共享存储器的大小为16KB,而这总的16Kb是以块划分而不是像上面的8KB的寄存器一样以线程划分,如果每个块使用5KB的共享存储器,那么每个SM最多只能分配3个块。在上面的代码例子中,假设对于16×16的块来说,每个块使用16×16×4 = 1KB的存储空间来存放Mds,同理需要1KB空间存放Nds,每个块需要使用2KB的共享存储空间,但是因为线程的硬件限制,每个SM最多容纳768个线程,使得最多只有3个块,那么只能使用共享存储器的6KB的空间,就浪费了10KB的空间了,不过硬件的限制是因显卡的更新换代而不同的,比如GT200中每个SM最大支持1024个线程。
总结:这里的块有涉及到kernel函数的人为分配,也有SM的硬件支持上限,寄存器的容量,共享存储器的容量还有全局存储器的访问流量 都会制约程序的运行性能,值得一提的是,这种思想也可以用在多核CPU上,数据的局部性可以使得利用CPU自带的寄存器来减少访问内存的次数,也能够加快程序的运行。
附加:关于常量存储器和纹理存储器
常量存储器
按照之前说的常量存储器虽然小,而且设备代码无法改变其中的数据,但是却能够提供快速的并行全局访问机制。在《GPU高性能编程CUDA实战》中说NVIDIA硬件提供了64KB的常量存储,这个是书本说的,有可能现在的显卡提供更大的存储,或者还是64KB,不过这里按照64KB来说明原理。
通过在变量前面添加关键字__constant__ 例如:__constant__ int a;或者__constant__ int s[10],这时候不是通过cudaMalloc()来为指针分配GPU内存,而且无需使用cudaFree()来释放指针,只需要为这个指针指向的内存提交一个固定大小就行。而且这里通过这个关键字声明的变量可以放在任何函数的外部,因为常量存储是全局的存储器,所以无需和共享存储器一样放在kernel等函数内部。不过这里可以通过采用不同于cudaMemcpy()的复制函数将主机的数据与GPU的常量存储器之间进行数据的交换:
cudaMemcpyToSymbol(dev_mem,host_mem,sizeof(/*yourdata*/));
在《大规模并行处理器编程实战》中第八章可以通过使用cudaMemcpy来将主机的数据复制到常量存储器中,而《GPU高性能编程CUDA实战》中却是说“cudaMemcpyToSymbol()与参数为cudaMemcpyHostToDevice()的cudaMemcpy()之间唯一差异在于前者会复制到常量存储器,而后者会复制到全局存储器”,这里有可能是其中一本书有误,或者是不同时期的处理方式不同,不过都可以试试。(留待测试)
常量存储器带来的好处在于:
A、 对常量存储的单次读操作可以广播到其他临近的线程,并且节约15次读取的操作。这是与warp相关的,在前面说过warp是指在sm中调度的单位,其中包含了32个线程,会在线程块中被划分成不同的warp然后被使用,而在处理常量存储的时候,硬件会将单次存储器的读取操作广播到每个半warp,也就是16个线程,如果在半warp中每个线程都从常量存储器的相同地址上读取数据,那么只会产生一次读取请求然后将数据广播到这16个线程中。
B、 常量存储器的数据会被缓存起来,对于相同地址的连续读操作将不再会产生额外的内存通信,这个也是上面a带来的好处。
但是这个的坏处在于如果半warp中每个线程访问的不是同一个地址的数据,那么就没法享受到这种好处了,这时候这16次不同的读取操作会被串行化,从而需要16倍的时间来发出请求,但是如果从普通的全局存储器中读取,那么这些请求会同时发出,所以这样算来,常量存储器还慢于全局存储器中的数据读取。
纹理存储器
相比较于常量存储器,纹理存储器是另一种类型的只读存储器,在特定的访问模式中,纹理存储器也能够提升性能并减少存储器上的通信流量,虽然它最初是针对传统的图形处理应用程序而设计的,NVIDIA为OpenGL和DirectX等的渲染流水线都设计了纹理单元,但是在一些GPU计算应用程序中同样非常有用;与常量存储器类似的是,纹理存储器同样缓存在芯片上,所以在一定情况下它能够减少对内存的请求并提供更高效的内存带宽,纹理缓存是专门为单存储器访问模式中存在大量空间局部性的图形应用程序而设计的,而在某个计算应用程序中,这就意味这一个线程读取的位置可能与邻近线程读取的位置“非常接近“:
从数学角度来看,上图的四个地址不是连续的,在一般的CPU缓存模式中,这些地址将不会缓存,但是因为GPU纹理缓存是专门为了加速这种访问模式而设计的,所以如果在这种情况下使用纹理存储器而不是全局存储器,那么性能可以被提升,而且这种访问在通用计算中也不是那么罕见的。(这段文字纯照搬书上的)。
1、使用一维纹理内存
首先,需要将输入的数据声明为texture类型的引用,这里举例将浮点类型进行声明为纹理类型的变量:
//这些变量将位于GPU上 texture<float> texConstSrc; texture<float> texIn; texture<float> texOut;
接下来就是需要将在为三个缓冲区分配GPU内存之后,需要通过cudaBindTexture()函数将这些变量绑定到对应的内存缓冲区上,使得:将指定的缓冲区作为纹理来使用;将纹理引用作为这些纹理的“名字”。(个人:看得出来这并不是一种额外的硬件实现的存储器,而是在全局存储器上申请内存然后采用绑定的方法实现的)
cudaMalloc( (void**)&dev_inSrc,imageSize ) ; cudaMalloc( (void**)&dev_outSrc,imageSize ) ; cudaMalloc( (void**)&dev_constSrc,imageSize ) ; cudaBindTexture( NULL, texConstSrc,dev_constSrc,imageSize ) ; cudaBindTexture( NULL, texIn,dev_inSrc,imageSize ) ; cudaBindTexture( NULL, texOut,dev_outSrc,imageSize ) ;
如上面代码所示,先使用cudaMalloc进行申请内存,然后采用函数cudaBindTexture()函数进行纹理变量与申请的内存进行绑定。
在启动核函数之后,需要读取纹理内存时,是采用特殊的函数来读取的,,采用tex1Dfetch()函数,这是一个编译器内置函数,而且纹理引用必须声明为文件作用域内的全局变量,该函数的原型为:
template<class T> T tex1Dfetch(cudaTextureObject_t texObj, int x);
该函数提取的是由一维纹理对象texObj和整数纹理坐标x指定的线性内存中的区域。 tex1Dfetch()只适用于非规范化的坐标,所以只支持边界和钳位寻址模式。它不执行任何纹理过滤。对于整数类型来说,它可以选择性的将该整数提升到单精度浮点数。(该函数在CUDA_C_Programming_Guide.pdf中,其中也有许多其他的纹理函数,不过因为在GPU高性能编程CUDA实战第七章中暂时只涉及这个函数而已,其他的函数留待后续扩充)。
这里举个例子:
__global__ void blend_kernel( float *dst,bool dstOut ) {
// map from threadIdx/BlockIdx to pixel position
int x = threadIdx.x + blockIdx.x * blockDim.x;//需要理解
int y = threadIdx.y + blockIdx.y * blockDim.y;//需要理解
int offset = x + y * blockDim.x * gridDim.x;//需要理解
int left = offset - 1;
int right = offset + 1;
if (x == 0) left++;
if (x == DIM-1) right--;
int top = offset - DIM;
int bottom = offset + DIM;
if (y == 0) top += DIM;
if (y == DIM-1) bottom -= DIM;
float t, l, c, r, b;//top,left,center,right,bottom
if (dstOut) {
t = tex1Dfetch(texIn,top);
l = tex1Dfetch(texIn,left);
c = tex1Dfetch(texIn,offset);
r = tex1Dfetch(texIn,right);
b = tex1Dfetch(texIn,bottom);
} else {
t = tex1Dfetch(texOut,top);
l = tex1Dfetch(texOut,left);
c = tex1Dfetch(texOut,offset);
r = tex1Dfetch(texOut,right);
b = tex1Dfetch(texOut,bottom);
}
dst[offset] = c + SPEED * (t + b + r + l - 4 * c);//采用一维数组并计算偏移来实现一个算法
}
上面的代码表示的意思这里无需理解,只知道是采用的一维数组实现的,而且是计算当前点和这个点四周的四个点。这里使用的是1维数组存储的,所以在计算top,left等的时候需要计算偏移。
在最后先要解绑纹理缓冲区,然后接着进行释放全局缓冲区:
cudaUnbindTexture( texIn ); cudaUnbindTexture( texOut ); cudaUnbindTexture( texConstSrc ); cudaFree( dev_inSrc ); cudaFree( dev_outSrc ); cudaFree( dev_constSrc );
2、使用二维纹理内存
在很多情况下使用二维的线程块和线程格是非常有用的。首先,需要修改之前的纹理引用的声明:
texture<float,2> texConstSrc; texture<float,2> texIn; texture<float,2> texOut;
这里在访问之前的纹理存储器的时候,就无需使用tex1Dfetch()函数了,因为采用了二维纹理内存之后,就可以直接使用x和y来进行访问,而无需计算偏移量来进行访问了,而且当使用tex2D()时,无需担心发生溢出的问题,如果x或y小于0,那么tex2D()将返回0处的值;同理如果某个值大于最大值,那么该函数就返回最大值处的值。
__global__ void blend_kernel( float *dst,
bool dstOut ) {
// map from threadIdx/BlockIdx to pixel position
int x = threadIdx.x + blockIdx.x * blockDim.x;
int y = threadIdx.y + blockIdx.y * blockDim.y;
int offset = x + y * blockDim.x * gridDim.x;
float t, l, c, r, b;
if (dstOut) {
t = tex2D(texIn,x,y-1);
l = tex2D(texIn,x-1,y);
c = tex2D(texIn,x,y);
r = tex2D(texIn,x+1,y);
b = tex2D(texIn,x,y+1);
} else {
t = tex2D(texOut,x,y-1);
l = tex2D(texOut,x-1,y);
c = tex2D(texOut,x,y);
r = tex2D(texOut,x+1,y);
b = tex2D(texOut,x,y+1);
}
dst[offset] = c + SPEED * (t + b + r + l - 4 * c);
}
从上面的代码可以看出,在计算当前点周围的四个点的时候,已经无需先计算偏移量,可以直接使用x和y来计算,不过这里的存储还是使用的1维数组来存储的。
不过与一维纹理相比,这里的绑定部分略有不同:
cudaMalloc( (void**)&dev_inSrc,imageSize ); cudaMalloc( (void**)&dev_outSrc,imageSize ); cudaMalloc( (void**)&dev_constSrc,imageSize );
cudaChannelFormatDesc desc = cudaCreateChannelDesc<float>(); cudaBindTexture2D( NULL, texConstSrc,dev_constSrc,desc, DIM, DIM,sizeof(float) * DIM ); cudaBindTexture2D( NULL, texIn,dev_inSrc,desc, DIM, DIM,sizeof(float) * DIM ); cudaBindTexture2D( NULL, texOut,dev_outSrc,desc, DIM, DIM,sizeof(float) * DIM );
上述代码看得出来,这里多了一个函数,因为在绑定二维纹理的时候,运行时系统要求提供一个cudaChannelFormatDesc。,这里使用的是默认的参数,并且只提供了一个浮点描述符,然后通过cudaBindTexture2D(),纹理的维数(DIM*DIM)以及通道格式描述符(desc),将三个缓冲区绑定为二维纹理。
虽然在绑定的时候使用的是不同的函数,但是在解绑的时候却是一样的吗所以解绑部分的代码可以完全不用修改如一维纹理内存部分一样。
总结:对于纹理存储器部分,了解的还不多,也没怎么用,所以理解的不深刻,留待后续更深刻了再来加深。
参考文献:
1 - 《大规模并行处理器编程实战》第四节
2 - 《programming massively parallel processors a hands-on-approach》,现在有第三版
3 - coursera上有上面书籍作者的讲课视频(是差不多60%其大学的内容),有兴趣的可搜索“Heterogeneous Parallel Programming”。
4 - 《professional cuda c programming》
5 - https://forums.developer.nvidia.com/t/constant-cache/61133
6 - https://forums.developer.nvidia.com/t/sm-share-memory-size-constant-size/56377
7 - https://stackoverflow.com/questions/10256402/why-is-the-constant-memory-size-limited-in-cuda






