判断单链表是否有环，有一个很简单的算法，即快慢指针算法。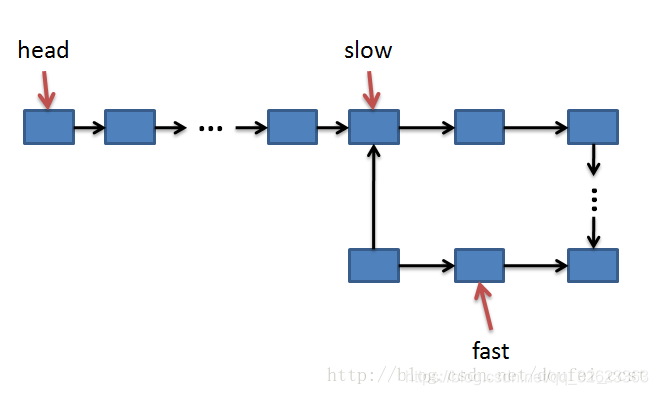

判断单链表是否有环，有一个很简单的算法，即快慢指针算法。

我们可以创建两个指针，一个慢指针slow，一个快指针fast，都是从头结点开始往后遍历。其中满指针一次走一步，即slow = slow->next;，而快指针一次走两步，即fast = fast->next->next;，如果链表有环，那么这两个指针必然会相遇，否则fast指针若先指向了NULL，那么显然链表是可以穷尽的，也就自然就没有环了。

大家如果想练手可以去：https://leetcode-cn.com/problems/linked-list-cycle/
下面放上我的代码：

/** * Definition of singly-linked-list: * class ListNode { * public: * int val; * ListNode *next; * ListNode(int val) { * this->val = val; * this->next = NULL; * } * } */ class Solution { public: /** * @param head: The first node of linked list. * @return: True if it has a cycle, or false */ bool hasCycle(ListNode * head) { // do the null case if(head == NULL) return false; ListNode* fast = head; ListNode* slow = head; // 只需判断fast指针是否为空就行了，毕竟它走得快 while(fast != NULL) { slow = slow->next; // 如果能走到空指针，则一定不是环 if(fast->next == NULL || fast->next->next == NULL) return false; else fast = fast->next->next; // the true case if(slow == fast) return true; } return false; } };

网传的判断是否有环的方法还有穷举法和hash表法，不过都没快慢指针法这么好，大家有兴趣可以自行去了解一下。
好，既然我们已经学会如何判断单链表是否有环了，那又如何找到这个环的入口地址呢？

其实啊，这也不难，只要对上面那个算法进行一些补充就行了。
我们先来细致地分析一下上面的快慢指针。
你们可以在纸上模拟一下，或者稍微想一想，就能发现，当快慢指针相遇的时候，慢指针要么还没走完一遍全程，要么刚好走完全程，而且刚好走完全程的情况是这整个链表都是一个环。

我们直接讨论一般情况。看下图，A为起点，B为环的入口节点，C为快慢指针相遇节点，中间的其余节点均省略没画了。A到B的距离为S，B到C的距离为t，C到B的距离为X。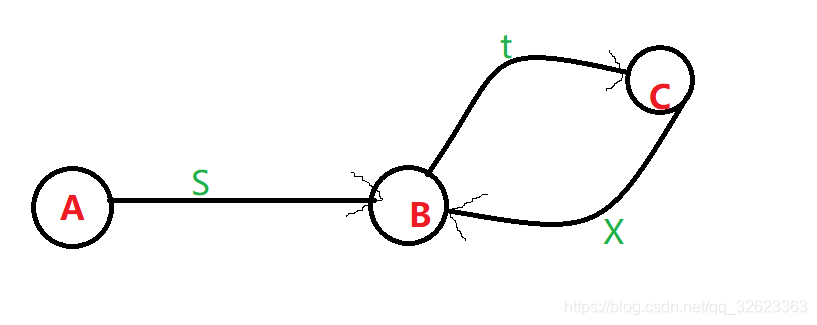

那么，在两个指针相遇的时候，
慢指针共走过的路程为（A->B->C）：s+t
快指针共走过的路程为（A->B->C->B->C）：s+t+x+t
而且因为快指针走过的速度是慢指针两倍，因此：s+t+x+t = 2*(s+t)
因此可以得出，x=s
这意味着，从A到B的距离和从C到B的距离是相同的！
那么，如果我们在快慢指针相遇之后，让慢指针继续走下去，而同时让另一个指针从A节点出发往B走，那么它们俩相遇的那个节点，就一定会是B节点，即这个环的入口节点！

嘿嘿，大家可以试试这道题：https://leetcode-cn.com/problems/linked-list-cycle-ii/
我的代码：

/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode *detectCycle(ListNode *head) { ListNode* slow = head; ListNode* fast = head; while(fast != NULL) { slow = slow->next; if(fast->next == NULL || fast->next->next == NULL) return NULL; else fast = fast->next->next; if(fast == slow) { fast = head; while(fast!=slow) { fast = fast->next; slow = slow->next; } return slow; } } return NULL; } };

---

用上面的方法，我们就可以很轻松地解决另一道题了，即：如何判断两个单链表是否相交，别小看这道题，这道题在有环的情况下就需要是用到上面刚刚学到的算法啦！详解请看：https://blog.csdn.net/qq_32623363/article/details/87885938