- 时间复杂度:O(nlogn)
- 空间复杂度:O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序
- 稳定性:归并排序是稳定的排序算法,
temp[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];这行代码可以保证当左右两部分的值相等的时候,先复制左边的值,这样可以保证值相等的时候两个元素的相对位置不变。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。把长度为n的输入序列分成两个长度为n/2的子序列;对这两个子序列分别采用归并排序;将两个排序好的子序列合并成一个最终的排序序列。
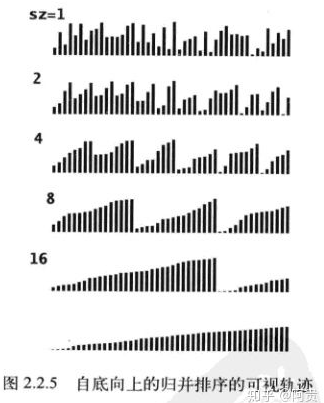
从下图可以看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。

图示过程
(1) 归并排序的流程
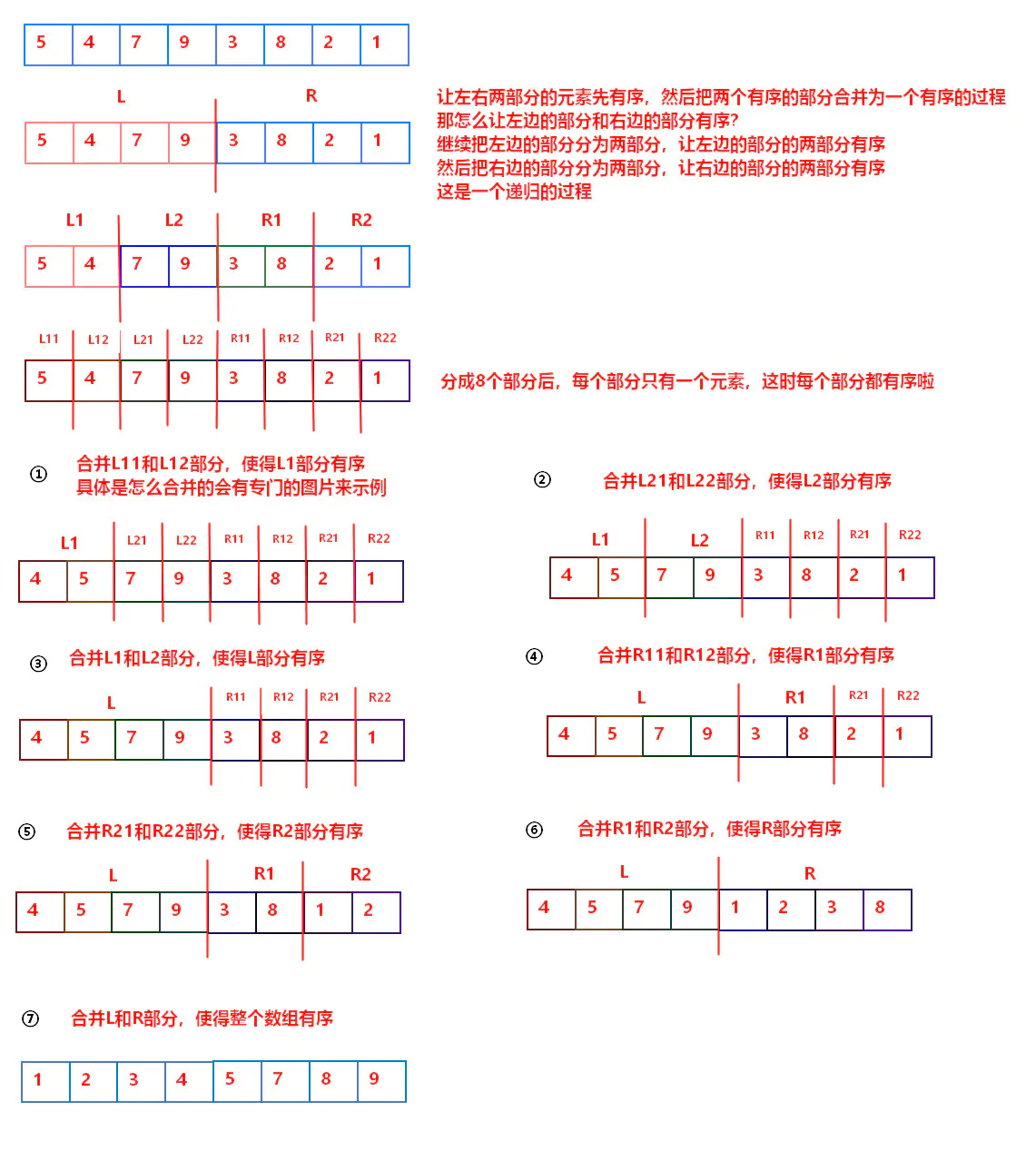
(2) 合并两个有序数组的流程
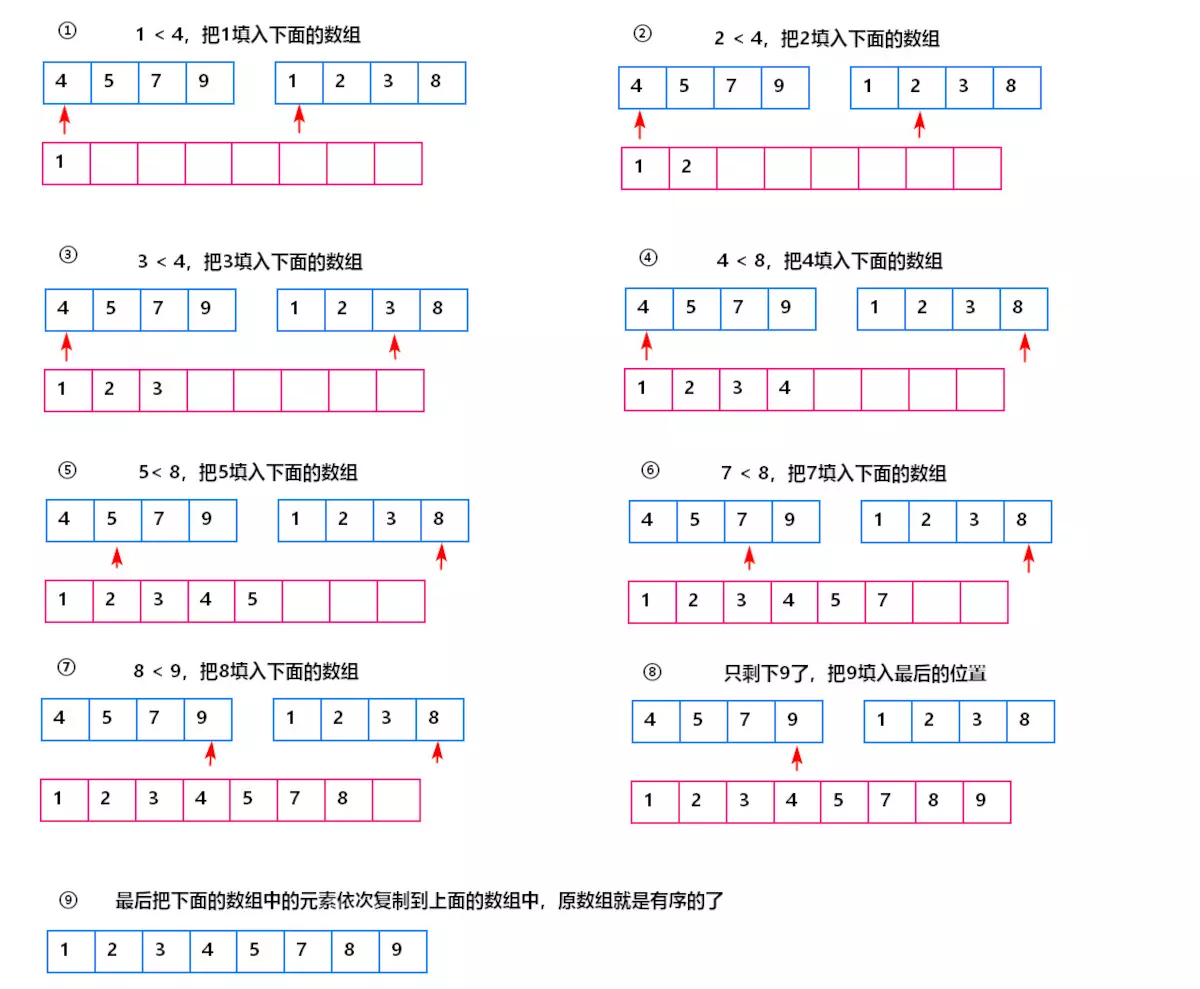
归并排序有两种实现方式: 基于递归的归并排序和基于循环的归并排序。(也叫自顶向下的归并排序和自底向上的归并排序)
这两种归并算法虽然实现方式不同,但还是有共同之处的:
1. 无论是基于递归还是循环的归并排序, 它们调用的核心方法都是相同的:完成一趟合并的算法,即两个已经有序的数组序列合并成一个更大的有序数组序列 (前提是两个原序列都是有序的!)
2. 从排序轨迹上看,合并序列的长度都是从小(一个元素)到大(整个数组)增长的
C++
一、基于递归的归并排序(自顶向下的归并排序)
void MergeSort (int arr [], int low,int high) { if(low>=high) { return; } // 终止递归的条件,子序列长度为1 int mid = low + (high - low)/2; // 取得序列中间的元素 MergeSort(arr,low,mid); // 对左半边递归 MergeSort(arr,mid+1,high); // 对右半边递归 merge(arr,low,mid,high); // 合并 } void merge(int arr[],int low,int mid,int high){ //low为第1有序区的第1个元素,i指向第1个元素, mid为第1有序区的最后1个元素 int i=low, j=mid+1, k=0; //mid+1为第2有序区第1个元素,j指向第1个元素 int *temp=new int[high-low+1]; //temp数组暂存合并的有序序列 while(i<=mid&&j<=high){ if(arr[i]<=arr[j]) //较小的先存入temp中 temp[k++]=arr[i++]; else temp[k++]=arr[j++]; } while(i<=mid)//若比较完之后,第一个有序区仍有剩余,则直接复制到t数组中 temp[k++]=arr[i++]; while(j<=high)//同上 temp[k++]=arr[j++]; for(i=low,k=0;i<=high;i++,k++)//将排好序的存回arr中low到high这区间 arr[i]=temp[k]; delete []temp;//释放内存,由于指向的是数组,必须用delete [] }
基于递归归并排序的优化方法
优化一:对小规模子数组使用插入排序
用不同的方法处理小规模问题能改进大多数递归算法的性能,因为递归会使小规模问题中方法调用太过频繁,所以改进对它们的处理方法就能改进整个算法。因为插入排序非常简单, 因此一般来说在小数组上比归并排序更快。 这种优化能使归并排序的运行时间缩短10%到15%。
怎么切换呢?只要把作为停止递归条件的
if(low>=high) { return; }改成
if(high - low <= 10) { // 数组长度小于10的时候
InsertSort(int arr[], int low,int high) // 切换到插入排序
return;
}就可以了,这样的话,这条语句就具有了两个功能:
1. 在适当时候终止递归
2. 当数组长度小于M的时候(high-low <= M), 不进行归并排序,而进行插排
优化二: 测试待排序序列中左右半边是否已有序
通过测试待排序序列中左右半边是否已经有序, 在有序的情况下避免合并方法的调用。
因为a[low...mid]和a[mid...high]本来就是有序的,存在a[low]<a[low+1]...<a[mid]和a[mid+1]<a[mid+2]...< a[high]这两种关系, 如果判断出a[mid]<=a[mid+1]的话,我们就认为数组已经是有序的并跳过merge() 方法。
void sort (int a[], int low,int high) {
if(low>=high) {
return;
} // 终止递归的条件
int mid = low + (high - low)/2; // 取得序列中间的元素
sort(a,low,mid); // 对左半边递归
sort(a,mid+1,high); // 对右半边递归
if(a[mid]<=a[mid+1]) return; // 避免不必要的归并
merge(a,low,mid,high); // 单趟合并
}优化三:去除原数组序列到辅助数组的拷贝
在上面介绍的基于递归的归并排序的代码中, 我们在每次调用merge方法时候,我们都把arr对应的序列拷贝到辅助数组temp中去。
在递归调用的每个层次交换输入数组和输出数组的角色,从而不断地把输入数组排序到辅助数组,再将数据从辅助数组排序到输入数组,节省数组复制的时间。
注意, 外部的sort方法和内部sort方法接收的a和aux参数刚好是相反的
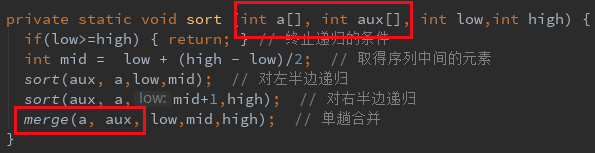
在这里我们做了两个操作:
- 在排序前拷贝一个和原数组元素完全一样的辅助数组(不再是创建一个空数组了!)
- 在递归调用的每个层次交换输入数组和输出数组的角色
因为外部sort和merge的参数顺序是相同的,所以,无论递归过程中辅助数组和原数组的角色如何替换,对最后一次调用的merge而言(将整个数组左右半边合为有序的操作), 最终被排为有序的都是原数组,而不是辅助数组!

void MergeSortCore(int* data, int* copy, int first, int last); void MergeSort(int* data, int length) { if(data == NULL || length <= 0) return; int* copy = new int[length]; for(int i = 0; i < length; i++) copy[i] = data[i]; MergeSortCore(data, copy, 0, length - 1); for(int i = 0; i < length; i++) data[i] = copy[i]; delete[] copy; return; } void MergeSortCore(int* data, int* copy, int first, int last) { if(first == last) copy[first] = data[first]; else { int mid = first + (last - first)/2; MergeSortCore(copy, data, first, mid); MergeSortCore(copy, data, mid + 1, last); //merge int i = first, j = mid + 1; int k = first; while(i <= mid && j <= last) { if(data[i] <= data[j]) copy[k++] = data[i++]; else copy[k++] = data[j++]; } while(i <= mid) copy[k++] = data[i++]; while(j <= last) copy[k++] = data[j++]; } }
注意:优化结果虽然差不多,但是当其数组接近有序的时候,速度有了可观的提升。

二、基于循环的归并排序(自底向上)
void sort(int a []){ int N = a.size(); for (int size = 1; size < N; size *= 2){ // low+size=mid+1,为第二个分区第一个元素,它 < N,确保最后一次合并有2个区间 for(int low = 0; low + size < N;low += 2 * size) { mid = low + size - 1; high = low + 2 * size - 1; if(high > N-1) high = N - 1; merge(a,low, mid, high); } } }