第二章 数学基础
概率论基础
信息论基础: 熵、联合熵、相对熵、困惑度、互信息、噪声信道模型

熵又称为自信息,表示信息X每发出一个符号(不论发什么符号)所提供的平均信息量。熵也可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大,它的不确定性越大。那么, 正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量以确定其值。





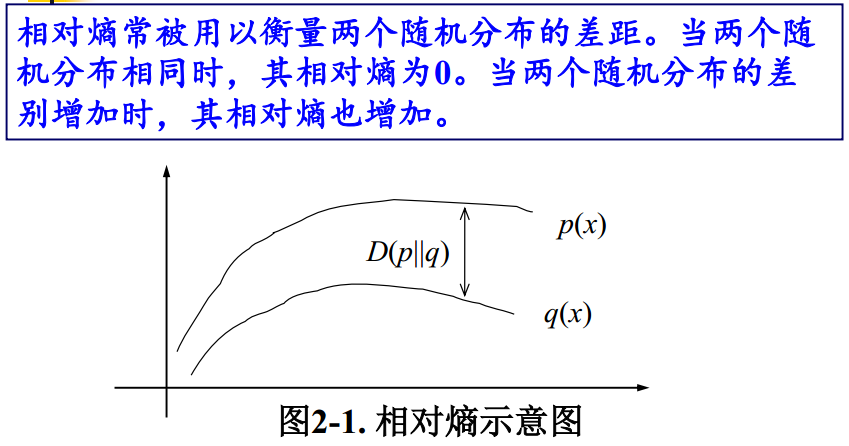
相对熵常被用以衡量两个随机分布的差距。当两个随机分布相同时,其相对熵为0。当两个分布的差别增加时,其相对熵也增加。





互信息 I(X; Y)是在知道了 Y的值以后X的不确定性的减少量,即Y的值透露了多少关于X的信息量。









应用举例: 词义消歧


















词义消歧 是基本问题 : 如何区分不同上下文中的词汇语义。
基本思路:没歌词表达不同的含义时其上下文(语境)往往不同,也就是说,不同的词义对应不同的上下文,因此,如果能够将多义词的上下文区别开,其词义自然就明确了。
基于上下文分类
1. 贝叶斯分类器 argmax p (si | C)
2. 基于最大熵的消歧方法
基本思想:在只掌握关于未知分布的部分知识的情况下, 符合已知知识的概率分布可能有多个,但使熵值最大的概率分布最真实地反映了事件的分布情况,因为熵定义了随机变量的不确定性,当熵最大时,随机变量最不确定。也就是说,在已知部分知识的前提下,关于未知分布最合理的推断应该是符合已知知识最不确定或最大随机的推断。
位置无关:词袋模型;
位置有关:模板表示;
特征的类型:词性 词形 double
