卡特兰数

先给出卡特拉数模板：

const int C_maxn = 1e4 + 10;
LL CatalanNum[C_maxn];
LL inv[C_maxn];
inline void Catalan_Mod(int N, LL mod)
{
    inv[1] = 1;
    for(int i=2; i<=N+1; i++)///线性预处理 1 ~ N 关于 mod 的逆元
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;

    CatalanNum[0] = CatalanNum[1] = 1;

    for(int i=2; i<=N; i++)
        CatalanNum[i] = CatalanNum[i-1] * (4 * i - 2) %mod * inv[i+1] %mod;
}

卡特兰大数模板：

#include<bits/stdc++.h>
using namespace std;
const int C_maxn = 100 + 10;///项数

int Catalan_Num[C_maxn][1000];///保存卡特兰大数、第二维为具体每个数位的值
int NumLen[C_maxn];///每个大数的数长度、输出的时候需倒序输出

void catalan() //求卡特兰数
{
    int i, j, len, carry, temp;
    Catalan_Num[1][0] = NumLen[1] = 1;
    len = 1;
    for(i = 2; i < 100; i++)
    {
        for(j = 0; j < len; j++) //乘法
        Catalan_Num[i][j] = Catalan_Num[i-1][j]*(4*(i-1)+2);
        carry = 0;
        for(j = 0; j < len; j++) //处理相乘结果
        {
            temp = Catalan_Num[i][j] + carry;
            Catalan_Num[i][j] = temp % 10;
            carry = temp / 10;
        }
        while(carry) //进位处理
        {
            Catalan_Num[i][len++] = carry % 10;
            carry /= 10;
        }
        carry = 0;
        for(j = len-1; j >= 0; j--) //除法
        {
            temp = carry*10 + Catalan_Num[i][j];
            Catalan_Num[i][j] = temp/(i+1);
            carry = temp%(i+1);
        }
        while(!Catalan_Num[i][len-1]) //高位零处理
        len --;
        NumLen[i] = len;
    }
}

int main(void)
{
    catalan();
    for(int i=1; i<=30; i++){
        for(int j=NumLen[i]-1; j>=0; j--){
            printf("%d", Catalan_Num[i][j]);
        }puts("");
    }
    return 0;
}

题目链接：http://172.18.66.54:50015/problem.php?id=1470

题目描述

    czz在水果拼盘里挑了一片水果，这个水果是一个凸n边形，他只想吃三角形的，所以他打算把它沿着顶点切成三角形， 有多少种方案呢？czz想考考AW，AW犯了难，请你帮他算算有多少种取法，答案对1e9+7取模。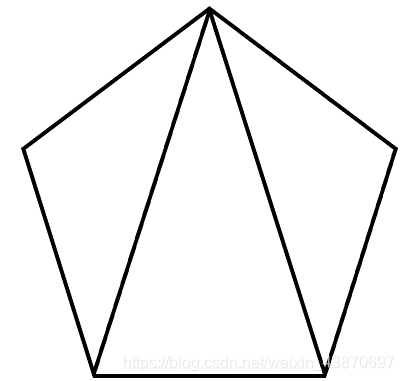

输入

一个整数T (0<T<100)
每组数据一个整数n (2<n<105)

输出

方案数对1e9+7取模

样例输入

2
3
4

样例输出

1
2

凸多边形的三角形划分，求卡特兰数。

选择一个基边，显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1pn，我们就可以用p1、pn和另外一个点假设为pi做一个三角形，并将多边形分成三部分，除了中间的三角形之外，一边是i边形，另一边是n-i+1边形。i的取值范围是2到n-1。所以本题的解c(n)=c(2)*c(n-1)+c(3)*c(n-2)+...c(n-1)*c(2)。令t(i)=c(i+2)。则t(i)=t(0)*t(i-1)+t(1)*t(i-2)...+t(i-1)*t(0)。很明显，这就是一个卡特兰数了。

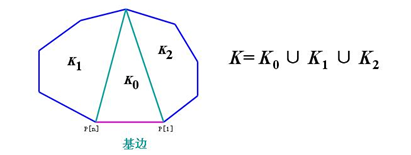
代码：

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
const int C_maxn = 1e5 + 7;
long long CatalanNum[C_maxn];
long long inv[C_maxn];
inline void Catalan_Mod(int N)
{
    inv[1] = 1;
    for (int i = 2; i <= N + 1; i++)///线性预处理 1 ~ N 关于 mod 的逆元
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
 
    CatalanNum[0] = CatalanNum[1] = 1;
 
    for (int i = 2; i <= N; i++)
        CatalanNum[i] = CatalanNum[i - 1] * (4 * i - 2) % mod * inv[i + 1] % mod;
}
int main()
{
    Catalan_Mod(100010);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        cout << CatalanNum[n-2] << endl;
    }
}