此作业的要求参见:https://edu.cnblogs.com/campus/nenu/2020Fall/homework/11245
coding代码的地址:https://e.coding.net/xucancan1/sizeyunsuan/sizeyunsuan.git
程序使用说明:在功能1和功能4文件夹中f4.exe实现功能1和功能4,在功能2和功能3文件夹中f4.exe实现功能2和功能3
战友:徐灿灿
功能1. 四则运算,支持出题4个数的四则运算题目,所有题目要求作者有能力正确回答 。
> f4
1+2*3+4=
?11
答对啦,你真是个天才!
1+2*3+5=
?11
再想想吧,答案似乎是12喔!
1+2/4-5=
?-3.5
答对啦,你真是个天才!
...(一共20道题)
你一共答对4道题,共20道题。
功能1的难点:
(1)对于表达式的计算,刚开始不知道使用什么方法来进行计算,通过在网上查找资料发现了数据结构的栈可以解决这个问题。于是将表达式求值分为了几个部分。
第一部分:将随机生成的表达式(中缀表达式)转换为后缀表达式。
网上资料:
将中缀表达式转换为后缀表达式:
与转换为前缀表达式相似,遵循以下步骤:
(1) 初始化两个栈:运算符栈S1和储存中间结果的栈S2;
(2) 从左至右扫描中缀表达式;
(3) 遇到操作数时,将其压入S2;
(4) 遇到运算符时,比较其与S1栈顶运算符的优先级:
(4-1) 如果S1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
(4-2) 否则,若优先级比栈顶运算符的高,也将运算符压入S1(注意转换为前缀表达式时是优先级较高或相同,而这里则不包括相同的情况);
(4-3) 否则,将S1栈顶的运算符弹出并压入到S2中,再次转到(4-1)与S1中新的栈顶运算符相比较;
(5) 遇到括号时:
(5-1) 如果是左括号“(”,则直接压入S1;
(5-2) 如果是右括号“)”,则依次弹出S1栈顶的运算符,并压入S2,直到遇到左括号为止,此时将这一对括号丢弃;
(6) 重复步骤(2)至(5),直到表达式的最右边;
(7) 将S1中剩余的运算符依次弹出并压入S2;
(8) 依次弹出S2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式(转换为前缀表达式时不用逆序)。
引用来自CSDN博客:云乐仙er[https://blog.csdn.net/qq_41668789/article/details/83017386]
于是我们从其中提取了博主的思想,稍加改动。首先定义一个ophead操作符的栈,还要定义一个存储输出的后缀表达式的字符串result,然后通过判断当前元素是否是操作符,如果是操作符,则与ophead操作符的栈顶进行优先级比较,如果小于栈顶优先级,则出栈,否则进栈;如果是操作数,则直接输出保存到后缀表达式的字符串中。
关键代码如下:
#将中缀表达式转化成后缀表达式
def Reverse(s):
ophead=[] #类似于操作符栈
result="" #以字符串的形式保存后缀表达式
rank={"+":1,"-":1,"*":2,"/":2} #定义字符串的优先级
for x in s:
if x in ["+","-","*","/"]: #判断当前元素是否是操作符
if(len(ophead)==0): #如果栈为空,操作符进栈
ophead.append(x)
elif(rank[ophead[-1]]>=rank[x]): #如果当前操作符的优先级小于ophead栈顶的元素优先级,则出栈
while(len(ophead)>0 and rank[ophead[-1]]>=rank[x]): #出栈,直到栈为空或者当前元素优先级大于栈顶元素
op=ophead.pop()
result=result+op
ophead.append(x) #当前元素的优先级大于栈顶元素的优先级,当前元素进栈
else: #如果当前元素的优先级大于ophead栈顶的元素优先级,则操作符进栈
ophead.append(x)
else: #如果当前元素是操作数
result=result+x
while(len(ophead)>0):#当ophead栈不为空时,输出栈,直到为空
op=ophead.pop()
result=result+op
return result
(2)第二部分:将中缀表达式转换为后缀表达式之后我们应当如何运算。
同样在刚刚云乐仙er的博客中找到了答案。
后缀表达式的计算机求值:
与前缀表达式类似,只是顺序是从左至右:
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 op 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果。
例如后缀表达式“3 4 + 5 × 6 -”:
1.从左至右扫描,将3和4压入堆栈;
2. 遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素,注意与前缀表达式做比较),计算出3+4的值,得7,再将7入栈;
3. 将5入栈;
4. 接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈;
5. 将6入栈;
6. 最后是-运算符,计算出35-6的值,即29,由此得出最终结果。
引用来自CSDN博客:云乐仙er[https://blog.csdn.net/qq_41668789/article/details/83017386]
首先我们先定义一个操作数的headlist栈,通过扫描所得的字符串,如果当前元素是操作数,则推进headlist中,否则是操作符,则连续出两次栈,然后对这两个操作数进行运算,运算的结果重新进入到headlist栈中,重复以上操作,直至栈为空。
关键代码如下:
#计算后缀表达式
def Countvalue(s):
headlists=[]
for i in s:
if i in ['+','-','*','/']:
b=float(headlists.pop())#栈顶元素出栈
a=float(headlists.pop()) #继续栈顶元素出栈
c=0
if i=='+':#两个操作数做四则运算
c=a+b
elif i=='-':
c=a-b
elif i=='*':
c=a*b
else:
c=a/b
headlists.append(c)#得到的结果压入栈中
else:
headlists.append(i)
return headlists[0]
(3)第三部分对于控制表达式的个数以及对于答案的判断进行设计
关键代码如下:
def main(argv):
#功能1或功能2:
if(len(argv)==1):
num=0
n=0
#for i in range(20):
while(n<20):
exp=Creat_exp()
print(exp+"=")
result_mid=Reverse(exp)
result=Countvalue(result_mid)
ans=input("?")
f=ans
if "-" in ans: #如果输入的是负数字字符串,isdigit()函数不能识别
f=ans[1:] #转化成正数数字字符串,再进行判断字符串是否是数字字符
if "." in ans: #如果输入的是小数数字字符串,isdigit()函数不能识别
f=f.replace(".","") #转化成整数数字字符串,再进行判断字符串是否是数字字符
if(f.isdigit()):
if float(ans) ==result:
print("答对了,你真是个天才!")
num+=1
n+=1
else:
print("再想想吧,答案似乎是",result,"喔!")
n+=1
else:
print("你输入的结果不是数字,请下一题重新输入数字")
print("你一共答对",num,"道题","一共20道题。")
功能1运行结果如下:

功能2. 支持括号
> f4
1+2*(3+4)=
?15
答对啦,你真是个天才!
(1+2)*3+5=
?11
再想想吧,答案似乎是14喔!
((1/2)-4)*5=
?-17.5
答对啦,你真是个天才!
...(一共20道题)
你一共答对4道题,共20道题。
功能2的难点:
(1)如何随机生成带有括号的表达式。
因为我们是具有四位操作数和三位操作符的表达式,对于括号的排列顺序不多,因此我们决定使用穷举法,先在草稿纸上写下所有的排列组合然后实现它。穷举所有表达式如下:

关键代码如下:
#随机生成表达式
#对于有括号的表达式,表达式中可能有一个括号,两个括号,所以有括号的随机表达式总共有10种
def Creat_exp():
op=["+","-","*","/"] #操作符
num1=int(r.uniform(1,10)) #随机生成1-9的数字 等同于r.randint(1,9)
num2=int(r.uniform(1,10))
num3=int(r.uniform(1,10))
num4=int(r.uniform(1,10))
nu1=r.randint(0,3) #randint(0,3)随机产生0,1,2,3
nu2=r.randint(0,2)
#下面是10种随机的有括号表达式
exp={1:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+op[nu1]+str(num4),
2:"("+str(num1)+op[nu2]+str(num2)+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
3:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(num3)+")"+op[nu1]+str(num4),
4:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(num3)+op[nu1]+str(num4)+")",
5:str(num1)+op[nu2]+str(num2)+op[nu2]+"("+str(num3)+op[nu1]+str(num4)+")",
6:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+"("+str(num3)+op[nu1]+str(num4)+")",
7:"("+"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
8:"("+str(num1)+op[nu2]+"("+str(num2)+op[nu1]+str(num3)+")"+")"+op[nu1]+str(num4),
9:str(num1)+op[nu2]+"("+"("+str(num2)+op[nu2]+str(num3)+")"+op[nu1]+str(num4)+")",
10:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+"("+str(num3)+op[nu1]+str(num4)+")"+")",
}
num5=r.randint(1,10)
exp1=exp[num5]
return exp1
(2)如何将带有括号的表达式(中缀表达式)转换为后缀表达式。
与功能1中的表达式转换相同,根据上述博主的资料。我们要考虑左括号和右括号的处理,左括号的优先级最低,右括号的优先级最高,对于当前元素是左括号,就直接进栈,如果是右括号,就直接出栈,直到遇到左括号为止,注意:这时左括号还在栈内,所以应该把它弹出。
关键代码如下:
#将中缀表达式转化成后缀表达式
def Reverse(s):
result="" #以字符串的形式保存后缀表达式
ophead=[] #类似于操作符栈
rank={"+":1,"-":1,"*":2,"/":2,"(":0,")":3} #定义操作符的优先级
for x in s:
if x in ["+","-","*","/","(",")"]: #判断当前元素是否是操作符
if (x=="("): #如果是左括号,直接进栈
ophead.append(x)
elif (x==")"): #如果是右括号,则出栈,直到遇到左括号停止
while(len(ophead)>0 and ophead[-1]!="("):
op=ophead.pop()
result=result+op #将出栈的元素保存至后缀表达式字符串中
ophead.pop() #把栈中的左括号弹出
elif(len(ophead)==0): #如果栈为空,操作符进栈
ophead.append(x)
elif(rank[ophead[-1]]>=rank[x]): #如果当前操作符的优先级小于ophead栈顶的元素优先级,则出栈
while(len(ophead)>0 and rank[ophead[-1]]>=rank[x]): #出栈,直到栈为空或者当前元素优先级大于栈顶元素
op=ophead.pop()
result=result+op
else: #如果当前元素的优先级大于ophead栈顶的元素优先级,则操作符进栈
ophead.append(x)
else: #如果当前元素是操作数
result=result+x
while(len(ophead)>0):#当ophead栈不为空时,输出栈,直到为空
op=ophead.pop()
result=result+op
return result
功能2的测试结果如下:
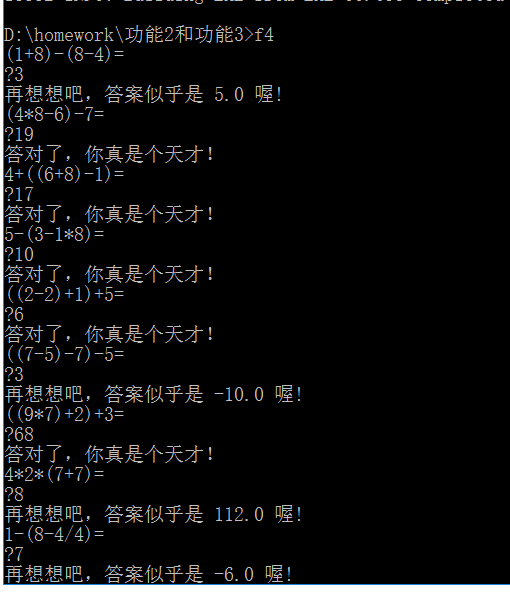
功能3. 限定题目数量,"精美"打印输出,避免重复
>f4 -c 3
1+2*(3+4)= 15
(1+2)*3+5= 14
((1/2)-4)*5= 17.5
功能2的难点:
(1)如何规范输出。
使用的是python中的函数定义的输出规范,关键代码如下:
print(ex.ljust(30),result) #规范输出,使用了ljust()函数,该函数作用是字符靠左边,右边空多余的空格
(2)如何判断输入的个数符合正整数数字。如何与功能2区分。
1.在python中有专门的判断是否字符串全部为数字的函数 “isdigit()”,当输入负数或者是小数时字符串中出现了数字以外的字符,因此我们使用此函数来进行判断。
2.通过对命令行参数的不同来进行辨别可以与功能2区分开来。
关键代码如下:
def Input(s): #判断是否是正整数,isidgit()函数是不能识别小数和负数字符串
if(s.isdigit()):
return int(s)
else:
return 0
#功能3
elif(sys.argv[1]=="-c"):
a=Input(sys.argv[2]) #获取题目个数
if(a>=1):
num=0
n=0
#for i in range(20):
while(n<a):
exp=Creat_exp()
ex=exp+"="
result_mid=Reverse(exp)
result=Countvalue(result_mid)
print(ex.ljust(30),result) #规范输出,使用了ljust()函数,该函数作用是字符靠左边,右边空多余的空格
n+=1
else:
print("题目数量必须是正整数。")
功能3测试结果如下:
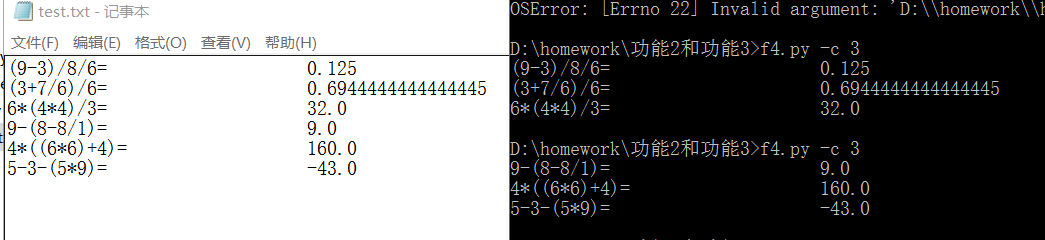

功能4. 支持分数出题和运算
国庆节后,你终于又回到美丽优雅并且正常的东北师范大学净月校区,在去食堂的路上偶遇你心目中的女神 (或男神,请自行替换)。她说,"哎呀,这跟我们《构建之法》课上的题目要求一样啊,真是巧合。"
"不要客气,代码拿去!反正我也没用。"你说,"如果有需求变更或扩展,尽管找我。"
你伏笔埋得不错。女神马上说,"对啊,有一点儿点儿不一样,你午饭时间加加班帮我改出来吧。"
她的题目还要求支持分数运算,你不禁想到了功能1中你特意规避了一些题目不出。她想要的是下面的样子:
f4 -c 3
1/3+2/3+1+1= 3
1/2+2/3+1+2= 4 1/6
7/5+3/4*2-3 -1/10
你想到越难的题目就越能表现你的能力,欣然应允了,转身跑向实验室,路上就开始给师兄打电话。背后传来女神的声音,"提示1:别忘了约分。提示2:带分数,即 一又二分之一 表示 1 1/2。"
完成这个功能,女神对你的青睐+200。
功能4难点:如何对分数表达式进行运算。
对于分数的运算我们尝试接着使用后缀表达式来继续计算,但是多次尝试后(可能是我们能力有限)并没有解决这个问题,然后我们就去网上查找了资料找到了相关资料,在python中有fractions模块和eval()函数,fractions模块中有一个Fraction()函数。
Fraction函数支持分数运算,输入参数可以是一对整数,一个分数,一个小小数或者一个字符型数字。
1.Fraction(分子=0, 分母=1)
默认参数分子为0,分母为1。
输入两个整数(分别作为分子、分母),返回两数约分后的结果。
2.Fraction(浮点数)
输入浮点数,会返回该数的分子分母形式。
3.Fraction(分数)
输入分数,会返回该数的分子分母形式。
4.Fraction(字符串)
输入字符型数字,会返回该数的分子分母形式
eval()函数的作用 是将字符串str当成有效的表达式来求值并返回计算结果。
资料如下:
fraction函数的详细用法参考链接:[https://blog.csdn.net/u012949658/article/details/105837120]
eval函数的详细用法参考链接:[https://www.jianshu.com/p/b2d3a77f76f8]
关键代码如下:
def count(s):
result=f(eval(s)).limit_denominator(1000) #利用eval函数计算字符串表达式的值,并且分子分母均小于1000
return str(result)
(2)如何设计有分数且带有括号的表达式。
我们尝试了寻找了一些资料和验证了自己的想法发现没有好的方法来设计于是我们决定采用穷举法来设计表达式,我们列举的表达式有32种。
关键代码如下:
def Creat_exp2():
op=["+","-","*","/"] #操作符
num1=int(r.uniform(1,10)) #随机生成1-9的数字 等同于r.randint(1,9)
num2=int(r.uniform(1,10))
num3=int(r.uniform(1,10))
num4=int(r.uniform(1,10))
nu1=ri(0,3) #randint(0,3)随机产生0,1,2,3
nu2=ri(0,2)
#下面是32种随机的有括号且有分数的表达式
exp={1:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+op[nu1]+str(num4),
2:"("+str(num1)+op[nu2]+str(num2)+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
3:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(num3)+")"+op[nu1]+str(num4),
4:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(num3)+op[nu1]+str(num4)+")",
5:str(num1)+op[nu2]+str(num2)+op[nu2]+"("+str(num3)+op[nu1]+str(num4)+")",
6:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+"("+str(num3)+op[nu1]+str(num4)+")",
7:"("+"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
8:"("+str(num1)+op[nu2]+"("+str(num2)+op[nu1]+str(num3)+")"+")"+op[nu1]+str(num4),
9:str(num1)+op[nu2]+"("+"("+str(num2)+op[nu2]+str(num3)+")"+op[nu1]+str(num4)+")",
10:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+"("+str(num3)+op[nu1]+str(num4)+")"+")",
11:"("+str(f(ri(1,10),ri(1,10)))+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+op[nu1]+str(num4),
12:"("+str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+")"+op[nu1]+str(num3)+op[nu1]+str(num4),
13:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num4),
14:"("+str(num1)+op[nu2]+str(num2)+")"+op[nu1]+str(num3)+op[nu1]+str(f(ri(1,10),ri(1,10))),
15:"("+str(f(ri(1,10),ri(1,10)))+op[nu2]+str(num2)+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
16:"("+str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num3)+")"+op[nu1]+str(num4),
17:"("+str(num1)+op[nu2]+str(num2)+op[nu1]+str(f(ri(1,10),ri(1,10)))+")"+op[nu1]+str(num4),
18:"("+str(num1)+op[nu2]+str(num2)+op[nu1]+str(num3)+")"+op[nu1]+str(f(ri(1,10),ri(1,10))),
19:"("+str(f(ri(1,10),ri(1,10)))+op[nu2]+str(f(ri(1,10),ri(1,10)))+")"+op[nu1]+str(num3)+op[nu1]+str(num4),
20:"("+str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+")"+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num4),
21:str(f(ri(1,10),ri(1,10)))+op[nu2]+"("+str(f(ri(1,10),ri(1,10)))+op[nu2]+str(num3)+")"+op[nu1]+str(num4),
22:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(f(ri(1,10),ri(1,10)))+")"+op[nu1]+str(f(ri(1,10),ri(1,10))),
23:str(f(ri(1,10),ri(1,10)))+op[nu2]+"("+str(f(ri(1,10),ri(1,10)))+op[nu2]+str(num3)+op[nu1]+str(num4)+")",
24:str(num1)+op[nu2]+"("+str(num2)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10)))+")",
25:str(f(ri(1,10),ri(1,10)))+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10))),
26:str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10))),
27:str(f(ri(1,10),ri(1,10)))+op[nu2]+str(num1)+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10))),
28:str(f(ri(1,10),ri(1,10)))+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num1)+op[nu1]+str(f(ri(1,10),ri(1,10))),
29:str(f(ri(1,10),ri(1,10)))+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num1),
30:str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num1),
31:str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num1)+op[nu1]+str(num1),
32:str(num1)+op[nu2]+str(f(ri(1,10),ri(1,10)))+op[nu1]+str(num1)+op[nu1]+str(f(ri(1,10),ri(1,10))),
}
num5=ri(1,32)
exp1=exp[num5]
return exp1
(3)如何输出带分数以及对于负带分数的处理。
这个地方我们卡了一下,两个人都想着直接以结果的形式直接输出,纠结了很久。后来发现了其实我们可以在输出的时候对函数的运算返回值进行一些处理,来规范其格式。这样会好很多,在对带分数输出时,同类似也可以对负带分数进行处理。同样的思想直接解决掉两个问题。
关键代码:
result=count(exp)
if "/" in result: #处理分数部分
1234t,v=map(int,result.split("/")) #t为分子,v为分母
if(t>0 and t>v): #简化成正带分数
c=t//v #整除
d=t%v
e=v
print(ex.ljust(30),"%d %d/%d" %(c,d,e)) #输出带分数形式
elif(-t>v): #简化成负带分数
# print(t,v)
c=t/v
d=-t%v
e=v
print(ex.ljust(30),"%d %d/%d" %(c,d,e)) #输出带分数形式
else:
print(ex.ljust(30),result) #规范输出,使用了ljust()函数,该函数作用是字符靠左边,右边空多余的空格
else:
print(ex.ljust(30),result) #规范输出,使用了ljust()函数,该函数作用是字符靠左边,右边空多余的空格
功能4测试结果如下:
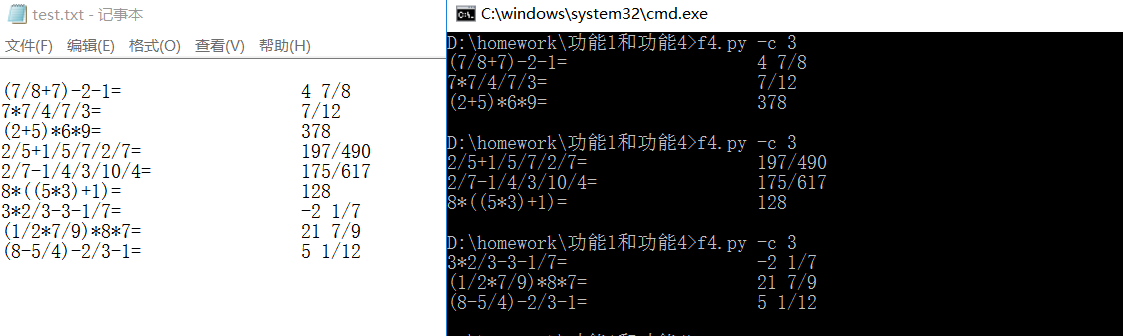
结对编程体会
(1)对于工程开始时我们先讨论了一次使用语言以及算法的情况,让我体会挺深,应当多多学习一些语言,抓住一门精通。
(2)逆波兰式的算法思路。长时间没有接触过数据结构导致了我们在对中缀转后缀时出现了各种各样的问题,之后不得不按照逻辑结构推算了一遍方才解决。
(3)对于操作符的优先级包括“=,- ,*,/,(,)”的优先级进行合理的分配以及设计优先级的代码实施进行了讨论。
(4)在随机生成括号表达式时,我们两个通力合作将所有的情况列举出来,然后根据数学的结合律等排除掉重复的情况,穷举出所有的表达式。
(5)在此次结对编程中,我体会到了代码风格规范以及代码设计规范在今后工作中的重要性,一个项目不仅仅是你自己来完成,当你的代码不符合规范时将会带来极大的不便项目越复杂问题越大。而且通过此次结对编程让我对于项目的合作编程有了一个很大的感触,每一个都有自己的想法有自己的思路,应当多多吸取别人的想法有可能会带来意想不到的惊喜。
