该选择多少个主成分
群体结构(population structure),或者说群体分层(population stratification),是由于个体之间非随机交配而导致的群体中亚群之间等位基因频率的系统差异。这种系统差异,是全基因组关联研究(GWAS)中影响非常大的混淆变量,可以造成非常大的假阳性。
举个简单的模拟例子 [1],当 GWAS 中不存在群体分层时,得到的结果会是比较真实可靠的:
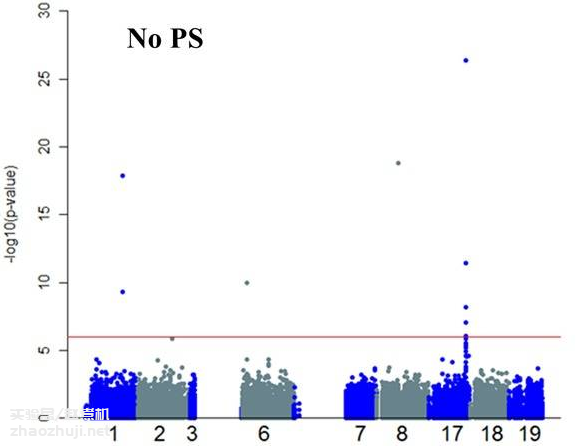
当样本存在一定程度的群体分层现象时,会出现一些假阳性信号:
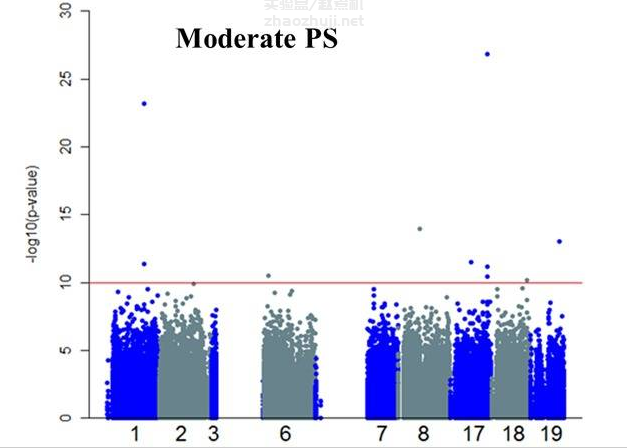
当群体分层现象非常严重时,bonferroni correction 校正也没什么用,大量位点都会超过 bonferroni correction 的阈值:

为了尽量降低群体结构的影响,通常会先对基因组进行主成分分析(PCA),然后在做 GWAS 时会加入主成分(principal components, PCs)作为协变量。
但问题就来了,该选择多少个主成分去校正群体结构?PCA 个数的选择对结果影响很大。如果选择的个数太少,无法有效校正群体结构,假阳性仍然会很大。但如果选择的个数太多,会影响 GWAS 的 power。 下面就说说常见的几种方法。
直接选取前 k 个主成分
最简单直接的方法就是人为选择前 k 个 PCs 作为协变量,比如直接选取前 5 个或者前 10个。早期的文献通常推荐使用前 10 个 PCs作为协变量,校正群体结构 [1]。
不过,这种方法过于简单粗暴。在人群数量和样本数量快速增长、一个 GWAS 能达到几万人甚至几十万人的今天, 这样的粗暴方法往往并不足以校正群体结果。
所以,这种方法虽然简单,但并不推荐。
基于 PCA 散点图或者 ANOVA
如果要更为可靠地选取 PCs 数量,可以绘制用 eigenvector 绘制散点图,选择可以将群体有效分开前 k 个 的主成分。比如下面这张图,前两个 PCs 可以将 3 个群体分开,而 PC3、PC4 无法将三个群体分开。这时,选择 PC1 和 PC2 作为 GWAS 的协变量就足够了。如果强行把 PC3 和 PC4 也加进去,反而会带来很大的 bias。
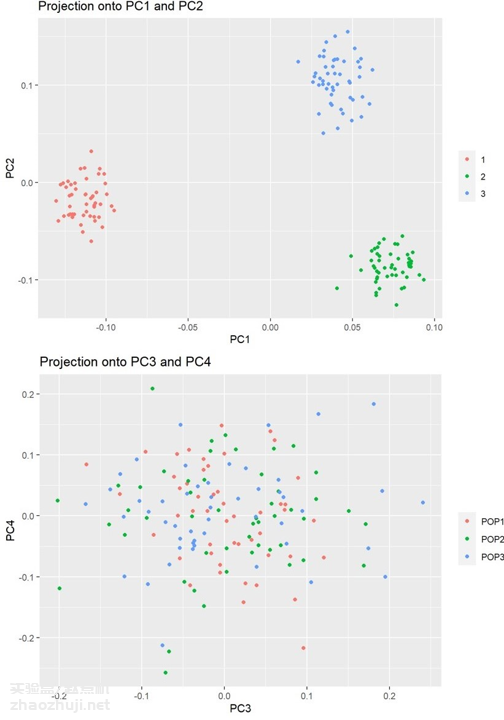
进行 PCA 并且画图的操作过程可看看 https://www.biostars.org/p/335605/ 这篇教程,它以 1000 Genomes Phase III 数据为例手把手教学。中文教程, 也可以看看 https://www.cnblogs.com/chenwenyan/ 博客。
觉得画图不够客观,或者太过麻烦,如果知道群体的个数的话也可以对主成分进行 ANOVA 分析,检验主成分在不同人群中是否显著,选择显著的前 k 个主成分。
twstats 方法(推荐)
第二种画图的方法观察起来还是有些主观,如果不能很好定义人群,ANOVA 的方法也不太好用。是否有更好的方法?
这里推荐 Patterson 在 2006 年发表的 EIGENSTRAT 文章中的 twstats 方法(compute number of statistically significant principal components) [2]。它基于 Tracy–Widom statistics,对各个主成分进行显著性检验。在模拟结果中,Tracy–Widom statistics 的显著性检验结果与 ANOVA 比较吻合,可靠性不错。

这种方法集成在 EIGENSOFT 的 twtable 中。Plink 或者 EIGENSTRAT 的 PCA 结果可直接用来计算:
# 利用 Plink 计算 PCA,输出前 50 个主成分
plink --bfile yourfile --pca 50 --out yourfile_pca
# 下载解压,如果下面的网址无法下载,可以试试 https://storage.googleapis.com/broad-alkesgroup-public/EIGENSOFT/EIG-6.1.4.tar.gz
wget https://data.broadinstitute.org/alkesgroup/EIGENSOFT/EIG-6.1.4.tar.gz
tar xzvf EIG-6.1.4.tar.gz
# 利用 twstats 进行显著性检验
/bin/twstats -t twtable -i yourfile_pca.eigenval -o yourfile_pca_number
在结果输出文件中选择 P < 0.05 的前 k 个主成分:
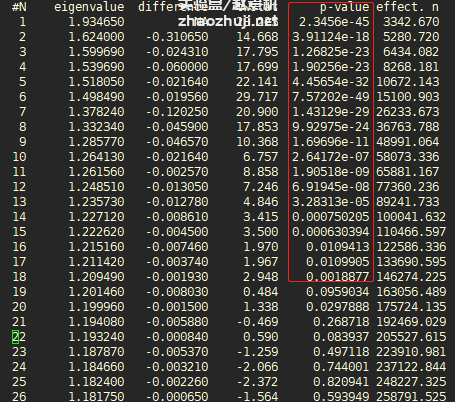
不过,用 twstats 评估显著性时要注意:The twstats program assumes a random set of markers, and should not be used on data sets of ancestry-informative markers, as admixture-LD may violate its underlying assumptions.。也就是说,如果你的基因型数据都是 ancestry-informative markers,就不能用这种方法。
基于可解释方差(推荐)
除了基于 Tracy–Widom statistics 检验主成分的显著性外,还可以根据每个主成分的可解释方差计算。一般,选取累计解释 80-90% 的前 k 个主成分就足够。Plink、GCTA 等工具不能输出各个主成分的可解释方差,要这个信息的话可以用 vcfR、SNPRelate、bigsnpr、pcadapt 等 R 包。
SNPRelate 的并行计算速度比较快,以它为例,计算 PCA 并且得到可解释方差:
# from shiyanhe and zhaozhuji.net
# 从 Bioconductor 安装 SNPRelate 包和它依赖的 gdsfmt 包
if (!requireNamespace("BiocManager", quietly=TRUE))
install.packages("BiocManager")
BiocManager::install("gdsfmt")
BiocManager::install("SNPRelate")
# 加载 gdsfmt 和 SNPRelate 包
library(gdsfmt)
library(SNPRelate)
# 输入 PLINK 文件路径
bed.fn <- "/your_folder/your_plink_file.bed"
fam.fn <- "/your_folder/your_plink_file.fam"
bim.fn <- "/your_folder/your_plink_file.bim"
# 将 PLINK 文件转为 GDS 文件
snpgdsBED2GDS(bed.fn, fam.fn, bim.fn, "test.gds")
# 读取 GDS 文件
genofile <- snpgdsOpen("test.gds")
# 根据 LD 过滤 SNPs,阈值根据需要设定
set.seed(1000)
snpset <- snpgdsLDpruning(genofile, ld.threshold=0.2)
# 选择 SNP pruning 后要保留的 SNP
snpset.id <- unlist(unname(snpset))
# 计算 PCA,num.thread 是并行的线程数
pca <- snpgdsPCA(genofile, snp.id=snpset.id, num.thread=10)
# 以百分比形式输出 variance proportion
print(pca$varprop*100)
当然,也可以绘制碎石图( scree plot)来观察:
# 绘制前 30 个主成分的碎石图
# from shiyanhe and zhaozhuji.net
library(ggplot2)
K= 30
qplot(x = 1:K, y = (pca$varprop[1:K]), col = "red", xlab = "PC", ylab = "Proportion of explained variance") +
geom_line() + guides(colour = FALSE) +
ggtitle(paste("Scree Plot - K =", K))
这样就可以画出碎石图:
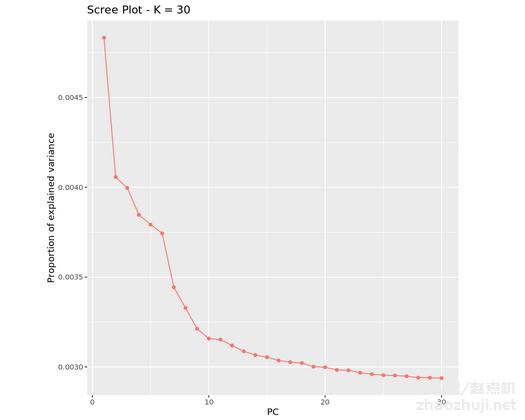
总结
总的来说,这里推荐第三种方法 twstats 和第四种基于累计可解释方差的方法。在实际应用中,建议同时结合这两种方法。首先用 twstats 方法计算各个主成分显著性,再计算各个主成分的可解释方差,然后选取 P 值显著且累计可解释方差在 80-90% 的前 k 个主成分。这样可以让结果更为可靠,选择更恰当的主成分个数。
参考:
[1] Zhao H, Mitra N, Kanetsky P A, et al. A practical approach to adjusting for population stratification in genome-wide association studies: principal components and propensity scores (PCAPS)[J]. Statistical applications in genetics and molecular biology, 2018, 17(6).
[2] Patterson N, Price A L, Reich D. Population structure and eigenanalysis[J]. PLoS genet, 2006, 2(12): e190.
[3] https://www.biostars.org/p/126274/
[4] https://www.biostars.org/p/305469/
[5] https://www.biostars.org/p/335605/
[6] https://www.cnblogs.com/chenwenyan/
[7] twstats文档:https://github.com/chrchang/eigensoft/blob/master/POPGEN/README
